基金项目:国家自然科学基金(11101023)
作者简介:江凡(1991—),男,硕士,研究领域为液体推进系统动力学与仿真
(School of Astronautics, Beihang University, Beijing 100191, China)
thermodynamic calculation; chemical equilibrium flow; total energy conservation; turbine test rig system; numerical simulation
在推进剂燃烧的建模上,传统的热力计算方法一般基于总焓守恒求解定压绝热燃烧温度和平衡组分,不能考虑壁面传热;在燃气流动的建模上,通常采用的冻结流模型认为本地的组分及热物理性质与燃烧室瞬时一致,忽略了这些参数因来流气体与本网格滞留气体掺混带来的随时间的缓变效应。提出了一种新颖的可以考虑壁面传热的基于总能量守恒的化学平衡流计算方法,运用Fortran2008语言,采用面向对象编程方法建立了化学平衡流燃气发生器管道的模块化仿真模型,并将该模型应用到一个包含42个组件的涡轮试验台气路系统的建模与仿真中。与早期模型仿真结果及试验数据的对比发现,新模型的仿真结果有一定改进,更加接近试验数据。
As for the modeling of propellant combustion, the traditional thermodynamic algorithms generally use the total enthalpy conservation to solve constant-pressure adiabatic combustion temperature and equilibrium compositions, which can not consider the wall heat transfer. As for the modeling of combustion-gas flow, the frozen-flow model is usually employed with the assumption that local compositions and the thermophysical properties are instantaneous consistent with those in the combustion chamber, which ignores the slowly-varying effect of these parameters caused by the mixing process of the incoming flow and the residual gas in local grid. In view of the abovementioned weaknesses, a novel chemical equilibrium flow algorithm based on total energy conservation is proposed, which can consider the wall heat transfer. By using Fortran 2008 language and object-oriented programming method, a modular simulation model of chemical equilibrium flow gas generator pipe is established, and is applied to the modeling and simulation of a turbine test rig gas
系统仿真[1-7]是研究发动机工作特性的重要方法,目前NASA的推进系统数值仿真NPSS(Numerical Propulsion System Simulation)项目代表着当今发动机系统仿真的最高水平[1-2]。Amesim[3],GFSSP[4]及Matlab/Simulink[5-6]等系统仿真软件在发动机系统仿真领域应用较多,为了在系统仿真的准确性和运算速度之间做到合理的平衡,通常采用一维甚至零维的仿真模型。
在发动机燃烧室及喷管内流场仿真计算中,热力计算[8-11]是一种重要方法,流动计算中冻结流模型[12-14],化学非平衡流模型[15-17]应用较多。
传统的热力计算方法一般采用总焓守恒求解,不能考虑传热。例如高玉闪使用布林克莱法对氢/氧推进剂进行热力计算,确定各组分的摩尔数和燃烧产物温度[9]。Kayadelen采用化学平衡常数法研究CαHβOγNδ类型燃料水喷注燃烧现象,并基于总焓守恒求解绝热燃烧温度[10]。Kady在二维的N-S方程中,采用化学平衡常数法基于总焓守恒求解燃烧室温度[11]。
吕翔针对以H2O2(L)/JP-10(L)为推进剂的RBCC发动机,建立了火箭燃烧室热力计算模型,并采用冻结流假设进行喷管热力计算[14]。汪球采用5组分17步反应机理,研究高焓激波风洞中典型状态下气流的热化学非平衡流动特性[15]。Wei采用Ar元素的相关反应,研究Ar等离子在喷管非平衡流动中的膨胀过程[16]。
冻结流模型认为组分及物性不变,当地网格的组分和热物理性质参数与上游瞬时一致,忽略了这些参数因来流气体与本网格滞留气体掺混带来的随时间的缓变效应;化学非平衡流从化学反应动力学出发,考虑反应机理,虽然更加精细,但是会带来刚性问题,在系统级仿真中使计算效率大大降低,并且其准确性取决于所采用反应机理的详细程度和适用范围,例如高温机理无法模拟低温燃烧。相对于上述2种模型,平衡流[18]模型燃烧产物的组分摩尔分数及热物性参数由当地网格参数求解,且不会明显降低计算效率。
运用模块化建模思想[7,12],文献[13]针对涡轮试验台气路系统建立了包含42个组件的数值仿真模型,加热器及其出口段(燃烧装置,以下简称加热器)燃烧区采用壁面绝热的基于总焓守恒的热力计算方法,流动区采用冻结流模型。加热器总温的动态仿真结果与试验数据一致,但加热器后续管道中的管流总温明显高于试验数据。
针对以往研究中的不足,本文提出了一种基于总能量守恒的热力计算方法,并从平衡流物理化学实质出发,进一步提出了一套新颖的基于总能量守恒的化学平衡流计算方法,采用该方法改进文献[12-13]中的加热器模型,并通过与试验数据的对比,验证新方法的有效性。
图1所示为由42个组件组成的涡轮试验台气路系统的仿真模型,模块化建模[13]时划分为2个流体源(FS1-2),20个气体管道(GP1-20),5个气体容积(GVol1-5),1个气体掺混器(GMA1),9个气体阀门(GV1-9),1个气体喷注器(GI1),1个气体稳定器(GSA1),1个化学平衡流燃气发生器管道(CEFGGP1),1个气涡轮(GTurbo1)和1个转子(Rotor1)。Tt13/Tt14(2个传感器在同一横截面不同位置测量总温,后面类似)、Tt51/Tt52及Tt33/Tt36分别为加热器下游、放气旁路管道GP16及主路测量段管道GP17总温测点。
加热器(CEFGGP1)、管道GP16、GP17的长度(单位:m)、外径、壁厚(单位:mm)如图1所示,其他元件结构参数参见文献[13],管道类元件每100 mm划分一个网格,气体阀门与气体容积元件划分为2个标准网格,总长200 mm。FS1和FS2分别为入口流体源和出口流体源。其中,管道GP15,阀门GV7及管道GP16组成放气旁路,管道GP17,阀门GV8及管道GP18组成涡轮主路工作段为涡轮输送高温高压燃气,最终带动转子做功。
试验和算例设置、调节时序情况参见文献[13],仿真时给定一个初始流场和温度场分布,待冷流稳定后,10 s时刻在加热器中(CEFGGP1)点火,整个仿真过程持续260 s,重点关注燃烧装置在20~260 s的仿真结果。FS1~2两个流体源边界条件采用试验测量数据,即燃油质量流量Qmf、大气压强p0的时间-参数点列形式的试验测量数据。整个系统工作状况随阀门开度及流体源边界条件而变化。本文针对其中的加热器(CEFGGP1)开展研究工作。
平衡流模型假设认为在流动过程中,物质化学反应速率无限快,燃烧物质时刻处于一种组分和能量的化学平衡状态。
加热器型号为BK-1型单管燃烧室,分别以空气、RP-3煤油为氧化剂和燃料。如图2所示为根据加热器建立的化学平衡流燃气发生器管道模块的网格图,将加热器划分为掺混点火区与流动燃烧区。氧化剂和燃料进入掺混点火区发生化学反应,然后燃烧物质流入到流动燃烧区。
图2 化学平衡流燃气发生器管道有限体积网格
Fig.2 Finite control volume grids of chemical equilibrium flow gas generator pipe
相较于文献[12-13]中的加热器模型,基于总能量守恒的平衡流模型有以下不同的假设:
1)掺混点火区采用总能量微分方程代替压强微分方程,燃烧过程不再是绝热的,可以考虑壁面传热;
2)流动燃烧区组分和物性不再冻结不变,而是随当地网格的混合比等状态参数而变化。
这2点假设的不同会带来新模型中温度及压强算法的不同。
掺混点火区能量方程:
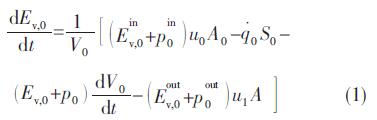
相较于文献[12-13]中,式(1)有传热项 。
。 为掺混点火区入口空气和煤油总能量,包含空气和煤油的化学能,并分别采用空气、煤油入口端温度Ta,o,Ta,f计算空气和煤油的焓值:
为掺混点火区入口空气和煤油总能量,包含空气和煤油的化学能,并分别采用空气、煤油入口端温度Ta,o,Ta,f计算空气和煤油的焓值:

式中:ΔhTs ,is为推进剂的标准生成焓;cp,is为定压比热;Ts为基准温度。
连续方程:
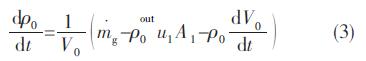
式中m.g为燃气质量生成率。
混合物分数方程:
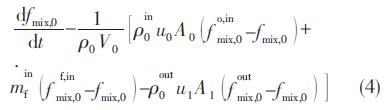
其中
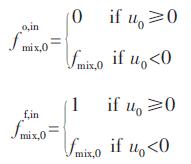
流动燃烧区能量方程:

连续方程:i=1,…,n
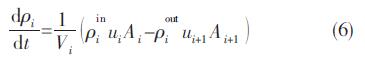
混合物分数方程: i=1,…,n
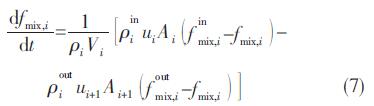
动量方程: j=1,2,…,n+1

其中
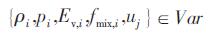
式中边界参数Varin和Varout采用迎风格式。
速度:
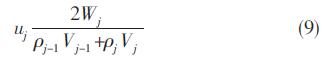
网格i的单位体积总能量:
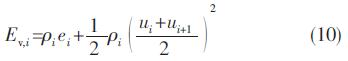
单位质量的内能:

理想气体状态方程:

平均气体常数:

式中:nmolg,j为i网格1 kg物质的气体总摩尔数;R0为通用气体常数。内能、焓和总能量都考虑物质化学能。
联立式(10)~式(12)得:
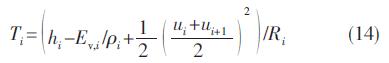
其中hj为i网格所有组分的焓值总和:
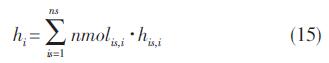
式中:nmolis,i为i网格1 kg物质中组分is的摩尔数;ns为组分总数;his,i为1摩尔第is种组分的焓值(J/mol),是温度的单值函数,可由NASA七系数或九系数拟合公式得到[18]。
上述方程为常微分方程的初值问题,沿时间推进求解时步骤如下:
1)流动燃烧区常微分方程变量Ev,i,ρi,fmix,及Wj由式(5)~式(8)沿时间积分求解,uj由式(9)得到,这些参数对于本时层的代数方程求解来说成为定值。对于代数方程变量来说:hj是温度Tj和组分摩尔数nmolis,i的函数,而需要热力计算得到的nmolis,i;Ri又是fmix,i,pi的函数,因此需联立式(12)~式(15)迭代求解温度Ti。掺混点火区Ev,0,ρ0及fmix,0 由式(1)、式(3)及式(4)沿时间积分求解,u0由上游组件决定,其他步骤相同。
2)不论冷流、热流,均在式(14)中采用二分法求解i网格的温度Ti,二者不同之处在于焓值hi和组分数nmolis,i的计算。
热流时选取试算温度Tmiddle,在平衡组分初值库中,由当前时层混合比rof=1/fmix,i-1预估Tmiddle下平衡组分初值nmolis,i,由式(12)和式(13)得到试算压强pmiddle,采用基于化学平衡常数法或最小吉布斯自由能法的热力计算方法求解Tmiddle和pmiddle下平衡组分值,由式(15)计算燃烧混合气的焓hi,并采用式(13)更新Ri,最终根据式(14)采用二分法迭代求解温度Ti。
冷流时,忽略煤油对冷流的贡献,只考虑空气流动。视空气为一定比例的Ar、O22及N2三种组分的混合物,则nmolis,i和nmolg,i为定值,因此hi是温度的单值函数,联立式(13)和式(15),最终根据式(14)采用二分法迭代求解温度Ti。
3)得到网格温度Ti后,由式(12)求压强pi。
4)热流时由热力计算得到最终的燃烧产物组分数及热物性参数;冷流时,各物质组分即为空气组分,物性参数由上游相连组件参数赋值。
文献[13]采用Fortran95语言和面向过程的编程方法,建立了涡轮试验台气路系统的模块化仿真模型。其中加热器模型燃烧区采用壁面绝热的基于总焓守恒的热力计算模型,流动区采用基于总能量(不包含化学能)守恒的冻结流模型,传热模型采用文献[19]在圆柱坐标系下建立的一种计算管壁传热的轴对称二维有限体积模型。此方案称为旧方案。
本文采用Fortran2008语言编程,将试验台系统所涉及的主要模块面向对象化,并采用新的平衡流模型对加热器进行改进,掺混点火区和流动燃烧区采用基于总能量(包含化学能)守恒的平衡流模型并考虑传热,此方案称为新方案。
加热器和气体管道壁面传热采用轴对称二维传热模型,气体阀门、喷注器、气体稳定器及气涡轮为径向一维传热模型,气体容积为零维传热模型,气体掺混器为绝热模型。
在编程过程中还进行了其他许多改进以优化代码,例如改进了热力计算过程中确定温度的二分法方案,基本思想是采用上一时层的温度确定本时层温度二分法求解初值,在收敛精度提高到0.01 K的情况下反而减小了二分法迭代步数。数值试算表明,面向对象化和二分法改进使得计算速度提高了约20%。
图3 加热器下游总温仿真结果与试验数据的对比
Fig.3 Comparison of heater-downstream total temperature simulation results with test data
如图3~图5所示为采用化学平衡常数法的2种方案仿真结果与3个测点处试验数据的对比。
图3中nT为转子转速,GGP-Tt(n/2)、CEFGGP-Tt(n/2)分别为旧方案和新方案加热器下游中间网格处总温。图4中GP16-Tt(n/2)、GP16-Tt(n-1)分别为管道GP16中间网格与末端网格总温。图5中以此类推。
图4 放气旁路总温仿真结果与试验数据的对比
Fig.4 Comparison of bypass measurement-section total temperature simulation results with test data
图5 主路测量段总温仿真结果与试验数据的对比
Fig.5 Comparison of main-line measurement-section total temperature simulation results with test data
根据涡轮试验台气路系统运行工况,在30 s,120 s及260 s分别截取3个测点的总温数据,并与试验数据进行对比,如表1和表2所示。
从表1可以看出,新方案的加热器下游总温相对于旧方案有一定下降,在30 s,120 s及260 s时,分别下降12.94 K,12.31 K及12.4 K。尽管如此,从图3可以看出,2种方案的总温仿真曲线整体上都落在了加热器下游同一测点2个传感器Tt13和Tt14测得的总温曲线的范围内,说明新旧方案在加热器下游总温计算上都与试验相符。
加热器总温下降一方面是掺混点火区采用式(1)求解总能量,在计算空气、煤油焓值时,采用加热器入口温度计算;而旧方案中,统一采用煤油初温Tinit计算,Tinit=282 K是煤油实测温度的平均值。可见采用加热器入口温度更加接近实际,空气入口温度在仿真涉及的260 s过程中约为270 K,相对于Tinit小12 K,引起仿真得到的加热器总温下降约10 K。另一方面,掺混点火区考虑壁面传热,导致燃气总温又下降2~3 K。最终加热器总温相较原始方案约有12~13 K的下降。
表2 新旧方案总温仿真结果与试验数据的对比结果
Tab.2 Comparison of total temperature simulation results of new and old cases with test data
加热器总温下降引起了后续管道总温的下降,如表1所示,在这3个时刻点,新方案放气旁路管道GP16总温相对于旧方案分别有8.06 K,7.8 K及9.41 K下降;主路测量段管道GP17总温则分别有2.49 K,3.15 K及8.91 K下降。
从图4可以看出,与试验数据总温Tt51和Tt52对比,新方案中放气旁路总温仿真结果更加接近试验曲线。如图5显示与试验数据总温Tt33和Tt36对比,新方案中主路测量段总温仿真结果更加接近试验曲线;只是在62.9 s时刻GV8阀门开启后,在约70~150 s时间段内,仿真结果总温突然上升,试验总温缓慢上升,二者趋势仍不一致。分析原因为:鉴于当前算例中后续组件仍然采用冻结流模型,组分及热物理性质参数根据加热器末端网格计算结果直接赋值,导致后续组件网格中的这些参数是突变的,而实际情况应该是物性随时间缓变的。后续针对该差异,进一步细化加热器后续管道模型,更好地描述气路系统中温度沿流动方向的分层现象。
通过上述分析与比较,得出以下结论:
1)新方案加热器掺混点火区分别采用空气、煤油入口端温度代替原始方案中的煤油初温计算空气和煤油焓值,更加接近物理化学实际,且导致加热器下游总温下降约10 K。
2)加热器掺混点火区采用基于总能量守恒的平衡流模型,相对于传统基于总焓守恒的方法,物理意义更加接近实际。其中,考虑壁面传热导致加热器下游总温计算结果较原始方案降低2~3 K。
3)加热器下游总温降低,导致后续组件中放气旁路总温、主路测量段总温仿真曲线也整体降低,更加接近试验曲线。
4)通过大量的文献调研,尚未发现考虑壁面传热的基于包含化学能总能量守恒的类似方法,因此本文提出的方法具有一定的新颖性,在燃烧室及燃气流动装置建模与仿真领域具有一定的工程应用价值。
5)后续考虑对加热器后续管道进行平衡流模型改造,以期能够实现当地网格组分及物性参数的缓变效应,更好地描述涡轮试验台气路系统中温度沿流动方向的分层现象。