滑动轴承具有结构简单、承载能力强、噪声小、寿命长等诸多优点[1－2]，广泛应用于航空、航天、石化、电力等各类旋转机械中。油膜失稳是滑动轴承转子系统最常见的故障之一。由于转子失稳具有突发性，且失稳后振动量级在短时间内会急剧增大，可能对轴系及支承系统造成极大的破坏，因此在升高速和超速运行过程中，除进行轴系振动、轴承工作状态及轴承受力监测和分析外，还必须进行专门的稳定性分析。随着旋转机械技术指标要求的不断提高，结构简单、重量轻、大长细比已成为高速轴系结构发展的趋势，这种发展趋势必然造成转子临界转速降低、轴系不稳定区扩大，因而更容易发生油膜失稳[3－4]。本文在理论分析的基础上，结合试验转子的升高速运行过程，对滑动轴承-转子系统的稳定性进行了研究。

考虑如图1所示的转子系统：一无质量的弹性轴段左端支承于刚度无限大的轴承上，右端有集中质量 ，该集中质量处安装有滑动轴承。滑动轴承油膜在集中质量M质心处产生的径向等效刚度为K。轴颈和轴承壳体间充满粘性润滑油，轴颈的高速运转会带动润滑油沿周向运动，其运动过程及机理十分复杂，为了说明问题的方便，对润滑油的运动过程进行简化。假定润滑油周向运动平均速度v^-与轴颈转速Ω满足式(1)的关系^[5]：

流体周向平均速度系数λ∈(0, 0.5)为一常数，其值与轴承结构参数及运行工况密切相关，r 为集中质量M质心处径向振动位移矢量。

滑动轴承对该转子系统的径向力F_B和切向力F_T可表示为^[5]：

式中：K_B为轴承径向支承刚度；C为滑动轴承的阻尼系数；复数符号j表示切向力F_T与转子径向振动位移矢量r正交；jCλΩ为轴承的切向刚度。

图1 滑动轴承转子系统模型
Fig.1 Model of sliding bearing rotor system

弹性轴段产生的径向力F_S可表示为：

式中K_S为轴段在集中质量M质心处的等效径向刚度。

由式(2)及(4)，可得转子系统总的径向力F_r：

因此

转子横向运动的阻尼主要为轴承处的流体粘性阻尼：

不平衡产生的离心力F_u：

式中：mr_u和δ分别为转子系统的不平衡量大小和所在的方位角；ω为转子的非同步进动角速度。

转子运动方程可表示为：

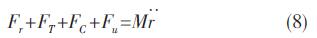
将式(1)~(7)带入式(8)整理后得：

线性微分方程(9)具有如下形式的解：

式中A和α分别表示转子响应的幅度和相位。

将式(10)代入式(9)，简化后得到转子系统的非同步动态响应：

由(11)式得转子系统的非同步动刚度：

式中：K-Mω²为主动刚度；Cω-λΩ为正交动刚度。转子系统失稳本质上是轴系的动刚度减小为零^[5]。此时，应满足下列条件：

将式(13)中的第二式带入第一式可得如下关系：

式中Ω_th即为失稳门槛转速。

式(14)可进一步表示为：

或

式中ω_n为转子系统的无阻尼固有频率。

式(15)给出了滑动轴承转子系统失稳门槛转速与其低阶临界转速之间的关系。

转子失稳大多发生在升速或超速运行过程中。当滑动轴承-转子系统升速到一定转速Ω时，由于滑动轴承油膜而产生的涡动频率(转速)为λΩ，随着转速升高，涡动频率(转速)随之升高，当涡动频率(转速)升高至低阶临界转速ωn 时，产生共振，转子振动幅值会剧烈增大，当外阻尼较小时，系统可能发生次同步失稳。次同步失稳发生后，转子振动将被“锁频”，始终保持等于转子的低阶固有频率ωn，不再随转速的升高而变化。

ωn一般为转子系统的一阶弯曲临界转速(固有频率)，实际中由于系统非线性的影响，发生次同步失稳后，转子振动频谱中除可明显观察到一阶弯曲临界转速对应的突频外，某些情况下，二阶甚至三阶弯曲临界转速对应的突频也有所反映。

在使用滑动轴承的转子系统中，为了保证转子系统的稳定性，必须提高转子系统的失稳门槛转速Ωth至最高工作转速以上。由式(14)和(15)，可采取两种方法来提高失稳门槛转速：

1)提高转子系统的横向弯曲刚度 (提高转子的弯曲临界转速)

提高转子系统的横向弯曲刚度一般通过改变转子的结构尺寸(增大径向尺寸、减小轴向尺寸等方法)来实现。

2)减小轴承内环形流体的周向流速(减小系数 )

减小轴承内环形流体的周向流速一般需采用不同的轴承或密封结构，需对轴承或密封结构进行重新设计修改。不同结构形式的轴承对应的系数λ列于表1中，仅从稳定性角度看，流体静压轴承最好、椭圆瓦和可倾瓦轴承次之，平面圆柱轴承的稳定性最差。系数λ与轴承结构形式、转静件表面的粗糙度、油液粘度、油液温度、轴承预载等多种因素有关，其精确值一般需通过试验获得。

表1 不同结构形式的轴承对应的λ系数
Tab.1 λ coefficients corresponding to different bearing configurations

在保持轴承结构不变的情况下，采取反旋流措施也可减小流体的周向流速，即在轴承或密封环形流体中导入一股与原始流体旋转方向相反的流体以抵消腔内的流动形态。反旋流方法对改善轴系稳定性有一定效果，但结构复杂、设计制造难度大^[6]，实际应用并不多见。

1) 滑动轴承交叉油膜刚度引起的转子次同步失稳存在一失稳门槛转速，该失稳门槛转速与转子的低阶临界转速及轴承结构形式有关，失稳时转子的径向振动突频主要表现为低阶(一般为一阶)弯曲临界转速对应的频率。

2) 可通过提高转子系统低阶临界转速或改变轴承结构形式来提高失稳门槛转速，以确保工作转速下和超速过程中转子工作的稳定性。

3) 在不改变轴承结构形式的前提下，通过修改转子结构，提高其低阶弯曲临界转速，有效地消除了次同步导致的转子失稳。

4) 对于本文的5叶可倾瓦滑动轴承转子系统，转子工作转速Ω与轴颈中心涡动速度(转速)ω满足关系：Ω=0.175ω。根据运转试验获得的临界转速，预测得到新试验转子系统的失稳门槛转速为74 286 rpm，通过动平衡实现了该转子至 50 000 rpm的高速稳定运行。