作者简介:周建(1987—),男,博士,研究领域为虚拟振动技术及气动弹性力学
(Xi’an Aerospace Propulsion Institute, Xi’an 710100, China)
备注
作者简介:周建(1987—),男,博士,研究领域为虚拟振动技术及气动弹性力学
对电动振动台机电耦合系统进行辨识,通过Amesim软件建立了电动振动台的机电耦合模型,在Virtual.lab软件中建立了振动台与试验件的刚柔耦合模型,借助Matlab/Simulink软件建立了振动台的控制系统,最终基于联合仿真技术建立起了闭环虚拟振动台的正弦扫描振动试验平台。通过算例研究,表明所建立的虚拟振动试验平台能够很好地实现对试验件的正弦扫描振动试验,并能够实现仿真结果在Virtual.lab中的可视化。
In this paper, the electromechanical coupling system was identified and then was built in the Amesim environment. The rigid-flexible coupled model of shaker and test specimen was built in the Virtual.lab environment. The control system was modeled by means of Matlab/Simulink. The closed virtual vibration testing platform for sine-sweep test was constructed by using co-simulation technology. The results obtained by simulation example demonstrate the sine-sweep test can be simulated well by using the proposed virtual vibration testing platform and the time dependent stress contour of test part can be displayed in the Virtual.lab.
引言
振动环境试验是很多产品研制过程中的重要环节,对于验证产品的可靠性有着至关重要的作用。而基于振动台的振动环境试验存在周期长、成本高、过试验或欠试验等问题。随着仿真技术的发展,近些年来发展了虚拟振动环境试验技术,从而弥补了真实振动试验的不足,降低试验风险,节省了试验成本。
在国外,虚拟振动试验技术已经应用到了实际工程中[1-3],国内的振动试验仿真技术研究首先由邱吉宝、胡绍全等人于2002年提出[4]。此后,向树红等利用子结构建模方法建立了40吨振动台的有限元模型,基于有限元方法进行了振动试验的虚拟仿真[5-6];范宣华对电振动台的动圈、夹具、试件进行有限元建模并进行了虚拟的随机振动试验仿真[7];张逸波、齐晓军、张丽新等建立了200 kN振动台的动圈有限元模型并进行了控制点控制效果的仿真分析[8];以上的研究主要是将电动振动台的动圈建立了有限元模型,考虑到了动圈的结构动力学特性,但无法考虑整个振动系统的机电耦合效应的影响,且是开环虚拟振动试验。2010年,谭永华、蔡国飙利用振动台的刚体模型、夹具的柔性体模型,通过Virtual.Lab Motion与Matlab/Simulink的联合仿真,进行了夹具的虚拟正弦扫描试验,尽管实现了虚拟振动的闭环仿真,但仍没考虑整个系统的机电耦合效应[9]。张琳等及刘源等在考虑机电耦合效应的影响情况下尝试了闭环虚拟振动试验的实现,但扫描频率范围小,控制效果仍然不是很理想[10-11]。周成等建立了多维虚拟振动试验系统,但没给出相应的建立过程[12]。
本研究采用系统仿真软件Virtual.Lab,Amesim和Matlab/Simulink通过联合仿真技术建立了电动振动台系统的虚拟正弦振动试验平台,并通过算例研究表明此系统可以进行虚拟正弦扫描试验,为后续的虚拟振动试验平台建设工作打下基础。
1 虚拟试验平台建设思路
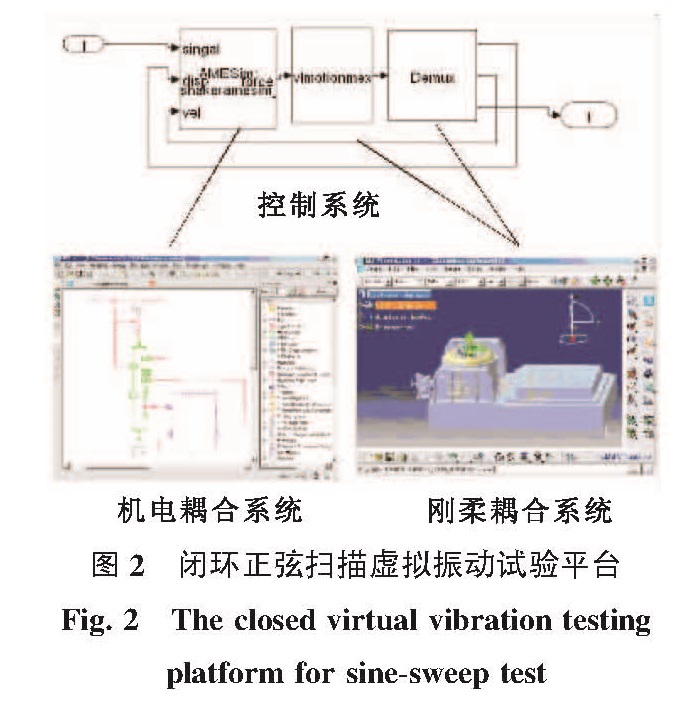
基于联合仿真技术的虚拟振动试验平台建设的基本思路:首先辨识出电动振动台的机电耦合参数模型,通过Amesim建立振动系统的机电耦合模型,然后,用Virtual.Lab Motion建立台体及试验件的刚柔耦合模型,最终将Virtual.Lab Motion和Amesim中的模型编译为Matlab/Simulink可识别的S-function函数,在Matlab/Simulink中实现闭环虚拟振动试验仿真,仿真结果可以同时在Virtual.Lab Motion中显示。
1.1 电动振动台辨识根据电动振动台系统组成与工作原理,可以采用集中参数的拉格朗日方程,将振动台结构的自由度降到有限值,进行足够精度的近似分析。动圈部分的一阶频率决定了振动台的工作频率上限,可将动圈沿轴向方向简化为1个二自由度系统,按其结构特点和功能分为等效台面部分和等效线圈部分,它们之间通过弹簧和阻尼连接;将振动台台体看作刚体,与地面之间通过隔振气囊连接,也可以简化为单自由度弹簧质量系统。这样,振动台的机械部分便缩减为三自由度集中参数模型。三自由度系统的三阶模态决定了振动台系统的动态响应。一阶隔振模态是由隔振装置产生的,由于隔振气囊的刚度很小,一阶频率要小于振动台的工作频率下限,运动形式表现为振动台整体的上下运动;二阶支撑模态是由弹性支撑装置产生的,一般在几十赫兹左右,此时动圈作为一个整体相对于台体上下运动;三阶模态是动圈沿轴向的一阶谐振频率,决定了振动台工作频率的上限,表现为动圈的台面部分和线圈部分之间的相对运动,会对振动台的正常工作产生一定影响。
振动台运动过程中所受的力是由线圈中的交变电流决定的,而电流的大小又受线圈运动速度的影响,这也就是电动振动台的机电效应,如果不考虑线圈电阻和电感随频率和温度变化的影响,施加到振动台线圈的交变电压信号主要由3部分组成,一部分为电流通过线圈电阻产生的电压,另外一部分为线圈电感产生的磁感应电动势,还有一部分为线圈在磁场内运动产生的反电动势。
根据以上的分析,在不考虑台体运动对系统特性的影响,可以得到电动振动台机电耦合系统的数学模型为:

式中:mt为台面质量;mc为线圈质量;kc为线圈和台面之间的刚度;ks为台面支撑气囊的刚度;xt和xc分别为台面和线圈的位移;R和L分别为动圈的等效电阻和电感;u和i分别为输入的电压和线圈中的等效电流;Kf为力常数。
对式(1)进行Laplace数学变换,且考虑到机械元件的阻尼系数,则恒压、恒流驱动下的传递函数可表示为:

式中:ω0=Rks/K2f为系统一阶惯性圆频率;
 为弹性支撑圆频率;
为弹性支撑圆频率; 为电谐振圆频率;
为电谐振圆频率; 为动圈轴向谐振圆频率;ξ1为台面弹性支撑阻尼比;
为动圈轴向谐振圆频率;ξ1为台面弹性支撑阻尼比; 为电阻尼比;ξ3为线圈与台面之间的阻尼比。
为电阻尼比;ξ3为线圈与台面之间的阻尼比。在垂直方向振动台空台和带负载情况下获得恒压、恒流驱动下的振动系统传递函数,根据传递函数可获得式(2)中的参数,这里给出我们经常使用的T 2 000振动台已经辨识出的参数,如表1所示。
1.2 正弦控制算法正弦振动控制主要是实现对响应信号幅值的控制,进行正弦振动控制仿真时,可采用如下方式提取响应信号的幅值:
考虑正弦信号yt=Asin(2πft+φ),其可以描述为如下形式:
y(t)=acos(2πft)+bsin(2πft) (3)
对于一系列的采样点,可得到如下的方程:
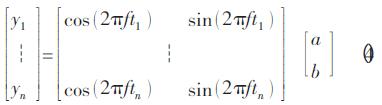
式中:t1表示第1个采样时刻;tn表示第n个采样时刻。根据上式,利用最小二乘法即可获得a 与b的最优估计。正弦信号的幅值即可通过下式计算得出:

对于正弦信号,每一个给定的频率ωi,系统在此频率下的传递函数可以写为:

式中:Ad为响应信号的幅值;Ac为驱动信号的幅值。
对于每一个频率点记参考信号谱在当前频率下的幅值为Aref(ωi),根据当前频率点响应信号的幅值与试验参考幅值采用如下的算法确定下一个频率点系统的反传递函数。

式中:
 ;T(ωi)为系统的反传递函数;c为压缩因子。
;T(ωi)为系统的反传递函数;c为压缩因子。则,下一个频率点的驱动信号幅值为:
 1.3 正弦扫描闭环虚拟振动试验平台建设
1.3 正弦扫描闭环虚拟振动试验平台建设正弦扫描闭环虚拟试验平台建设的思路为:以Matlab/Simulink作为主计算平台,Amesim与Virtual.Lab中的模型都编译为Matlab/Simulink可识别的S-function。在Matlab/Simulink发送电压驱动信号到Amesim中,通过机电耦合系统将电压信号转化为力信号加载到台面(Virtual.Lab中)上,台面受到载荷作用后会产生位移、速度和加速度信号,台面的位移、速度信号又会传送给Amesim,对动圈产生力的作用,而台面的加速度信号经过幅值提取,将幅值信号发送到Matlab/Simulink中,在Matlab/Simulink中通过幅值控制算法对其电压信号进行调整,这就形成了一个闭环虚拟试验平台系统,具体的原理图如图1所示。
通过软件之间的联合仿真技术实现正弦扫描闭环虚拟振动试验平台的实现方式如图2所示。
2 算例研究
这里给出一个算例来说明基于联合仿真技术的闭环正弦扫描虚拟振动试验平台的实用性,试验件的有限元模型如图3所示。在底部固支的情况下,此试验件的前两阶固有模态如图4所示,第一阶为上下弯曲模态,模态频率为111.26 Hz,第二阶为左右弯曲模态,模态频率为297.93 Hz。用虚拟振动平台对此试验件进行正弦振动扫描试验,正弦振动扫描的频率为2~200 Hz,在这个频段内,通过振动试验可以扫描出试验件的第一阶固有频率。
图5示出了正弦振动扫描试验的控制谱,通过与参考谱的比较,可以发现在低频阶段控制有些波动,这与压缩因子的选取有关,随着扫描频率的增加,其控制效果也越来越好,在扫描到110 Hz左右时出现波动,说明此处接近于试验件的共振点,这在实际的试验中也会出现共振点附近控制谱波动的现象。通过对试验件端部节点响应进行频谱分析,得到其幅频特性曲线,如图6所示,发现其共振频率为112 Hz,与有限元分析结果基本一致,相差仅0.67%,说明本文建立的虚拟振动试验平台是可以用于正弦振动扫描试验。此外,可以在Virtual.lab中显示出试验件的应力随扫描过程的变化云图及某一响应点的时域响应曲线,如图7所示。
3 结论
对振动台的多学科集成仿真技术进行了研究,在不同软件中建立了振动台控制系统、机电耦合系统和刚柔耦合系统,通过联合仿真技术建立了闭环正弦扫描虚拟振动试验平台。通过算例研究,正弦扫描试验得到的模态频率与有限元计算的模态频率相差仅0.67%,表明了此虚拟振动试验平台可用于正弦扫描试验。此外,实现了试验件应力虚拟振动试验过程中的可视化。
- [1]RICCI S, PEETERS B, DEBILLE J, et al. Virtual shaker testing; A novel approach for improving vibration test performance[C]. International Conference on Noise and Vibration Engineering. Leuven: Katholieke University Leuven, 2008: 1767-1782.
- [2]RICCI S, PEETERS B. Virtual shaker testing for predicting and improving vibration test performance[C]. Proceedings of the IMAC-XXVⅡ, Orlando, 2009:1-16.
- [3]BETTS J, VANSANT K, PAULSON C, etc. Smart testing using virtual vibration testing[C]. In Proceedings of the 24th Aerospace Testing Seminar(ATS), Manhattan Beach, 2008: 103-111.
- [4]邱吉宝, 胡绍全. 结构振动台试验仿真技术研究总结报告[R]. 北京: 总体工程研究所, 2002.
- [5]向树红, 晏廷飞, 邱吉宝. 400 kN振动台虚拟试验仿真技术研究[J]. 航天器环境工程, 2003, 20(4): 25-33.
- [6]向树红, 晏廷飞, 邱吉宝, 等. 40吨振动台虚拟试验仿真技术研究[J]. 宇航学报, 2004, 25(4): 375-381.
- [7]范宣华, 胡绍全, 王东升, 等. 电动振动台随机振动试验有限元仿真[J]. 2008, 4(2): 41-43.
- [8]张逸波, 齐晓军, 张丽新. 200 kN振动台动圈建模与仿真分析[J]. 航天器环境工程, 2009, 26(3): 244-247.
- [9]谭永华, 蔡国飙. 振动台虚拟试验仿真技术研究[J]. 机械强度, 2010, 32(1): 30-34.
- [10]张琳, 邓长华, 谭永华, 等. 随机振动试验仿真技术研究[J]. 机械强度, 2011, 33(6): 927-931.
- [11]刘源, 董立珉, 孔宪仁, 等. 飞行器虚拟振动试验平台构建[J]. 光学 精密工程, 2013, 21(5): 1258-1264.
- [12]周成, 李家文, 李永, 等. 多维虚拟振动试验系统设计及应用[J]. 火箭推进, 2013, 39(4): 85-91. ZHOU C, LI J W, LI Y, et al. Design and application of multi-dimensional virtual vibration testing system[J]. Journal of rocket propulsion, 2013, 39(4): 85-91.