作者简介:陈军军(1985—),男,硕士,研究领域为航天压力容器设计
(1. 上海空间推进研究所,上海 201112;2. 上海空间发动机工程技术研究中心,上海 201112)
(1. Shanghai Institute of Space Propulsion, Shanghai 201112, China;2. Shanghai Engineering Research Center of Space Engine, Shanghai 201112, China)
备注
作者简介:陈军军(1985—),男,硕士,研究领域为航天压力容器设计
针对空间压力容器常规设计方法难以满足航天技术快速发展对轻质量、低成本、高可靠的需求,基于可靠性理论中应力-强度干涉模型,建立空间压力容器可靠性设计数学模型。结合某型号钛合金球形气瓶随机变量统计数据,开展了气瓶可靠性定量设计。计算结果表明,可靠性定量设计方法能够给出产品可靠度定量指标,并在一定程度上降低空间压力容器结构重量。
With the rapid development of aerospace technology, the conventional design method of the space pressure vessel can hardly meet the requirements of light weight, low cost and high reliability. The mathematic model for reliability design of the space pressure vessel is established based on the stress-strength interference model. The quantitative design for gas cylinder reliability is conducted in combination with the random variable statistical data of globular gas bottle made up of titanium alloy. The computation result indicates that the reliability design method can provide quantitative indexes for degree of reliability, and to some degree, can also reduce the weight of the space pressure vessel.
引言
随着航天技术的快速发展,航天器对推进剂贮箱、气瓶等空间压力容器的要求越来越高,如轻质化、低成本、高可靠等,且需在高温、深冷、高真空、强振动、强腐蚀等苛刻条件下工作。因此,设计轻质量、低成本、高可靠,且能够适应复杂空间环境的压力容器是未来的发展趋势。
目前,空间压力容器的设计主要采用确定性设计方法(常规设计及分析设计),即假设各设计变量为确定值,依据给定的安全系数进行设计。确定性设计方法简单、直观,但计算结果偏向保守,逐渐难以适应航天器对组件轻质化、低成本等要求,并且确定性设计方法无法定量给出产品可靠性指标。
针对空间压力容器现有的研制瓶颈,采用一种新的设计方法——压力容器可靠性设计方法[3]。在压力容器设计过程中,充分考虑影响压力容器强度、应力的随机因素,运用概率统计方法确定随机变量参数及分布模型,并参与设计计算,根据系统分配的可靠性指标给出最佳的设计参数。
1 应力-强度干涉理论
可靠性设计方法是以应力-强度干涉模型和功能时效极限状体函数理论为基础,将与设计有关的载荷、强度、寿命等都视为服从一定分布的随机变量,通过数据统计确定其分布规律,并利用概率方法计算出给定设计条件下产品的失效概率和可靠度,以保证所设计的机械产品符合给定可靠性指标要求。
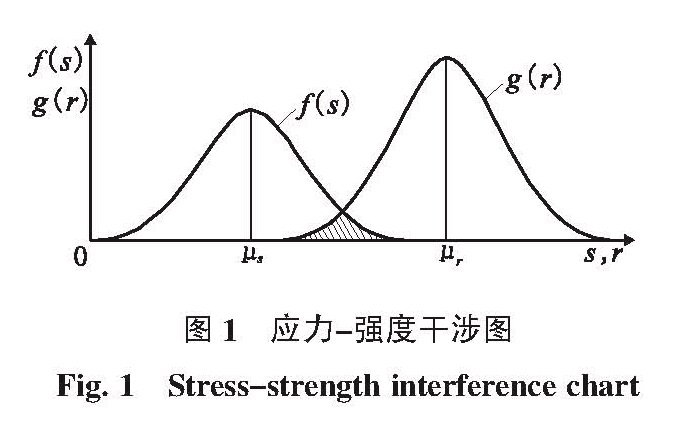
可靠性设计中认为所设计的产品总存在着一定的失效可能。施加于产品上的物理量中,如载荷、工作温度、介质物性等,所有可能引起设计产品失效的因素,一概称之为应力,用s表示;所有阻碍设计产品失效的因素,即产品能够承受这种应力的程度称为强度或抗力,用r表示。产品的可靠度也可以看成产品在给定的运行条件下对抗失效的能力,即应力与强度相互作用(干涉)的结果。如果应力作用效果大于强度,则设计对象失效;反之,设计对象是可靠的。
如果将应力与强度都看成是随机变量,它们的分布密度分别记为f(s)与g(r)。一般情况下s,r与f(s),g(r)之间常为图1所示的“干涉”状态,而所需求的可靠度,就是设计对象的应力与强度相互“干涉”时,设计对象的强度大于应力的概率,即
R=P(r>s)=P(r-s>0) (1)
从图1所示可见,“干涉”的面积越小,可靠性越高。
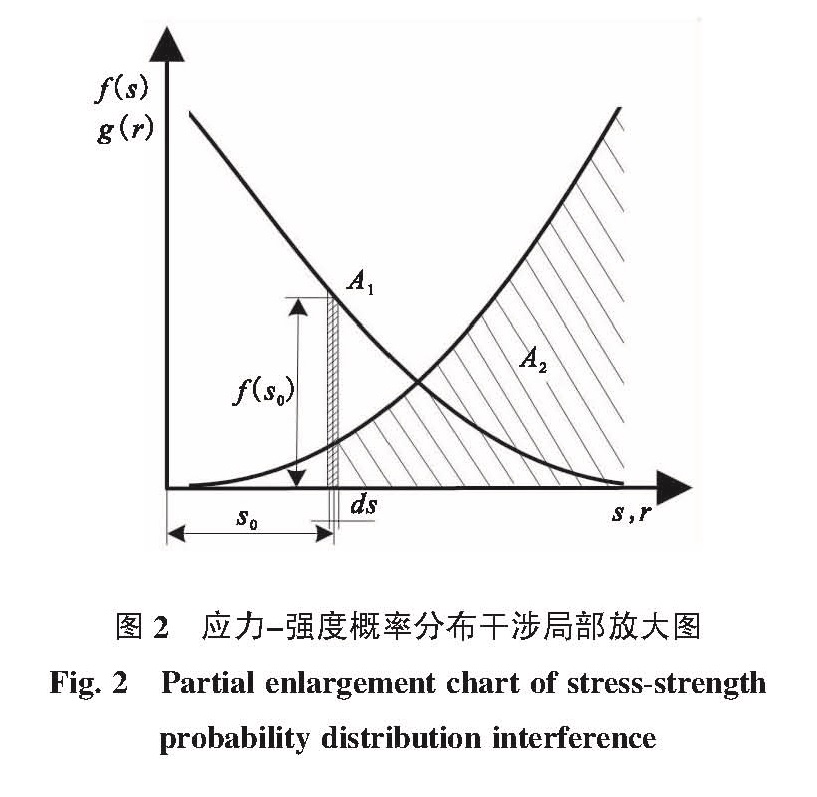
图2是图1所示应力-强度概率分布曲线发生干涉时的局部放大图形,求可靠度就是求强度大于应力情况的发生概率Pr>s。
图2 应力-强度概率分布干涉局部放大图
Fig.2 Partial enlargement chart of stress-strength probability distribution interference首先在干涉区取以应力值s0为中心的微单元ds,则应力出现在ds区间的概率为:

式中A1为图示矩形面积。
再看强度值大于应力值s0的概率为
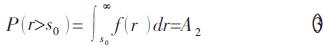
式中A2为图示强度概率分布曲线fr在s0坐标点以右与水平坐标轴围成的面积。
式(2)和式(3)表示的是两个独立事件各自发生的概率,如果这两个事件同时发生,则可应用概率乘法定理来计算应力值为s0时的不失效概率,即可靠度,得
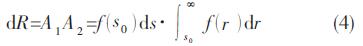
因为产品的可靠度包括所有可能的应力值si 均小于强度值的整个概率,所以需再对上式进行积分,有
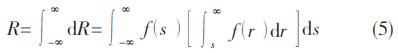
对于某一具体问题,如已知应力取值的最小和最大值分别为a和b,强度的最大取值为c时,则可把式(5)中的边界替代为

式(5)和式(6)则为可靠度计算的一般表达式。
2 空间压力容器可靠性设计模型
空间压力容器的应力和强度是由载荷、尺寸、材料属性等多种因素影响的,通过对这些影响因素的历史数据进行统计分析,均服从正态分布。根据正态分布函数的特性可知,空间压力容器的应力和强度也服从正态分布,其分布密度函数分别为[4]:
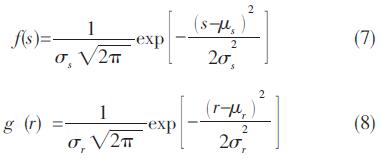
式中:μs和μr为空间压力容器的应力与强度的均值;σs和σr为空间压力容器的应力与强度的标准差。
已知可靠度是强度大于应力的概率,即
R=P[(r-s)>0 ] (9)
现引入新变量y,令
y=r-s (10)
工程上称式(10)为极限状态函数或强度差。由于r和s均为服从正态分布的随机变量,故y也是服从正态分布的随机变量,其分布密度为
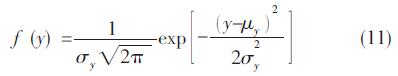
于是可靠度可写成

将式(12)标准化,令

则

因此

当y=0时,z的积分下限应为

由分布函数的代数运算可得

工程上称式(17)为耦合方程(或联结方程)。
把联结方程(17)的负值定义为可靠性的安全指标β,即
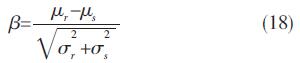
这样就得到了应力-强度干涉模型中应力和强度均为正态分布时可靠度的基本算法。
于是式(15)可写成
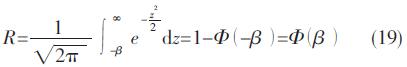
不难看出,β与R之间存在着一一对应的关系。β大时,R大;β小时,R就小;即β的大小反映了压力容器的安全度,因而将其定为安全指标。β与R之间对应关系可通过查标准正态分布积分表得到。
3 钛合金球形气瓶可靠性定量设计
4 结论
通过对强度-应力干涉模型分析研究,建立空间压力容器可靠性定量设计模型,结合随机变量数据统计分析,对某型号用20L钛合金球形气瓶进行设计计算。通过计算结果分析可以得出以下结论:
1)可靠性设计方法能够给出产品定量可靠性指标;
2)采用可靠性设计方法,在满足定量可靠性指标要求的前提下,可降低空间压力容器结构重量;
3)可靠性设计关系到随机变量分布函数的确定,需要通过大量试验、检测等数据的积累和统计,确定随机变量分布函数类型及其数字特征。
钛合金气瓶具有结构简单、空间环境适应性强、疲劳寿命高等特点,为典型的空间压力容器产品,在国内外广泛地应用于载人、长时间在轨、低轨道环境的飞行器中。本文以20 L钛合金球形气瓶为研究对象,研究空间压力容器可靠性设计方法及其计算过程。
20L钛合金球形气瓶设计压力p为23+10 MPa,材料为TC4钛合金(时效处理后要求值:σb1 078 MPa,σs≥1 029 MPa),安全系数2倍,可靠度要求为0.999 9,试计算气瓶壁厚。
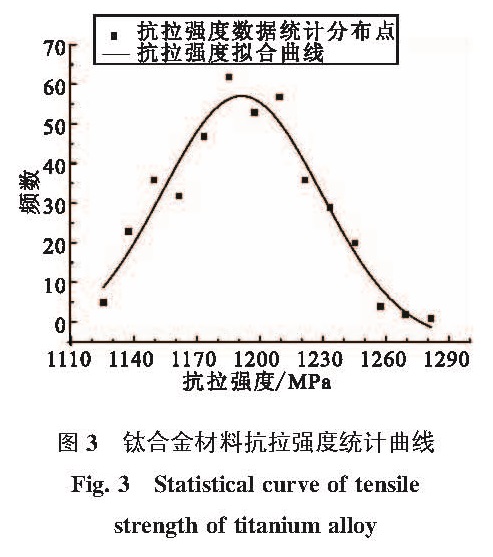
3.1 材料数据统计分析材料的力学特性直接决定了产品的强度特性,受到材料的冶炼工艺、加工工艺及热处理工艺等因素影响,其各项力学特性参数呈现随机变化。根据材料的力学试验数据,统计分析得到材料力学性能的分布曲线,见图3。
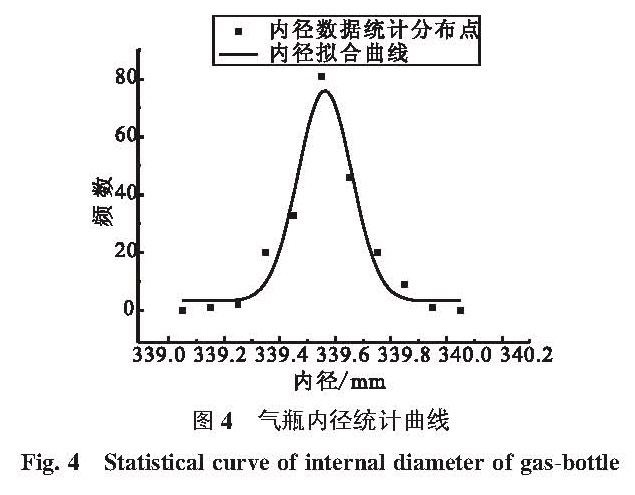
3.2 设计尺寸数据统计分析几何尺寸是决定压力容器应力的重要因素,由于加工制造工艺的精度、量具的精度、操作人员的技术水平等影响,使得同一批产品可能在加工完成后会存在尺寸的差异,这种差异存在的范围就是压力容器尺寸作为一个随机变量的分布范围。根据现有的加工技术水平,测试相关产品数据,统计分析得到几何尺寸变量的分布曲线,见图4和图5。
3.3 载荷数据统计分析在常规压力容器设计中,通常把载荷值视为一个确定的常量,但事实上,压力容器所受载荷的大小都是在一定范围内分布,是一个随机变量。气瓶所受载荷为内压,通过大量试验数据统计表明,内压的分布形式为正态分布。根据正态分布的性质可知,当服从正态分布的随机变量取值为μ±3σ滓时,就基本上包含了该随机变量的全部概率,即“3σ”法则。于是可以把设计压力视为均值,而把极限偏差看成是3σ滓,即:
μp=n×P=2×23=46 MPa
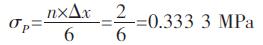
式中:n为安全系数;Δx为极限偏差。
3.4 应力均值及标准差确定球形气瓶在承受内压载荷情况下,轴向及周向应力相等,由球壳应力计算公式(注:为了简化运算,用内径Di代替中径D):

得气瓶应力均值为
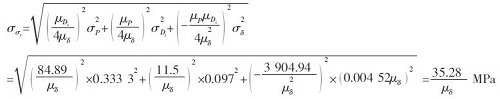
根据分布函数的代数运算法则,求应力标准差:
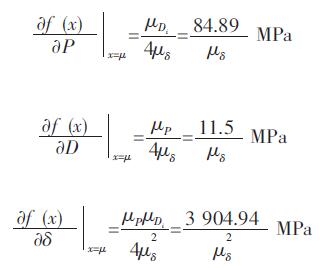 3.5 压力容器壁厚计算3.5.1 可靠性定量设计计算
3.5 压力容器壁厚计算3.5.1 可靠性定量设计计算气瓶的可靠度要求为0.999 9,经查标准正态分布积分表,得安全指标β为3.719,将强度、应力均值及标准差带入联结方程(18)得:
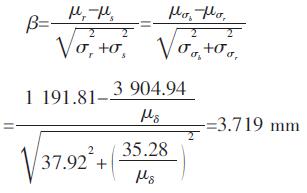
解得
μδ=3.3 mm;σδ=Cδ×μδ=3.3×0.004 52=0.014 9 mm;即气瓶的设计壁厚为3.3 mm,公差为±0.05 mm。
3.5.2 常规设计计算已知气瓶设计压力23 MPa,根据容积计算得到气瓶内径为340 mm,气瓶材料为TC4钛合金,其性能为σb=1 078 MPa,σs=1 029 MPa,根据QJ1654《钛合金球形气瓶设计准则》中许用应力确定方法,许用应力为
 。根据球壳壁厚计算公式
。根据球壳壁厚计算公式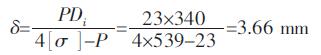
通过两种设计计算方法对比可知,可靠性设计计算得气瓶的壁厚为3.3 mm,气瓶壁厚减薄约8.2%。同时,可靠性设计定量地反映了气瓶的可靠程度或者说气瓶的失效概率(可靠度0.999 9)。
- [1]姚新宽, 战侦文, 朱加琦. 压力容器应力分析设计方法的进展和评述[J]. 石化技术, 2016 (1): 137.
- [2]申余华. 压力容器设计方法探讨[J]. 科技展望, 2015 (8): 130.
- [3]WANG L B, QIN Z Z. Analysis of reliability for aerospace pressure vessel design & analysis [M]//Design & analysis. [S.l.]: [s.n.],1989.
- [4]李亚萍, 冯淑红, 柳征勇. 应力-强度模型的干涉区与可靠度研究[J]. 上海航天, 2014, 31(6): 133-135.
- [5]马世骏. 关于应力-强度干涉模型的干涉面积的分析[J].西南交通大学学报, 1984 (3): 35-42.
- [6]郝静如. 机械可靠性工程[M]. 北京: 国防工业出版社,2011.
- [7]孙志国. 化工压力容器可靠性设计[J]. 盐城工学院学报,1996, 9(4): 48-50.
- [8]季维英. 压力容器的可靠性设计[J]. 南通职业大学学报,2005, 19(4): 69-71.
- [9]叶乾惠, 秦晓钟, 汪子云,等. GB150-2011钢制压力容器[S]. 北京: 中国标准出版社, 2011.