收稿日期:2017-09-30
作者简介: 姜凯(1993—),男,硕士,研究领域为氢氧火箭发动机燃烧过程数值仿真
作者简介: 姜凯(1993—),男,硕士,研究领域为氢氧火箭发动机燃烧过程数值仿真
Computation and analysis of thermodynamic parameters of shock wave and detonation wave in H2/O2 rocket engine
JIANG Kai,HE Yunqin, LIANG Guozhu
(School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100083, China)
hydrogen-oxygen rocket engine; shock wave; detonation wave; thermodynamic parameter; pressure ratio
备注
摘要
全文
图/表
参考文献
大扩张比氢氧发动机在地面试车时喷管中可能会出现激波,而在起动时刻燃烧室或燃气发生器中则很容易产生爆轰波,其对发动机的结构与工作状态会产生较大的影响。为准确地分析激波与爆轰波对氢氧发动机的影响,从热力参数层面进行计算分析,所有的计算都考虑热化学反应的影响。首先,在传统一维管流模型基础上引入化学平衡模型来计算和分析推进剂混合比和燃烧室压力对喷管扩张段中激波位置及热力参数影响的一般规律; 然后,采用基于热化学平衡模型的C-J爆轰理论,计算和分析推进剂混合比、初温及初压对爆轰波的影响规律。计算分析表明:喷管扩张段中的激波位置与燃烧室压力呈线性关系,激波处的温度比相对于不考虑热化学反应时要低28%～38%,而压力比无明显区别,压力比与温度比在化学当量混合比时最小; 爆轰波强度随着初压的升高、初温的降低而增强,在化学当量混合比时最强,初温30 K,初压1 MPa时爆轰压力最高可达220 MPa,温度可达4 500 K,波速超过3 000 m/s。得到的这两种波的规律和特点可以为发动机工程设计人员提供一定的参考。
In order to analyze the effects of shock wave and detonation wave on hydrogen oxygen engine more accurately, the thermodynamic parameters are calculated and analyzed, in which the influence of thermo-chemical reactions are fully considered. Dased on the traditional one-dimensional pipe flow model, a chemical equilibrium model is introduced to calculate and analyze the general law of the influence of propellant mixture ratio and chamber pressure on the shock position and thermal parameters, and then the C-J detonation theory based on thermo-chemical equilibrium is used to calculate and analyze the effects of propellant's mixing ratio, initial temperature and initial pressure on detonation wave. The results show that the shock positions in the nozzle expansion section are linear to the pressure in the combustion chamber, and the temperature ratio at the shock wave is about 28%～38% lower than that without thermo-chemical reaction, where the pressure ratio has no significant difference. The temperature ratio and the pressure ratio are minimum at the stoichiometric mixture ratio. The results also show that the detonation wave intensity enhances with the increase of initial pressure and the decrease of initial temperature. And it becomes strongest at the stoichiometric mixture ratio. The detonation pressure and temperature can be up to 220 MPa and 4 500 K respectively, and the wave velocity exceeds 3000 m/s when the initial temperature is 30 K and the initial pressure is 1 MPa. The rules and characteristics of these two kinds of waves in rocket engines can provide a certain conference for engine engineers.
引言
激波是气体在超声速运动过程中最重要的现象之一。通过分析国内外多种不同型号的氢氧发动机的工作压力和喷管扩张比来看,由于大扩张比的影响,多款发动机在地面及低空工作环境中其喷管扩张段可能出现激波。激波的出现会导致压强与温度等热力参数的突变,掌握其规律和特点对工程中发动机的设计具有一定的实际意义。
国内外对激波进行了大量研究[1-5],目前相关理论和数值方法都已比较成熟。本文将在传统一维管流模型基础上引入化学平衡模型(即平衡流动模型)来分析氢氧发动机喷管扩张段中的激波,以便获得较为细致准确的计算结果,并系统地计算和分析推进剂混合比和燃烧室压力对激波的位置及激波处热力参数的影响规律。
爆轰波是氢氧发动机在起动时刻容易产生的另外一种形式的激波,与普通意义上的激波的本质区别是:爆轰波是一种激波和燃烧波的紧密耦合形式,而非单纯的强压缩波。爆轰常常导致极强的冲击波,一般在氢氧发动机的点火起动时在发动机燃烧室和燃气发生器中可能会发生,由于其产生的瞬时压力极大,常常具有较大的破坏作用。如欧洲阿里安火箭几次发射失败都与第三级发动机HM-7的故障有关,其燃气发生器在点火过程中会出现极大的压力峰[6-7]。我国某氢氧发动机的燃气发生器在点火起动时也有类似的现象。故分析氢氧发动机在不同点火条件下的爆轰规律对发动机的设计以及氢氧推进剂的进入时序控制具有一定的指导作用。
关于爆轰波的理论和实验研究早在上个世纪40年代就开始了,从经典的C-J爆轰理论[8-9]到层流爆轰波面结构模型(ZND模型)[10-12],再到单螺旋、两头和多头模式结构等各种物理模型[13-14],爆轰波模型逐渐丰富完善。国内各研究院所和大学也对爆轰的理论和应用开展了诸多研究[15-19],对爆轰理论及爆轰特性进行了系统地研究与总结,并获得了诸多成果。此外,爆轰的仿真结果也表明低温条件下的爆轰强度很大,对发动机工作性能有很大影响[20-22]。
已有研究结果表明,一方面关于爆轰的理论发展了近80年,但由于爆轰波的传播速度极快,使用现有实验设备仍难以对其进行充分地观测,对于爆轰波的三维结构细节和物理机制细节,仍不十分清楚; 另一方面从工程实践层面来看,C-J理论可以对爆轰波的宏观参数(如波速、压比等)给出相对可靠的数值预测。因此,本文将采用C-J爆轰理论编写热力参数计算程序,并考虑热化学反应过程,针对航天氢氧发动机的工作状态,来研究混合比、初压与初温等参数对发动机点火过程中可能出现的爆轰波现象的影响规律及相应的爆轰热力参数变化规律。
1 激波热力参数计算分析
2 爆轰波热力参数计算分析
3 结论
通过对氢氧发动机在不同工作状态下可能出现的激波与爆轰波现象进行计算,分析二者影响下的热力参数变化,结论如下:
1)引入热化学反应后激波计算结果表明,压比与经典理论计算结果相近,偏差在1%以内,温度比偏低,最大可达38%;
2)常用氢氧发动机扩张比较大,近地面工作阶段可能产生激波,激波位置与室压线性相关,室压越大,激波位置越靠近喷管出口,混合比越接近化学当量混合比,激波作用下的压比与温度比越低;
3)决定爆轰强度的最主要因素为初温,初温越低,爆轰强度越大,推进剂越接近当量混合比,初压越大,爆轰强度也越大;
4)爆速主要由混合比与初压决定,在可爆轰范围内,氧氢混合比越小,初压越大,爆速越高;
5)低温氢氧发动机点火时若发生爆轰,压强与温度会剧增,如初温为30 K、初压为1 MPa时,瞬间高压可能达到220 MPa,温度可达4 500 K以上,对发动机造成冲击甚至破坏;
6)为了消除爆轰波,应尽量避免氢氧的大量堆积,使其避开氢氧的爆轰极限(如点火时采用合理的推进剂注入时序、点火方式或点火位置等)。
- [1] 泽尔道维奇. 激波和高温流体动力学现象物理学[M]. 张树材, 译. 北京:科学出版社, 1980.
- [2] MURMAN E T. Analysis of embedded shock waves calculated by relaxation methods [J]. AIAA journal, 2015, 12(5): 735-736.
- [3] 申义庆, 高智, 杨国伟. NS方程激波计算的摄动有限差分方法[J]. 空气动力学学报, 2006, 24(3): 335-339.
- [4] FETEANU R, GREATRIX D. Traveling shock wave interaction with rocket motor head end [C]// AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. [S.l.]: AIAA, 2013: 123-129.
- [5] 路媛媛, 张蒙正, 严俊峰. 火箭推力室喷管内激波对RBCC性能影响分析[J]. 火箭推进, 2013, 39(5): 46-50.
- [6] 谢晓亮. 阿里安火箭5次发射失败简况[J]. 中国航天, 1990(6): 25.
- [7] 朱森元. НМ-7氢氧发动机[J]. 导弹与宇航, 1978(3): 88-108.
- [8] CHAPMAN D L, CHAPMAN D L. On the rate of explosion in gases [J]. Philosophical magazine, 2009, 47(284): 90-104.
- [9] JOUGUST E. On the propagation of chemical reaction in gases [J]. J de mathematiques pures et appliquees, 1905(l): 347-425.
- [10] ZELDOVICH Y B. On the theory of the propagation of detonation in gaseous systems [J]. Technical report archive & image library, 1950, 10(1261): 542-568.
- [11] VON NEUMANN J. Theory of detonation wave [M]. New York: Pergamon Press, 1963: 1903-1905.
- [12] DORING W. On the detonation process in gas [J]. Annal phys, 1943(43): 421-436.
- [13] TSUBOI N, ETO K, HAYASHI A K. Detailed structure of spinning detonation in a circular tube [J]. Combustion & flame, 2007, 149(1): 144-161.
- [14] NAGAO T, ASAHARA M, HAYASHI A K, et al. Numerical analysis of spinning detonation dependency on initial pressure using AUSMDV scheme [C]// AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. [S.l.]: [s.n.], 2015: 717-727.
- [15] 严传俊, 范玮, 黄希桥,等. 新概念脉冲爆震发动机的探索性研究[J]. 自然科学进展, 2002, 12(10): 1021-1025.
- [16] YANChuanjun, FAN Wei, HUANG Xiqiao, et al. Exploratory study on new pulse detonation engines [J]. Progress in natural science: materials international, 2003, 13(2): 88-94.
- [17] 张博. 气相爆轰动力学[M].北京: 科学出版社, 2012.
- [18] 郭红杰, 梁国柱, 马彬,等. 爆震波点火器在氢氧塞式喷管的工程应用[J]. 火箭推进, 2006, 32(6): 16-19.
- [19] 郭红杰, 梁国柱. 爆震波点火器管路传播过程数值模拟[J]. 推进技术, 2006, 27(1): 83-87.
- [20] TSUBOI1Nobuyuki, FUJIMOTO Keisuke, MUTO Daiki. Three-dimensional numerical simulation on dispersion process of unsteady high pressure hydrogen jet flow: AIAA 2017-1232 [R]. USA: AIAA, 2017.
- [21] CAI Xiaodong, LIANG Jianhan, DEITERDING Ralf, et al. Adaptive simulations of cavity-based detonation in supersonic hydrogen oxygen mixture [J]. International journal of hydrogen energy, 2016, 41: 6917-6928.
- [22] COYE B, WATTS J M. Cryogenic, multiphase, hydrogen-oxygen detonations: AIAA 2005-1462 [R]. USA: AIAA, 2005.
- [23] GORDON S, MCBRIDE B, ZELEZNIKF J. Computer program for calculation of complex chemical equilibrium compositions and applications. Supplement 1: Transport properties: NASA 85-16663 [R]. USA: NASA, 1985.
- [24] REYNOLDS W C. The element potential method for chemical equilibrium analysis: implementation in the interactive program STANJAN, Version 3 [R]. [S.l.]: [s.n.], 1986.
- [25] 李宜敏,张中钦,张远军. 固体火箭发动机原理[M]. 北京: 北京航空航天大学出版社, 1991.
由于起动时刻的推进剂流量、推进剂进入时序以及雾化蒸发等复杂因素的综合作用,火箭发动机的燃烧室和燃气发生器在点火起动时刻往往容易形成氢氧混合物的瞬时大量堆积,且由于点火时混合物的初始压力一般都较高,故容易产生高强度的爆炸甚至是爆轰。
2.1 爆轰波计算方法与结果验证在计算分析之前,首先需要确定计算方法、编制程序并通过经典算例来验证程序。
2.
1.1 计算方法采用C-J爆轰理论[28]来计算氢氧爆轰参数,该理论认为爆轰波是一种伴随有化学反应热放出的强间断面的传播,以热力学与流体动力学理论为基础,提出并论证了爆轰波稳定传播的条件与表达式。在其基础上引入热化学平衡模型,在求解过程中实时调用热力计算程序,采用与激波相同的平衡态计算方法,对迭代过程中的系数进行修正,以提高计算精度。
爆轰波前后的连续、动量、能量方程与激波一致,再加上C-J条件即爆轰后气流速度等于当地声速(u2=a2)和气体状态方程(pM=ρRT)可以导出:
(p1)/(p2)=1-γS,2((ρ2)/(ρ1)-1)(10)
h2=h1+((RγS,2T2)/(2M2))[((ρ2)/(ρ1))2-1](11)
采用与激波相同的处理方式可以得到相应的Newton-Raphson迭代公式:
((p″-(p1)/(p2)))/(ln((p2)/(p1)))Δln(p2)/(p1)+((p″-(p1)/(p2)))/(ln((T2)/(T1)))Δln(T2)/(T1)=(p1)/(p2)-p″(12)
(((h″-h2)/R))/(ln((p2)/(p1)))Δln(p2)/(p1)+(((h″-h2)/R))/(ln((T2)/(T1)))Δln(T2)/(T1)=(h2-h″)/R(13)
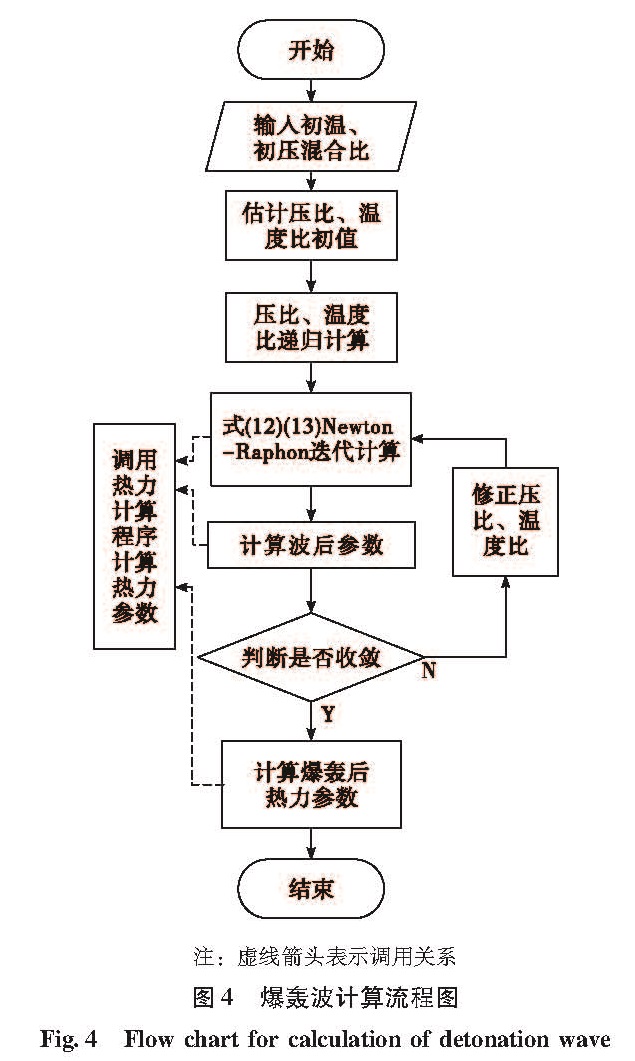
基于上面导出的爆轰波计算公式,参照文献[26],爆轰波的计算共分三步进行:第一步是由方程(14)估计压力与温度的初值; 第二步是由递归公式(式15、16)修正估计值; 第三步是由Newton-Raphson迭代公式得到最终值。详细流程见图4。
图4 爆轰波计算流程图
Fig.4 Flow chart for calculation of detonation wave{p2/p1=15
h2=h1+3/4(RT1)/(M1)((p2)/(p1))0(14)
((p2)/(p1))k+1=(1+γs.2)/(2γs.2αk){1+[1-(4γs.2αk)/((1+γs.2)2)]1/2}(15)
((T2)/(T1))k+1=((T2)/(T1))0-3/4R/(M1(Cp)2)((p2)/(p1))0+
(Rγs.2)/(2M1(Cp)2)((rk+12-1)/(rk+1))((p2)/(p1))k(16)
其中
αk=((T2)/(T1))k((M2)/(M1)),rk+1=αk((p2)/(p1))k+1
式中:p为压力; T为温度; ρ为密度; h为焓值; R为气体常数; γs.2为比热比; M为平均分子质量; 下角标1为爆轰前参数; 下角标2为爆轰后参数。
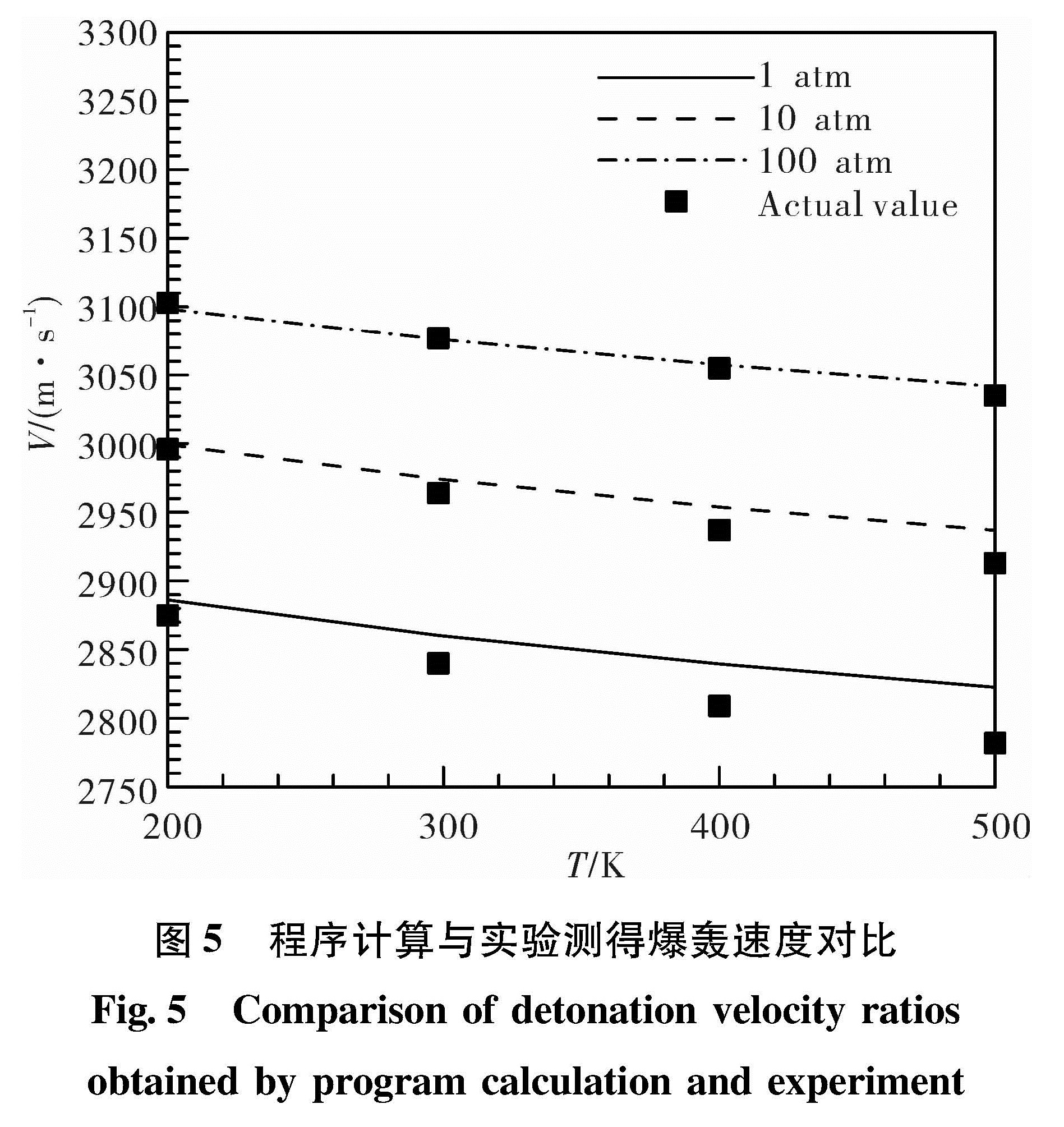
2.1.2 结果验证由于爆轰波结构十分复杂,目前对于其爆轰的原理与具体结构仍不清晰。通过查阅文献可知爆轰速度可以通过实验精准测量得到,并且爆轰的热力参数也可由爆轰速度表征,所以选取爆轰速度进行结果验证。与文献[27]中数据的对比见表3与图5,计算中取混合比为化学当量混合比。对比结果显示,程序计算结果与文献中实际值的误差在1%以内,结果可信度较高,可以认为该计算方法是正确的。
表3 爆轰参数数据对比
Tab.3 Comparison of detonation parameters2.2 计算结果分析根据C-J爆轰理论,影响爆轰强度的核心因素有三个:混合比K、初压p1和初温T1。本节将主要从这三个方面来进行计算和分析。根据氢氧爆轰极限与点火范围,选定计算K为2～64,T1为30～300 K,p1为10-5～20 atm。此外,在火箭启动时刻,液氢/液氧的雾化、蒸发、混合、堆积可能会产生近30 K的氢氧混合物(其中氢为气态,但氧可能处于液态甚至是固态),且由文献[28]中的介绍可知,当液相颗粒小于20 μm时,考虑液相的计算结果与气相的计算结果之间的偏差不大于2%。而在发动机中,氧雾化的颗粒很小,可以迅速的蒸发。故本文在选定的初温范围内统一将其简化为气相爆轰来研究。
图5 程序计算与实验测得爆轰速度对比
Fig.5 Comparison of detonation velocity ratios obtained by program calculation and experiment2.2.1 混合比、初压对爆轰参数的影响规律为了分析混合比、初压对爆轰参数的影响规律,需要设定一个初温,这里选择氢氧发动机点火时的温度,约为100 K。初压p1的范围取为10-5～20 atm、混合比K的范围取为2～64。计算可得压力比、温度比以及爆轰速度的变化曲线(见图6)。由图6(a)与6(b)可知,爆轰作用下,气体前后压比、温度比相对于K的变化规律一致,在接近当量混合比时有最大值。随p1的增大,爆轰前后压力与温度比增大,压力比最大可达65,温度比可达45。由图6(c)所示,爆轰速度随K增大逐渐降低,且p1越大,爆速越高,最高爆速约3 800 m/s。
图6 爆轰参数随混合比和初压的变化曲线
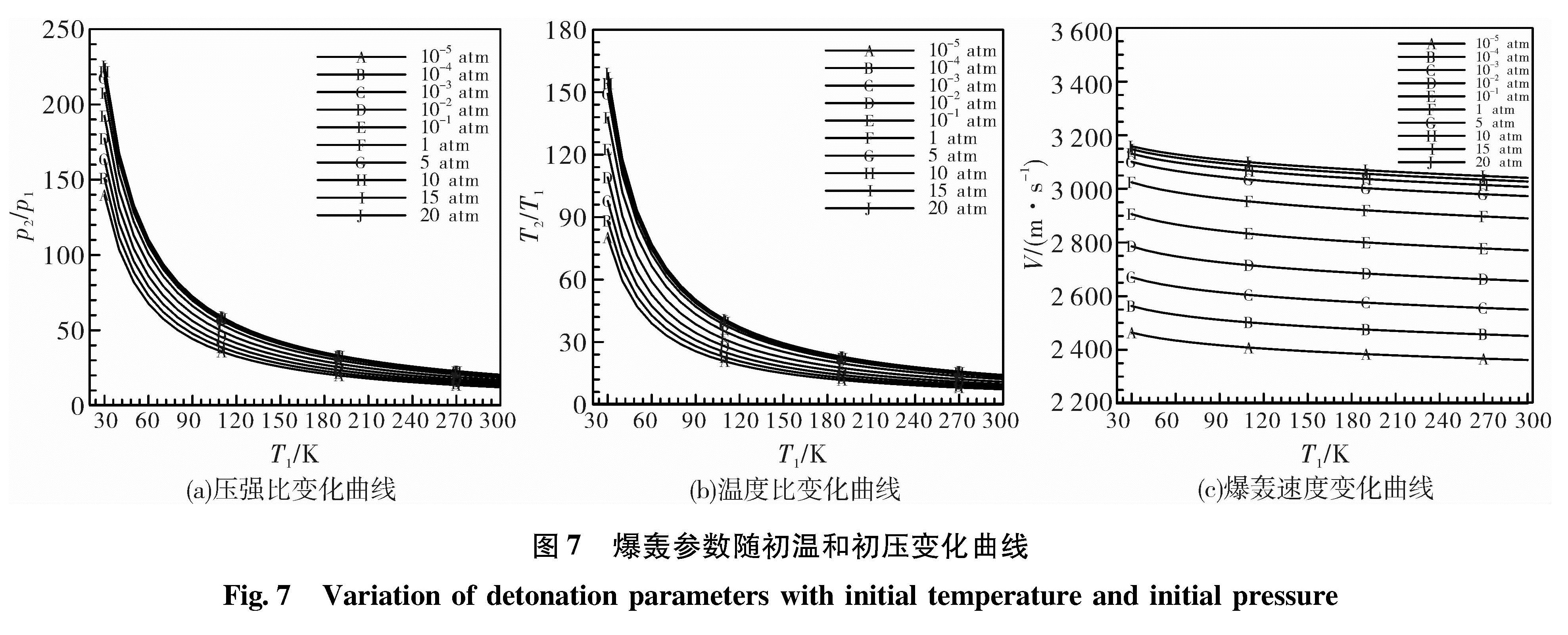
Fig.6 Variation of detonation parameters with mixing ratio and initial pressure2.2.2 初温、初压对爆轰参数的影响规律与前一节类似,为了分析初温、初压对爆轰参数的影响规律,需要固定另一个参数—混合比,这里采用化学当量混合比。初温T1范围取30～300 K,初压p1范围取10-5～20 atm。计算可得压比、温度比和爆轰速度的变化曲线(见图7)。由图7(a)和7(b)可知T1对压强与温度的影响非常大,T1由30 K增大到300 K,最大压比从220降低到20左右; 温度比与压比的变化趋势相同,比值从160降低到20左右。总的来看,温度与压强的变化近似于双曲关系。图7(c)表明随T1的增大,爆速略有降低,且p1越大,爆速越高。
图7 爆轰参数随初温和初压变化曲线
Fig.7 Variation of detonation parameters with initial temperature and initial pressure2.2.3 爆轰热力参数的变化规律由前面的分析得知,影响爆轰的最主要因素有三个:初温T1,初压p1与混合比K。下面分别选择一个变量定性分析其对爆轰热力参数的影响规律。
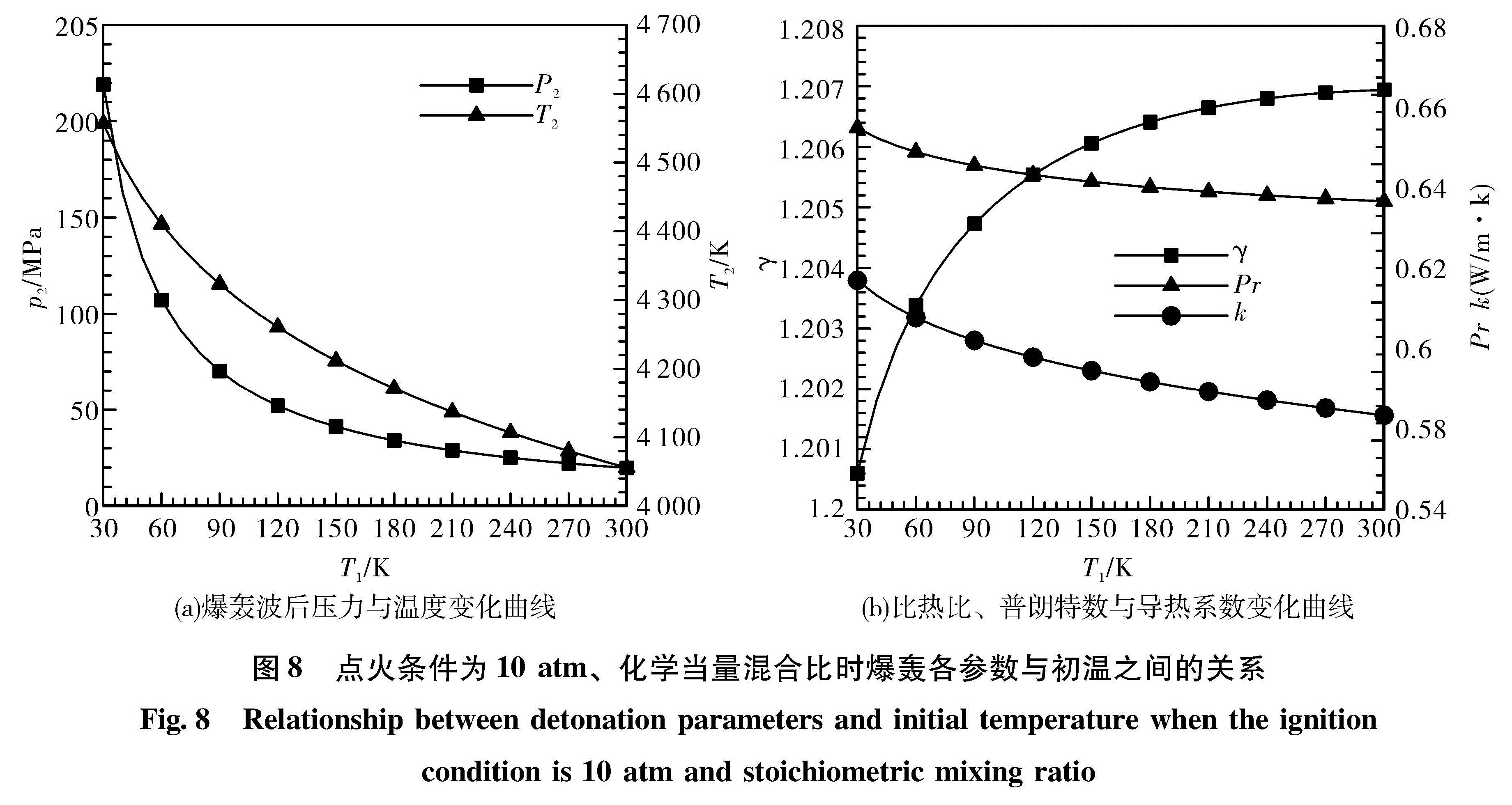
2.2.3.1 初温的影响选定p1为10 atm,K为当量混合比,T1变化范围为30～300 K时的热力参数如图8所示。爆轰后压力与温度随T1增大而减小,在低温时如30K,爆轰后压力可达220 MPa,温度在4500K以上,爆轰强度极大。且由爆轰后的混合气体成分也可以看出在该高温高压下,混合气体中H,O原子的摩尔数在1～3之间,说明此时存在较强的离解反应。γ随T1增大略有上升,而Pr与k值略有降低。
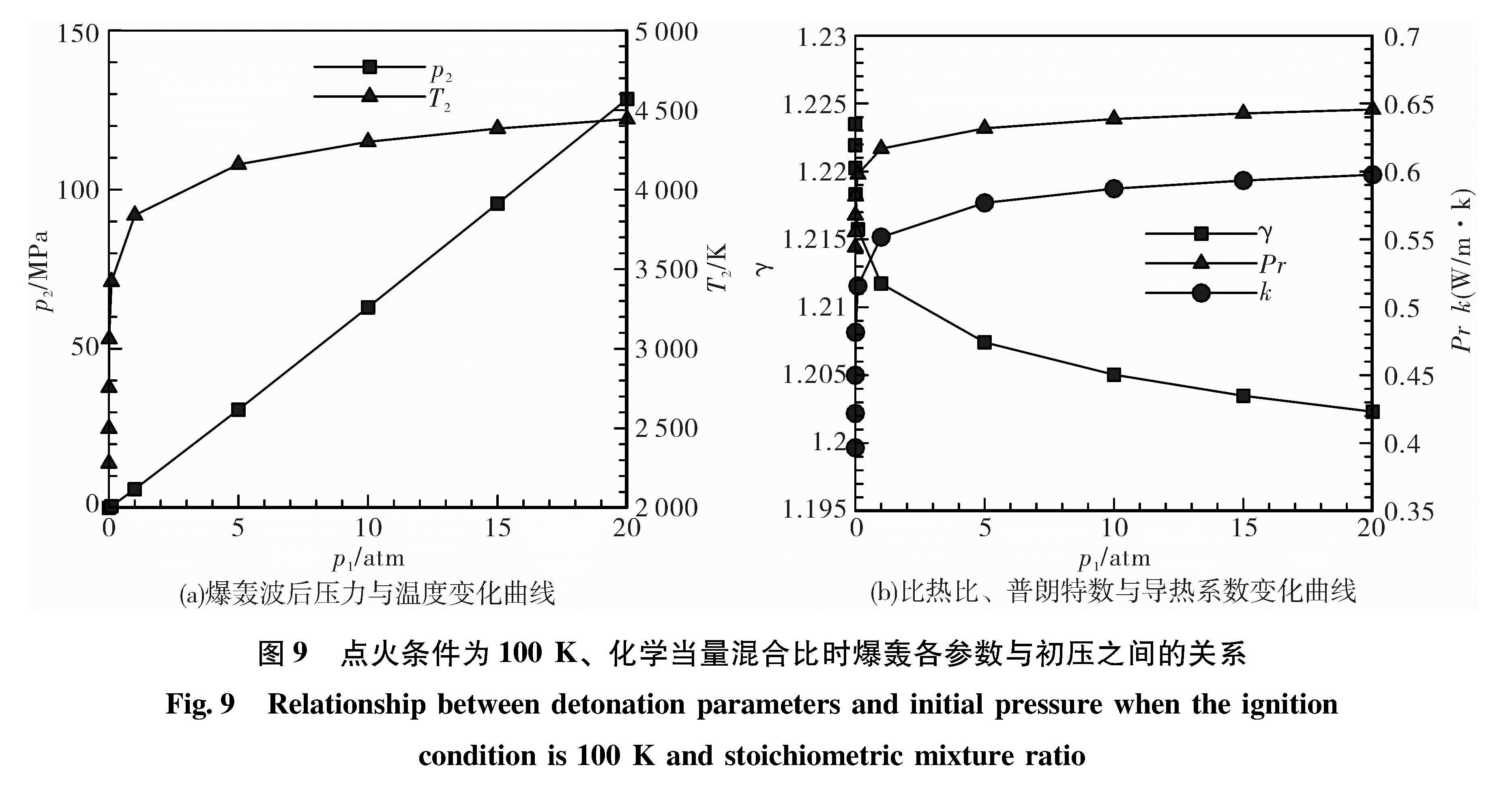
2.2.3.2 初压的影响选定T1为100 K,K为当量混合比,p1变化范围为10-5～20 atm时的热力参数如图9所示。
图8 点火条件为10 atm、化学当量混合比时爆轰各参数与初温之间的关系
Fig.8 Relationship between detonation parameters and initial temperature when the ignition condition is 10 atm and stoichiometric mixing ratio爆轰后压力与p1近似线性关系,最大为130 MPa,温度逐渐增大并稳定在4 500 K左右。γ随初温增大略有降低,而Pr与k值与之相反。
图9 点火条件为100 K、化学当量混合比时爆轰各参数与初压之间的关系
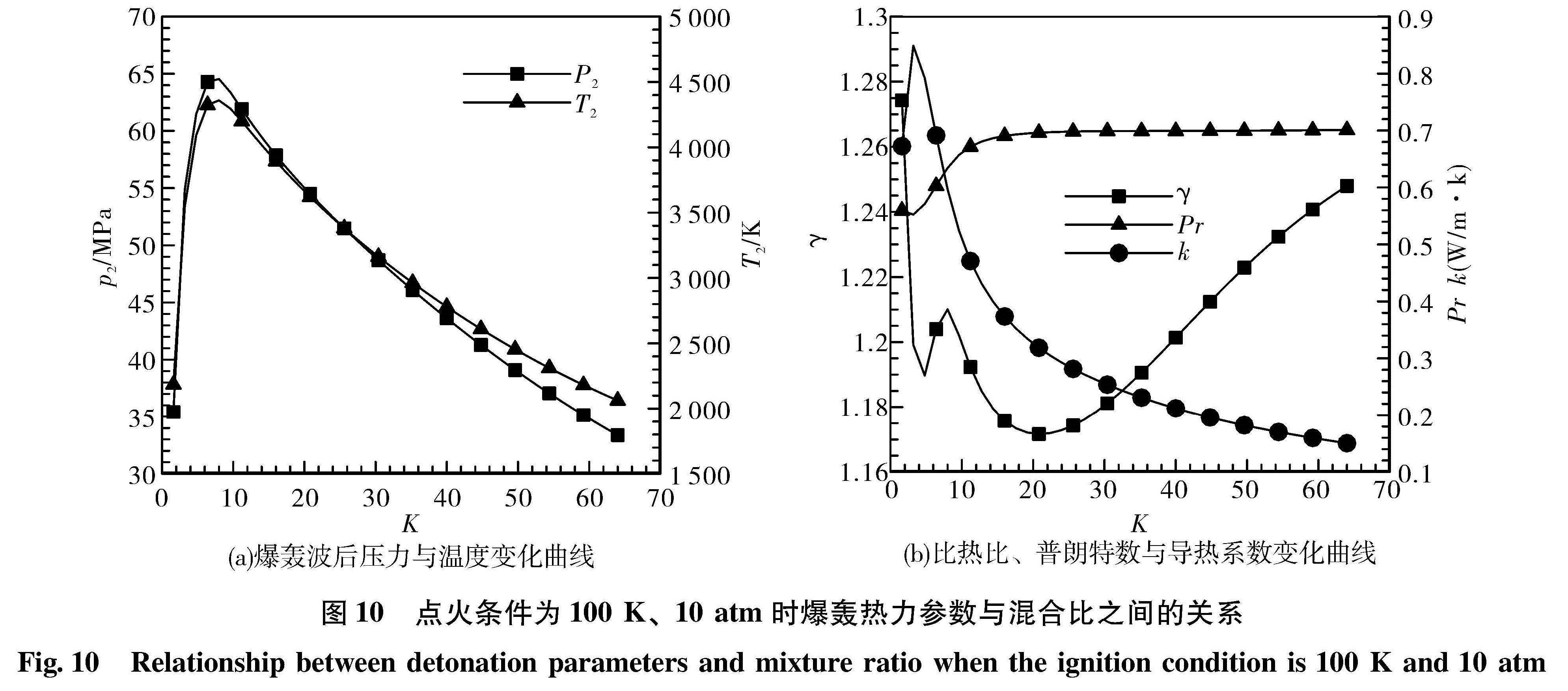
Fig.9 Relationship between detonation parameters and initial pressure when the ignition condition is 100 K and stoichiometric mixture ratio2.2.3.3 混合比的影响选定T1为100 K,p1为10 atm,K变化范围为2～64时热力参数如图 10所示。爆轰后压力和温度变化趋势一致,在当量比时有最大值,最大压力为65 MPa,最高温度为4 300 K。γ先减后增,k先增后减,而Pr稍有增大并稳定在0.7左右。
由以上三点分析可以看出初温与初压对爆轰热力参数的影响是单调的,即初温越低、初压越高爆轰后的压力与温度值越大,但比热比等热力参数随初压与初温的变化并不是简单的单调关系; 混合比的影响规律存在极值点,在当量混合比处爆轰强度最大; 低温爆轰压力可达220 MPa,温度高达4 500 K(见图8(a))。
图 10 点火条件为100 K、10 atm时爆轰热力参数与混合比之间的关系
Fig.10 Relationship between detonation parameters and mixture ratio when the ignition condition is 100 K and 10 atm2.3 爆轰规律总结计算结果表明,利用C-J理论可以较为准确的预测爆轰的一般规律。综合分析爆轰点火条件的影响规律,可以得出:1)决定爆轰强度的最主要因素为初温,初温越低,爆轰强度越大,尤其在低温区,压比与温度比的变化梯度很大; 2)越接近当量混合比爆轰强度越大; 3)初压越大,爆轰强度也越大; 4)爆速主要由混合比与初压决定,混合比越小,初压越大,爆速越高。
常用氢氧发动机点火压力为1～2 MPa,点火温度极低,由于推进剂掺混的不均匀性,使得点火处的混合比很难确定。如图8所示,当温度为30 K时,此时处于气氢与液氧状态,取点火压力为1 MPa,混合比为8,若发生爆轰,此时压力可达220 MPa,温度高达4 500 K,爆轰强度极大。并且爆轰速度高达3 000 m/s,爆轰波可以在极短的时间内(微秒量级)传遍发动机,甚至会导致发动机的结构破坏。
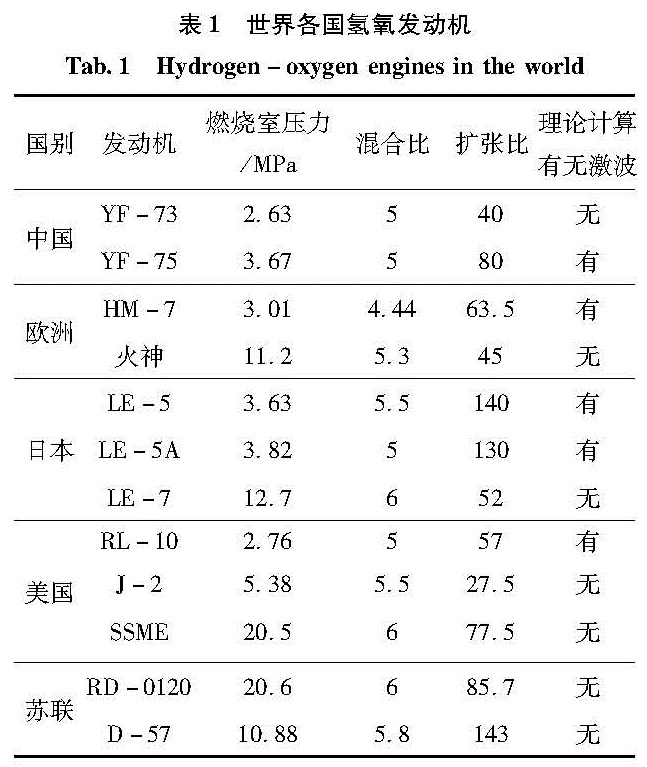
通过对世界各国诸多大推力氢氧发动机型号按照冻结流方式进行初步分析,可以发现,由于喷管扩张比较大,很多发动机在地面试车时,喷管扩张段内可能会产生激波。这一点从表1列出的世界各国的发动机混合比、燃烧室压力、扩张比以及有无激波(环境压力为1 atm条件下)等相关数据可以看出。 因此,研究大扩张比喷管中的激波,具有一定的工程实际意义。
表1 世界各国氢氧发动机
Tab.1 Hydrogen-oxygen engines in the world本节将计算分析推进剂混合比和燃烧室压力对激波位置及其热力参数影响的一般规律,而不是限于研究某个特定发动机型号。虽然按照冻结流的方式,可以获得一个相对可靠的初步计算结果,但是氢氧燃烧的高温产物在喷管中流动时,由于压力和温度的不断改变,化学平衡也会相应不断地移动。因此,为了获得更为理想的计算结果,在一维管流模型基础上引入热化学反应的影响,采用平衡流动模型来计算热力参数。平衡组分的计算方法有平衡常数法、最小Gibbs自由能法和元素势法,目前常用的计算机程序有基于最小Gibbs自由能原理的CEA程序[23]和基于元素势法的STANJAN程序[24]。相比于以上两种计算程序,布林克莱法计算平衡组分时,气相组分不会出现负值; 开始选取的初始值较少,计算结果较容易接近真实情况; 迭代时用的方程数少,计算时间相对较省[25]。所以本文选择布林克莱法来进行平衡流计算,平衡组分包括H2,O2,H2O,OH,H及O六种。
1.1 计算方法基于一维定常可压缩流体在拉伐尔喷管内的流动模型,激波的计算过程如下:根据引入热化学反应后的激波理论计算公式与过膨胀喷管扩张段内激波后的反应流状态(激波后的气流到喷管出口处完全膨胀),通过迭代使得激波位置参数满足喷管内气流流动状态,确定激波位置,及激波影响效果和波后热力参数[26]。计算开始时假定激波位置在喷管中间,然后采用二分法进行迭代,计算出激波的位置。详细的计算求解过程见图1。
由一维定常可压缩流体在激波前后的连续方程、动量方程、能量方程可导出:
(p2)/(p1)=1-((ρ1u12)/(p1))((ρ1)/(ρ2)-1)(1)
h2=h1+((u12)/2)[1-((ρ1)/(ρ2))2](2)
等号右侧用总压p*和总焓h*代替,方程变为:
p*-(p2)/(p1)=0(3)
h*-h2=0(4)
将原变量取对数,新的自变量变为ln(p2)/(p1),ln(T2)/(T1)。
采用Newton-Raphon迭代法求解该二元非线性方程组,可得迭代公式为:
((p*-(p2)/(p1)))/(ln((p2)/(p1)))Δln(p2)/(p1)+((p*-(p2)/(p1)))/(ln((T2)/(T1)))Δln(T2)/(T1)=(p2)/(p1)-p*(5)
(((h*-h2)/R))/(ln((p2)/(p1)))Δln(p2)/(p1)+(((h*-h2)/R))/(ln((T2)/(T1)))Δln(T2)/(T1)=(h2-h*)/R(6)
{(Δln(p2)/(p1))k=ln((p2)/(p1))k+1-ln((p2)/(p1))k
(Δln(T2)/(T1))k=ln((T2)/(T1))k+1-ln((T2)/(T1))k(7)
式中:p为压力; T为温度; ρ为密度; h为总焓(化学能+物质的焓); R为气体常数; 下角标1为激波前参数; 下角标2为激波后参数。详细推导过程见参考文献[26]。
注:图中的虚线箭头表示调用关系。
图1 激波计算流程图
Fig.1 Flow chart of shock wave calculation1.2 计算结果分析影响喷管中激波位置及热力参数的主要因素有三个:燃烧室压力、燃烧室温度和喷管出口压力。由于燃烧室温度主要由燃烧室压力和推进剂混合比决定,并且主要研究的是发动机在地面附近的工作情况,喷管出口压力始终取1个大气压,所以接下来主要计算和分析激波随燃烧室压力和推进剂混合比的变化规律。
分析计算主要从如下三个方面来进行:1)计算和分析热化学反应对计算结果的影响; 2)给定混合比下,计算和分析燃烧室压力对激波位置以及各热力参数的影响规律; 3)给定燃烧室压力,计算和分析混合比对激波位置以及各热力参数的影响规律。主要针对压力、温度、密度比与比热比、普朗特数、导热系数等热力参数值进行分析(文中将统一使用γ,Pr,k分别为比热比、普朗特数、导热系数)。
1.2.1 热化学反应对计算结果的影响将考虑热化学反应时的激波前后热力参数与常用激波理论(朗金-雨贡纽关系式)计算结果对比。理论公式如下:
(p2)/(p1)=(2k)/(k+1)Ma21-(k-1)/(k+1)(8)
(T2)/(T1)=1/(Ma21)(2/(k+1))2(kMa21-(k-1)/2)(1+(k-1)/2Ma21)(9)
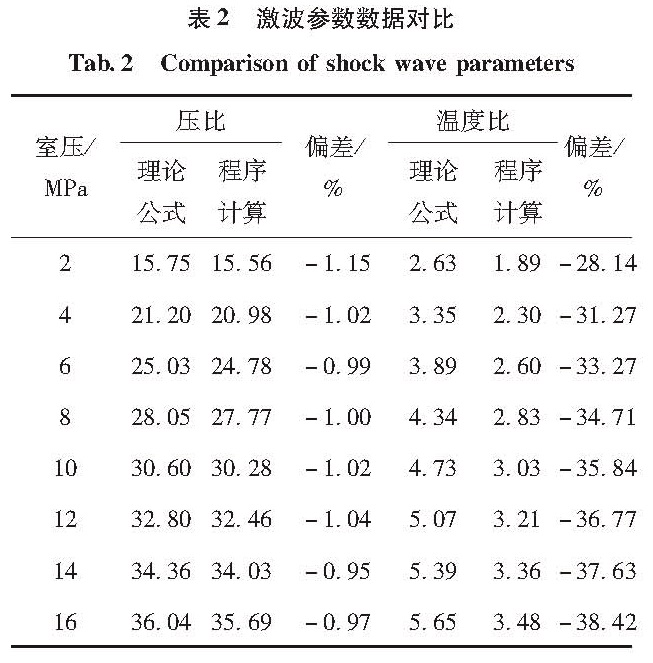
参考表1中氢氧发动机参数,取混合比为6、喷管出口压力为一个大气压时的计算结果与经典激波理论对比见表2。因为经典激波理论计算中采用冻结流方法,故选择两个具有代表性的宏观参数压比与温度比作为对照。
表2 激波参数数据对比
Tab.2 Comparison of shock wave parameters表2数据表明,考虑热力反应的计算结果与理论公式计算的结果相比,压强基本一致,相对偏差在1%以内,而温度偏差较大,且随室压增大而增大,最大为38%。可见,考虑热化学反应与冻结流计算的结果存在较大差异,所以在计算激波参数时考虑热化学反应是必要的。
由图2(b)可以看出,随着压力的增大,平衡气体组分中除了H2O以外的组分含量均有所上升,而生成H,O的离解反应以及氢氧生成水的逆反应都是吸热的,这就使得相比于冻结状态下能量会被消耗掉,因此计算得到的温度比要比经典激波理论(冻结流)计算的值偏低。
1.2.2 燃烧室压力的影响规律参照表1中数据,混合比K取为6,燃烧室压p取2～16 MPa时激波位置、激波作用下的气体成分、压力与温度比值以及比热比等热力参数的变化曲线如图2所示。由图2(a)可以看出激波位置与室压线性相关,室压越大,激波位置越靠外。图2(b)所示气体组分中,除了水的含量下降,其余组分含量均有所上升,且与室压大小关系不大。图2(c)表明室压越大,激波作用下的压比、温度比与密度比越大。由图2(d)可知激波后γ值变小,k增大,且室压越大激波前后数值差越大,Pr基本不变。
图2 燃烧室室压对激波各参数的影响
Fig.2 Effects of chamber pressure on shock wave parameters1.2.3 混合比的影响规律室压p为2MPa时,混合比K取4～16时激波位置、激波作用下的气体成分、压力与温度比值以及比热比等热力参数的变化曲线如图3所示。由图3(a)可以看出在近化学当量混合比时激波位置略靠外,但位置总体差异不大。图3(b)所示激波前后气体组分变化表明,经过激波后,气体成分中H2O的含量降低,其余组分含量增加。由图3(c)可知压比与温度比在当量混合比时较小,密度比略有升高。从图3(d)可以看出γ受混合比影响较大,在化学当量混合比处有最小值,Pr与k在化学当量混合比处略有增大。
图3 混合比对激波各参数的影响
Fig.3 Influence of mixture ratio on shock wave parameters1.3 激波规律总结通过计算验证发现,考虑热化学反应时激波后温度比有较大差异。压强与混合比的计算结果对比可得,压强影响下的参数变化是单向的,而混合比的影响则更为复杂,一般在化学当量混合比时有极值点。
由表1中的数据可以看出,氢氧发动机中,燃烧室室压多为2～20 MPa,喷管的扩张比多在50以上,最大可到140。在地面试车以及低空工作阶段,出口反压约为大气压强,此时在扩张段内可能会产生激波。激波影响下,压力与温度会突跃,对喷管造成不稳定冲击,对其结构强度与工作效能产生很大影响,故分析喷管内的激波具有一定的实际意义。
