随着超燃冲压发动机和火箭冲压组合发动机技术的不断成熟,其应用从导弹武器向高超声速飞机、天地往返运输系统等领域拓展,发动机规模不断扩大^[1]。同时,发动机流道截面不再局限于矩形,圆形及椭圆形截面流道在设计、结构及防热等方面的优势逐渐得到认可^[2]。此外,面向不同的应用背景,发动机的尺度差异巨大。要发展大尺度发动机,就需要深入研究发动机尺度对关键组件的影响。

隔离段是超燃冲压发动机和火箭冲压组合发动机的重要部件,用来隔离燃烧室燃烧形成的压力升高对进气系统的影响^[3],使发动机在较宽的马赫数范围内稳定工作。如果隔离段不能承受压力升高可能导致进气系统不起动,引起发动机推力减小和工作性能恶化^[4]。

国内外研究机构在不同截面形状隔离段的流动特征、抗反压特性及裕度控制等方面进行了大量的理论仿真和试验研究^[5-8]。文献[9～15]分析总结出了矩形和圆形截面隔离段内分布同流场参数之间的经验关系式。文献[9～12]给出的关系式可以用来计算沿激波串的压力分布,也可以依据这些一维关系式估算激波串长度。文献[13]和文献[14]的方法可一维求解伴随传热传质过程的非等截面管道内扩压过程,方法适用范围更广。对于大尺度发动机,由于隔离段入口位置流动参数分布、边界层与小尺度发动机存在明显的不同,隔离段内的压力分布规律可能发生变化,隔离段尺度也不可能完全按照几何缩放。

本文采用文献[13]和文献[14]提出的非等截面管道一维扩压流动模型,分析了不同尺度矩形截面和圆形截面隔离段内的扩压过程和缩尺关系。

选用了Auslender^[13-14]提出的稳态准一维隔离段分析模型。模型将隔离段扩压区域分成分离区和核心区,形成了如下方程组:

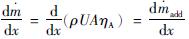(1)

(dF)/(dx)=(d)/(dx)(pA+ρU²Aη_F)=p_wall(dA)/(dx)+(dD)/(dx)+(dF_add)/(dx)(2)

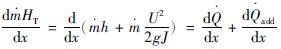(3)

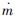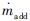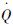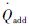式中:为质量流量; x为轴向距离; ρ为密度; U为轴向速度; η_A为分离流动中的质量畸变指数; 为添加的质量; F为动量; p为压力; η_F为分离流动中的动量畸变指数; p_wall为壁面压力; D为阻力的粘性项; F_add为动量添加量; H_T为气流的总焓; h为气流的静焓; g为重力加速度; J为守恒因子;为热量; 为传热量。

对于准一维问题,η_A和η_F相对难以确定,将该方法应用于隔离段问题时,假设这两个参数相同,这个简化使得仅需方程(4)即可封闭式(1)～式(3)所示方程组:

(dp)/(dx)=(ρU²)/(D_H)(Re_θ0)1/4≈C/(D_H)C_f0((ρU²)/2)(4)

式中:D_H为水力直径; C为常数; Re_θ0为以分离起始点动量厚度定义的雷诺数; C_f0为分离起始点的摩擦系数。当给定这些参数后,该方程组可以在不给定下游边界条件的情况下预测轴向静压分布。

为了验证该方法(简称为模型一)对隔离段压力分布的计算准确性,以小尺度燃烧室Ma=6直连试验环境计算了隔离段压力分布。同时还用文献[4]给出的激波串内压力分布与流场参数之间的经验关系式(简称为模型二)计算了隔离段压力分布,模型为:

(x(Ma²₁-1)Re^1/4_θ)/(H^1/2θ^1/2)=50((p₂)/(p₁)-1)+170((p₂)/(p₁)-1)²(5)

式中:Ma为入口马赫数; x为沿流向距离; H为隔离段高度; θ为附面层动量厚度; p₂为出口压力; p₁为入口压力。

图1对比了两种方法获得的压力分布及直连试验数据。

图1 Ma=6状态下隔离段壁面压力分布对比
Fig.1 Wall pressure distribution of isolator at Ma=6

从图1可见,模型一获得的压力分布与试验数据较为接近,能够较好地模拟隔离段内的扩压过程。

以不同尺度发动机在相同飞行马赫数、高度、攻角及侧滑角条件下的流量来表征发动机的尺度关系。取入口宽0.23 m、高0.06 m的矩形截面隔离段为基准,定义为1×。其他尺度矩形截面隔离段入口尺寸按比例放大,不同尺度圆形截面隔离段的入口面积与矩形截面的隔离段保持一致。表1给出了不同尺度隔离段的入口尺寸。图2给出了不同尺度隔离段的入口示意图。

表1 隔离段的入口尺寸
Tab.1 Entrance dimensions of rectangular and circular isolator

图2 矩形和圆形截面隔离段入口面积示意图
Fig.2 Comparison of entrance area for rectangular and circular isolator

选择表1中1×、10×和100×的隔离段进行尺度效应分析。虽然矩形截面隔离段和圆形截面隔离段对应的发动机进气系统喉部参数存在一定差异性,但在理论分析阶段可视为一致。本文选择Ma=4和19.8 km作为隔离段尺度效应分析的状态点,其他状态点的情况与之类似。按照研究经验,Ma=4条件下隔离段压比能够达到正激波压比的70%,因此选择70%正激波压比作为隔离段压力分布的约束,将达到70%正激波压比的激波串长度视为所需的隔离段长度。Ma=4状态下隔离段入口参数见表2。

表2 Ma=4状态下隔离段入口参数
Tab.2 Entrance parameters of isolator at Ma=4

从表2可见,由于不同尺度隔离段入口的边界层厚度不同,该位置的参数略有不同。此外,摩擦系数C_f0与边界层发展情况密切相关,随隔离段的发动机的尺度变化,按照二元进气道边界层理论计算得到矩形隔离段的C_f0,由于圆形截面隔离段的C_f0求解非常困难,这里沿用矩形隔离段的C_f0。

采用上述算法和表2所列参数,计算了不同尺度矩形截面隔离段的压力分布,如图3所示。为了研究摩擦系数C_f0对隔离段压力分布的影响,在图3中同时给出了采用1×隔离段摩擦系数C_f0,1×计算得到的10×和100×压力分布,为了方便比较,用达到70%正激波压比时的激波串长度x_ref进行了量纲归一化处理。从图3可见,采用1×隔离段摩擦系数C_f0,1×计算得到的1×、10×和100×量纲为一的压力分布几乎完全重合; 10×隔离段和100×隔离段的量纲为一的长度相对1×隔离段的量纲为一的长度长出13%和32%,说明对于给定的飞行状态,隔离段长度与摩擦系数C_f0密切相关。

图3 矩形截面隔离段压力分布
Fig.3 Relative wall pressure distribution of rectangular isolator

图4给出了不同尺度圆形截面隔离段的压力分布。从图4可见,圆形截面隔离段内的压力分布趋势与矩形截面隔离段一致; 10×隔离段和100×隔离段的量纲为一的长度相对1×隔离段的量纲为一的长度长出9%和23%,相对变化量较矩形隔离段小。

图5对比了不同尺度、不同截面形状的隔离段的压力分布。从图5可见,隔离段尺度越大,隔离段内压力升高过程越平缓; 隔离段长度不与入口水力直径呈线性关系,即隔离段长度不能几何缩比; 相同入口水力直径的隔离段,在给定的压升条件下,圆形截面隔离段的长度更长,1×、10×和100×的圆形截面隔离段长度较矩形截面隔离段长49%、39%和38%。按照参考文献[10],矩形截面隔离段长度与宽高比有密切关系,因此圆形截面隔离段长度与矩形截面隔离段长度之间的差异与矩形截面隔离段宽高比也相关。

图4 圆形截面隔离段压力分布
Fig.4 Relative wall pressure distribution of circular isolator

图5 隔离段长度比较
Fig.5 Comparison of isolator length

本文利用稳态准一维隔离段分析模型,对不同尺度的矩形截面和圆形截面隔离段的压力分布进行了计算分析,发现隔离段入口的摩擦系数影响隔离段压力分布规律; 在给定的压升条件下,相同尺度的圆形截面隔离段比矩形截面隔离段长; 隔离段长度不与入口水力直径呈线性关系,即隔离段长度不能几何缩比。