基金项目:国家自然科学基金(11602186)
作者简介:许志宇(1989—),男,博士,研究领域为液体火箭发动机调节与控制
(1.西安航天动力研究所,陕西 西安 710100;2.液体火箭发动机技术重点实验室,陕西 西安 710100;3.航天推进技术研究院,陕西 西安 710100)
(1.Xi'an Aerospace Propulsion Institute, Xi'an 710100, China; 2.Science and Technology on Liquid Rocket Engine Laboratory, Xi'an 710100, China; 3.Academy of Aerospace Propulsion Technology, Xi'an 710100, China)
为了克服传统谱方法计算水击问题的数值振荡,选择具有紧支撑特性的样条小波代替传统的基函数,建立了一维流体运动方程的自适应小波配点计算格式,并对有摩擦和无摩擦的一维管路水击问题进行了数值计算,获得了水击波的传播过程。结果 表明:小波配点法能够准确计算水击波的传播过程,在水击波波阵面处,不会因高分辨率出现剧烈的数值振荡现象,精度和分辨率可以同时提高; 自适应算法能够自动捕捉水击波位置,并在水击波局部区域采用高分辨率计算,而在梯度较小区域降低分辨率计算,在保障精度和分辨率的前提下,显著节约计算量。
In order to restrain the numerical oscillation of computing water-hammer problem using the traditional spectral method, an Adaptive Wavelet Collocation Method(AWCM)based on the compactly supported spline wavelet was established for the one-dimensional fluid motion equation.The water-hammer problems of one-dimensional pipeline with friction and without friction were numerically computed, and the propagation process of water-hammer wave was obtained.The results show that the Adaptive Wavelet Collocation Method can accurately compute the propagating process of water-hammer wave.At the wavefront, there will be no sharp numerical oscillation phenomenon due to the high resolution, and both the accuracy and resolution can be improved simultaneously.In addition, the method can automatically capture the position of water-hammer wave, and adopt the high resolution in the local area of water-hammer wave while reduce the resolution in the small gradient area, which save the computational cost largely on the premise of guaranteeing the accuracy and resolution.
高速流动的液体因阀门突然关闭或泵骤停会产生水击现象。如果水击压力过高、剧烈,可能造成液压元件或管路破坏、液体泄漏等问题。
水击的数值计算方法包括有限元法、有限差分法、有限体积法和谱方法等[1-4]。其中,谱方法选择适当的基函数逼近计算域内的函数,然后结合加权余量法求解偏微分方程,具有精度高、收敛性好的优点。但不论是Fourier级数、Chebyshev或Legendre多项式,在计算域内均不具有紧支撑特性,当求解水击这一类具有局部奇异性问题时,分辨率越高,产生的数值振荡越严重,需要配合使用滤波才能消除[1]。
小波数值方法是基于计算流体力学中精确计算湍流和捕捉激波发展起来的高精度高分辨率方法,属于谱方法范畴,主要有小波-迦辽金法(Wavelet-Galerkin Method)和小波配点法(Wavelet Collocation Method)。由于小波函数具有紧支撑特性,因此相对于Fourier等基函数,能有效抑制数值振荡; 此外,根据多分辨分析,可以采用自适应方法自动提高或降低分辨率,在保障精度的前提下可减少计算量,适合求解局部奇异性问题。文献[5]详细介绍了利用3次样条小波有限元法求解水击问题的理论,但并未开展数值计算。文献[6]将区间样条小波应用于太阳能帆板的轨迹优化。文献[7]详细讨论了利用样条小波求解初边值问题,文献[8]利用小波数值方法求解多维偏微分方程,文献[9-14]利用自适应小波配点法求解双曲守恒律方程,用于计算激波、爆轰波等间断问题,精度和分辨率均较高,文献[15-16]将小波方法应用于湍流数值模拟,可有效降低计算量。
本文采用自适应小波配点法(Adaptive Wavelet Collocation Method, AWCM)对一维管路水击进行数值计算,给出了小波数值方法的原理、计算过程和结果,分析了小波数值方法计算水击问题的能力和特点。
根据多分辨分析(MultiResolution Analysis, MRA)理论可知,尺度函数φ(x)伸缩平移变换张成的闭子空间Vj构成一组多分辨分析,尺度函数对应的小波函数ψ(x)通过伸缩平移变换张成的小波空间Wj构成尺度空间Vj的正交补空间。可表示为
φj,k(x)=2j/2φ(2jx-k)(1)
ψj,k(x)=2j/2(2jx-k)(2)
Vj=Vj-1Wj-1(3)
设函数f(x)∈L2(R),根据式(3)可得f(x)的多尺度分解
f(x)=∑k∈ZSj0,kφj0,k(x)+∑∞j=j0∑k∈Zdj,kψj,k(x)(4)
式中s,d分别为尺度函数系数和小波系数。小波系数的绝对值越大表明f(x)在相应尺度的分量越大。
实际上不可能对f(x)作无限分解,因此尺度因子j只能取至某个上限J-1,使分辨率达到2-J,式(4)则近似表示为
fVJ(x)=∑k∈ZSj0,kφj0,k(x)+∑J-1j=j0∑k∈Zdj,kψj,k(x)(5)
对于水击这一类问题,解通常仅在局部区域不连续或梯度较大,而在其他区域相对平缓,相应的小波系数均非常小。因此式(5)可以根据小波系数相对于阈值ε的大小分为两部分[7]
f(x)=f≥(x)+f<(x)(6)
其中
f≥(x)=∑k∈ZSj0,kφj0,k(x)+
∑J-1j=j0∑|dj,k|≥εdj,kψj,k(x)(7)
f<(x)=∑J-1j=j0∑|dj,k|≥εdj,kψj,k(x)(8)
Donoho(1992年)证明,对于正则方程,舍去式(8)系数较小的小波,逼近的误差上限为

根据小波系数的大小判断变化剧烈的局部位置,并选择适当的阈值对局部区域增加或降低分辨率的方法称为自适应算法。Mallat分解首先从最细尺度向尺度函数空间分解,得到尺度函数系数,然后根据双尺度方程
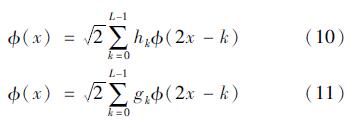
利用快速算法,逐步计算上一尺度的尺度函数系数和小波系数,如果小波系数的绝对值大于设定的阈值,则保留该小波,如果小于设定的阈值,则删除该小波[5-8]。这种自适应算法效率高,但对于求解发展方程仍有不足。由于随着时间推进,奇异位置发生移动,为了更好捕捉奇异位置和减小误差,应适当保留奇异位置附近的配点,使得奇异位置移动后仍能保持分辨率[7]。
小波配点法以小波分解为基础,通过式(5)计算偏微分方程中的空间导数项,一阶导数
(d)/(dx)fVJ(x)=2j0∑k∈ZSj0,kφ'j0,k(x)+
∑J-1j=j02j∑J-1k∈Zdj,kΨ'j,k(x)(12)
从而化偏微分方程为关于时间的常微分方程[5]。然后利用Euler法、R-K法等常微分方程的数值方法求解。
假设流体在管路内作一维绝热流动,考虑壁面摩擦,无量纲的一维流动方程为[1]
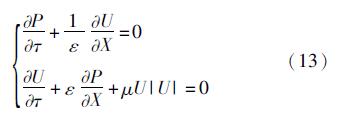
其中
P=p/pT
U=u/a
X=x/L
τ=ta/L
式中:P, U, X及τ分别为无量纲的压力、速度、位置及时间; 系数ε=p0/(ρa),μ=fL/(2D); pT和p0分别为入口压力和管中初始压力; L和D分别为管长和管径; ρ和a分别为流体密度和声速。
时间离散采用Euler法,因此式(13)的半离散格式为
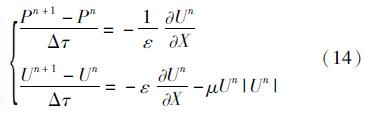
式中压力和速度采用小波分解表达式
PVJ=∑k∈ZSP0,kφ0,k(x)+∑J-1j=0∑k∈ZdPj,kψj,k(x)(15)
UVJ=∑k∈ZSU0,kφ0,k(x)+∑J-1j=0∑k∈ZdUj,kψj,k(x)(16)
根据式(12)计算出压力和速度的空间一阶导数,一并代回式(14)中,选取合适的时间步长Δτ,求解下一时刻的压力和速度分布。重复上述过程便可求解各时刻的物理场。
小波变换定义在整个实数域(-∞,+∞),而实际问题均属于有限域[L,R]。截断(-∞,L)和(R,+∞)范围内的小波,会在边界处造成较大误差,使得边界处小波系数产生异常、精度降低,即边界效应。本文采用边界延拓的方法保障边界精度,使边界效应不在真实的物理边界处发生。
边界延拓的关键在于给延拓的部分赋值。对于实际问题,根据边界条件给定,使延拓部分具有相应边界条件的物理意义。阀门关闭形成刚性壁面条件,即壁面处的速度为0,压力通过式(14)计算,而延拓部分与关于壁面对称部分的速度大小相等、方向相反,压力和温度等标量大小相等。对于压力入口,延拓区域的压力设定为与入口压力相同,速度则通过式(14)计算。
尺度函数和小波函数的支集一般为整数域,为了方便进行小波分解和建立统一的计算格式,计算域[L,R]设定为正整数作为基础域,对于实际问题进行坐标变换。本文选用的小波为支集为4的四阶三次样条小波,基础域为[0,16]。
选择水平直管路阀门瞬间关闭产生水击的模型(图1)进行计算。管路参数和初边值如表1所示[1],无量纲的初始流速U0=5.67*10-3,当t>0,阀端流速设置为0,以模拟阀门瞬间关闭。
首先针对无损水击进行计算。由于不考虑管路沿程损失,管路中产生的水击为周期T=4L/a的方波,根据如科夫斯基公式,可求得完全水击压力的理论值
Δp=Δuρa(17)
由于无压力损失,因此管中稳态压力等于入口压力pT,初始流速假设与摩擦系数f=0.018时相同,即U0=5.67*10-3,根据式(17)可得Δp≈0.544,则水击的波峰和波谷分别为1.544和0.456。
调整阈值ε时,由于压力和速度的值以及变化范围差别很大,因此设定εU=εU0,εP=εP0。固定时间步长后,计算精度依赖于最大尺度因子和阈值,当尺度因子足够大,则精度主要受阈值大小影响。数值试验表明,同一时刻速度场的配点比压力场配点多,并且速度场配点基本包含压力场所有配点。如果尺度因子较小,可能会使速度场的计算精度达不到要求。
当取阈值ε=5*10-5(εU=εU0,εP=εP0),尺度因子J=6,时间步长Δτ=2*10-7,计算无摩擦损失的水击,可以得到较好的结果,如图2(a)~图2(d)所示。压力稳定后,统计前3个周期(记为T1,T2和T3)的水击波峰和波谷的平均值,如表2所示,水击压力平均值与理论值的误差小于0.9%。时间和空间的大梯度处分辨率较高,且无明显数值振荡。由于时间积分采用的是只有一阶精度的Euler格式,计算精度和稳定性对阈值、尺度因子以及时间步长要求严格,数值试验表明,为了使计算稳定,参数应满足:ε<0.001,J>3,Δτ=1*10-6。
图2(a)表明,在第一个T/2内,压力的数值振荡较小,随后数值振荡相对明显。由于阀前速度恒为0,因此图2(b)表示的阀前速度计算值同时代表速度的计算误差。阀前速度的计算误差同时显示,在第一个周期内计算误差较小,约为1*10-8,在随后的周期内最大误差保持在4*10-5以内。真实的流体管路有一定摩擦损失,造成水击压力逐渐下降。假定摩擦系数f=0.018,并取J=6,ε=5*10-5,Δτ=2*10-7,计算结果如图3所示。
自适应小波配点法能够自动判断梯度的大小和位置,自动在大梯度处增加配点,并删除平稳区域内对计算精度影响较小的配点,在保证整个计算域内均达到设定精度的前提下减少配点数,从而减小计算量。因此在梯度较大的位置配点密集,而在变化平缓的位置配点稀疏。图4给出了不同时刻压力场配点分布和配点数(f=0.018,J=6,ε=5*10-5,Δτ=2*10-7),为了和小波空间W0(下标为0)区分,尺度空间V0以-1表示。对比图2(c),可以看出配点加密的位置对应水击波的波阵面,表明依据小波系数能够准确判断局部奇异性的位置。
图4(c)表明,根据初始条件,压力初值处处为1,数值随空间无变化,因此仅需25个配点,水击发展初期间断较强,所需配点数较多,约为125,随着水击波的发展,梯度略有减小,不同时刻所需配点数在105附近,而不采用自适应算法所需均匀配点数为513,因此压缩比约为4.89,节省了约80%的迭代计算量。
采用自适应小波配点法对一维管路水击问题进行了数值计算,结果表明:
1)小波配点法能够准确计算水击波的传播过程,在水击波波阵面处,不会因高分辨率出现剧烈的数值振荡现象,精度和分辨率可以同时提高。
2)自适应算法能够自动捕捉水击波位置并采用高分辨率计算,而在梯度较小区域降低分辨率,在保障精度和分辨率的前提下,显著节约计算量。
本文的小波分解和自适应方法均针对空间,无法控制时间误差。后续可采用时间-空间同步自适应方法,在局部变化剧烈的位置采用更精细的时间积分,从而控制时间积分过程产生的误差。