基金项目:国家重点基础研究发展计划(613321)
作者简介:杨宝锋(1989—),男,博士,研究领域为液体火箭发动机涡轮泵技术
(1.液体火箭发动机技术重点实验室,陕西 西安 710100; 2.西安航天动力研究所,陕西 西安 710100; 3.航天推进技术研究院,陕西 西安 710100)
(1.Science and Technology on Liquid Rocket Engine Laboratory, Xi'an 710100, China; 2.Xi'an Aerospace Propulsion Institute, Xi'an 710100, China; 3.Academy of Aerospace Propulsion Technology, Xi'an 710100, China)
turbopump; seal; large eccentricity; large disturbance; Bulk-Flow; computational fluid dynamics; dynamic characteristics
为获得大偏心以及大扰动下涡轮泵浮动环密封的转子动力特性,采用修正的Bulk-Flow模型和CFD准稳态法进行了研究。通过试验数据验证了两种方法的求解精度及可靠性,获得了不同静偏心以及扰动量下密封动特性系数的变化规律。结果 表明:修正的Bulk-Flow模型和CFD准稳态法均能较好地预测密封动特性系数,且CFD法具有更高的求解精度; 对于高压高转速涡轮泵,浮动环密封引入的刚度与滚动轴承刚度量级相当,其对转子系统动力学特性影响不应忽略; 大偏心下密封各动特性系数显著增大,而大扰动下,各系数与扰动量之间呈现出复杂的非线性关系。
A revised Bulk-Flow model and the quasi-steady CFD method were adopted to investigate the rotordynamic characteristics of a turbopump floating ring seal under large eccentricities and disturbances.The precision and reliability of these two methods were verified by the seal test data and the variation of the rotordynamic characteristics of the seal under different eccentricities and disturbances were obtained.Results show that the revised Bulk-Flow model and the CFD method can effectively predict the rotordynamic coefficients of seals and the CFD method presents better accuracy.For high-pressure-speed turbopumps, the stiffness introduced by a floating ring seal is comparable to the stiffness of the rolling bearing, thus the influence of the seal on rotor dynamic characteristics should not be ignored.The rotordynamic coefficients increase significantly under large eccentricities while the complex nonlinear relationship is depicted between these coefficients and large disturbances.
液体火箭发动机涡轮泵通常采用环形密封来控制流体介质的泄漏,以提高涡轮泵的工作效率[1-2]。然而密封在减小泄漏量的同时,还会产生流体激振力。该激振力一方面可引入一定的刚度阻尼,提高转子系统的临界转速,控制转子振动响应,甚至可取代轴承作为支承[3]; 另一方面,其引入的交叉刚度对转子系统稳定性构成威胁。
对于密封转子动力特性的研究,早期普遍采用基于整体流动理论(Bulk-Flow Theory)的求解方法,其忽略了密封径向速度变化情况,通过试验结果建立了壁面剪切力与平均流速之间的关系,极大地简化了求解过程[4]。该方法因其求解速度快,一定条件下可获得较为可靠的结果,在工程上得到了广泛的应用[5-10]。但由于整体流动模型是一种线性模型,只适用于小扰动情况,超出线性扰动范围之外将不再适用。因此,随着计算流体力学(CFD)技术的发展,利用三维CFD求解密封流场受到关注。相比传统Bulk-Flow模型,CFD方法无需做过多假设,理论上是更为精确的求解方法,并且可用于研究转子大扰动下的密封动力特性。密封的CFD求解方法主要有两种:CFD准稳态法和CFD瞬态法。CFD准稳态法最早由Tam等[11]提出,该方法假定转子绕密封中心轴线做圆形涡动,通过引入固定在转子上的动参考系,将瞬态问题转化为稳态问题,从而避免了瞬态模拟的复杂耗时,是近年来在密封动力学研究中使用最为广泛的求解方法[12-18]; CFD瞬态方法则直接在静止坐标系下对密封流场进行模拟,对密封结构及涡动轨迹等无限制,是研究密封的一种普适方法。但由于瞬态方法复杂耗时,并且在处理小间隙网格变形等方面存在诸多难点,因此在工程应用方面受到限制,目前的研究还集中在提高瞬态求解效率对结构较为复杂的阻尼密封开展相关研究[19-22]。
对于实际工作的涡轮泵小间隙密封,由于安装精度以及转子弯曲等原因,通常会在偏心状态下运行; 此外,涡轮泵内复杂流动引起的激振现象往往会使转子扰动超出线性小扰动范围,基于线性小扰动的密封动特性计算方法不再适用。然而目前对于涡轮泵转子大偏心尤其是大扰动下密封动力学特性的研究还比较匮乏。
本文分别采用修正的Bulk-Flow模型和CFD准稳态法对我国某型液体火箭发动机涡轮泵浮动环密封在大偏心以及大扰动下的动力学特性进行了研究。并且通过试验数据对两种方法的求解精度及可靠性进行了验证。
涡轮泵密封两端通常承受较高的压差,由于介质粘度较小,导致其内部流动表现为高度的湍流流动。图1给出了密封几何结构及相应坐标系。
基于整体流动理论,建立密封内的流体控制方程组[23-24]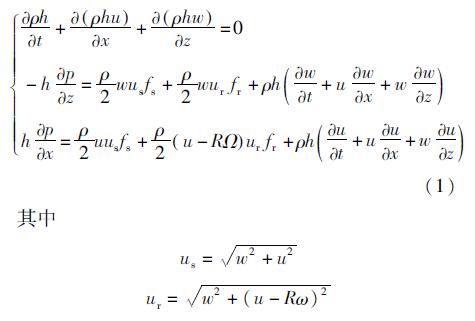
fs=0.001 375*[1+(104*(rs)/h+(106)/(Res))]1/γ,Res=ρhus/μ
fr=0.001 375*[1+(104*(rr)/h+(106)/(Rer))]1/γ,Rer=ρhur/μ
h=Cr(1+ecos(x/R))
式中:ρ为介质密度; h为密封间隙; u为密封周向平均速度; w为轴向平均速度; p为流体压力; us,ur分别为静子、转子表面速度; fs,fr分别为静子、转子表面阻力系数; γ为壁面摩擦系数; t为时间; R为转子半径; Ω为转子表面角速度; Cr为密封半径间隙; e为偏心率。
在获得密封流场控制方程组后,基于线性摄动理论获得零阶以及一阶摄动方程组,具体过程详见文献[25]。求解零阶摄动方程组,并对密封出口轴向平均速度进行积分获得密封的泄漏量
Q=∫2π0whdθ(2)
求解一阶摄动方程组,对密封间隙流域压力进行积分,基于最小二乘法线性拟合,即可获得密封刚度、阻尼以及惯性系数
Kαβ-ω2Mαβ=-∫L0∫2π0ΓαpβνRdθdz
ωCαβ=-∫L0∫2π0ΓαpαζRdθdz(3)
式中:ω为涡动转速; K为刚度系数; C为阻尼系数; M为惯性系数; α, β=X, Y; ΓX=cosθ,ΓY=sin θ; 当β=X时,ν=a,ζ=b; 当β=Y时, ν=b, ζ=a。
本文采取文献[26]提出的有限元方法对摄动方程进行求解,并对模型中几个关键参数(如入口损失系数、预旋系数、湍流摩擦系数等)进行修正,以提高模型预测的准确性。
当转子在绕静偏心做小位移扰动时,密封流体激励力可用下式表示

式中:Fx,Fy分别为密封x,y方向的流体激励力; Kxx,Kyy为主刚度系数; Kxy,Kyx为交叉刚度系数; Cxx,Cyy为主阻尼系数; Cxy,Cyx为交叉阻尼系数; Mxx,Myy为主惯性系数。
当转子进行同心涡动时,密封动力特性系数中直接项相等,交叉项互为负值,此时,上式可转换为
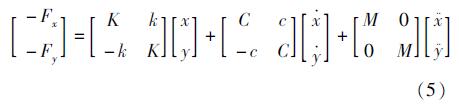
对于CFD准稳态法,其假设转子做同心圆形涡动,因此在转子中心建立转速等于涡动转速的旋转坐标系,即可将复杂的瞬态问题转换为稳态问题。此时作用在转子上流体径向力及切向力分别为
(Fr)/e=-K-cω+Mω2
(Ft)/e=k-Cω(6)
基于CFD仿真获得不同涡动转速下的Fr和Ft,代入式(6)进行拟合即可获得相应的密封动特性系数。
本文对两种密封模型进行仿真。模型一为试验条件下的密封结构用于对两种求解方法进行验证,其几何尺寸及运行参数如表1所示; 模型二为某型火箭发动机涡轮泵浮动环密封,其几何结构及受力情况如图2所示,密封半径间隙为0.15 mm,进出口压力分别为pin=23 MPa,pout=5 MPa; 转子转速为18 000 rpm。
为考虑密封预旋效应以及入口节流降压过程,对模型一入口远场流域以及模型二密封入口前泄漏流域也进行了建模。采用ANSYS Workbench对两种模型进行三维结构化网格划分,并对间隙壁面区域进行网格加密,两种模型的网格划分结果如图3~图4所示。采用了7套网格方案对两种模型进行网格无关性验证,间隙内网格层数分别为4, 6, 8, 10, 12, 14, 16层,模型一对应网格数在15*104~200*104之间,模型二网格数在52*104~86*105之间。网格无关性计算结果表明当网格层数超过8层时,泄漏量结果基本稳定,变化率不超过0.2%; 而密封流体激励力在网格层数超过12层时才逐渐稳定。因此为了保证仿真结果的可靠性,选择间隙网格层数为14层的网格方案进行研究,相应的模型一网格数为1 505*103,模型二网格数为5 604*103。
采取ANSYS CFX对密封流场进行仿真,对于密封动特性的研究使用较多的湍流模型为标准k-ε模型或其改进模型,近年来SST k-ω模型的应用逐渐增多[14-15],均获得了较好的计算结果。本文对标准k-ε,RNG k-ε以及SST k-ω三种模型仿真结果与试验进行对比,最终确定选取SST k-ω模型进行后续仿真研究。利用本文数值方法与文献[27]中基于Fluent软件,Reliazable k-ε模型的三种仿真方法获得的结果进行对比如表2所示。可以看出,本文基于CFX软件、SST k-ω的准稳态方法与文献中的两种准稳态方法相比,获得的结果更佳,其计算精度与瞬态方法精度一致。其中主刚度系数误差较大,文中给出的原因是主刚度系数对密封上游状态敏感性较大,而模型中未考虑上游状态的影响。
边界条件的选取:模型一根据试验测量结果给定入口静压以及出口静压边界条件; 模型二为了更好考虑叶轮旋转引起的预旋效应,根据文献[28]中涡轮氧泵全流场仿真结果给定速度入口以及压力出口边界条件。转子壁面角速度设为(Ω-ω),密封壁面角速度设为-ω。收敛残差为1*10-7,同时监控流量曲线以及流体激励力作为收敛判定准则,当所有结果稳定后即认为计算结果达到收敛。最后选取5种涡动频率比ω/Ω = -1,-0.5,0,0.5,1计算密封动力学特性系数及泄漏量。
密封动力学特性试验在哈尔滨工业大学的高转速间隙密封试验台[29]上进行。利用所获得的试验数据对修正的Bulk-Flow模型以及CFD准稳态法计算结果进行验证。
在Bulk-Flow模型求解中,利用CFD仿真结果对入口损失系数以及预旋系数进行修正; 通过试验结果并基于泄漏量相等的原则,对湍流摩擦系数进行修正。修正后的入口损失系数及预旋系数分别为0.5和0.22,湍流摩擦系数为3。仿真与试验结果对比如表3所示。
由表3可以看出,两种方法均能较好地预测密封动力特性系数,其中CFD方法具有更高的求解精度。修正的Bulk-Flow模型对密封各动特性系数的预测均偏高,其中主刚度系数预测误差为10.32%,交叉刚度误差为13.65%,主阻尼误差为26.84%,交叉阻尼误差为43.04%; CFD方法对主刚度系数预测偏低,而对其他系数预测偏高,其中主刚度与交叉刚度预测误差仅为4.07%和3.47%,主阻尼误差为19.63%,交叉阻尼误差为44.30%。在泄漏量预测上,由于修正的Bulk-Flow模型是基于与试验泄漏量相等原则来修正湍流摩擦系数,因此与试验结果保持一致; 此外,CFD准稳态法能够准确预测泄漏量,与试验结果非常接近。因此后续研究可通过CFD求解泄漏量结果对湍流摩擦系数进行修正。
值得一提的是,本文试验以及仿真获得的交叉刚度显著大于主刚度系数。对于低压差浮动环密封,文献[30]结果表明,当锁定偏心率<0.35时,密封交叉刚度系数Kxy,Kyx均大于主刚度系数Kxx,Kyy,其中负交叉刚度系数Kyx远大于主刚度系数Kxx,Kyy。而本文试验台密封锁定于同心位置,因此出现交叉刚度大于主刚度这种情况。
涡轮泵浮动环密封在稳定运行时一般会处于锁定状态,其锁定位置由于重力等影响往往会处于偏心位置。此外,由于浮动环密封间隙相对更小,在涡轮泵内流体复杂激励作用下转子扰动往往会超出线性扰动范围,传统线性化方法预测的动特性系数将不再适用。因此,本章利用修正的Bulk-Flow模型对转子偏心状态下密封动特性进行研究,并通过CFD方法对转子大扰动下密封所表现的非线性动力学特性进行研究。
假设浮动环锁定位置与转子同心,基于小扰动理论对密封动特性系数进行求解。在利用Bulk-Flow模型求解时,基于CFD仿真结果对模型经验参数进行修正,修正后的入口损失系数为0.58,预旋系数为0.4,湍流摩擦系数为3.5。
表4分别给出了利用Bulk-Flow以及CFD方法获得的浮动环密封动特性系数。可以看出,两种方法获得的密封动特性系数十分接近,这一定程度上也证明了仿真求解的可靠性。对于高压高转速涡轮泵,采用小间隙浮动环密封引入的主刚度系数达到1*108 N/m以上,与滚动轴承的支承刚度量级相当,因此在涡轮泵转子动力学特性的研究中,密封影响不应忽略。此外,对于采用刚性转子低温氧泵来说,轴承阻尼较小可忽略,密封作为唯一可引入较大阻尼的部件,其主阻尼系数达到40 kN·s/m以上,通过合理的密封设计,可能会对涡轮泵转子系统振动的抑制起到良好的效果。
图5给出CFD仿真获得浮动环密封轴向截面压力分布。可以看出,密封入口处由于流道截面迅速减小,流速增大,压力迅速降低(见局部放大图),导致一部分能量损失。密封间隙内部压力随着密封长度增加逐渐减小,在出口处达到最低值,符合密封的实际工作状态。
实际运行过程中,密封通常会处于不同程度的静偏心状态。大偏心下,其对密封动力学影响将不可忽视。利用修正的Bulk-Flow模型对浮动环在静偏心率0~0.8范围下的动力学特性进行研究。图6给出密封刚度系数随静偏心率的变化曲线。可以看出,当偏心率小于0.2时,刚度系数基本保持不变; 当偏心率大于0.2时,刚度系数随偏心率增加而增大,大偏心下增大幅度加快; 主刚度系数Kxx较Kyy增加幅度更大,偏心率0.8时,Kxx增加了56.94%; 交叉刚度kyx较kxy增加幅度更大,偏心率0.8时,kyx增加110.8%。
图7给出密封阻尼系数随静偏心率的变化曲线。同样在静偏心率小于0.2时,阻尼系数变化较小; 而当偏心率大于0.2时,阻尼系数随静偏心率的增大显著变化。其中主阻尼系数Cxx,Cyy均随静偏心率增大,且Cxx增加幅度更大,偏心率0.8时,增加了85.57%; 而交叉阻尼系数cxy,cyx却呈现不同的变化规律:cxy随偏心率增大逐渐减小,偏心率0.8时减小48.90%; 而cyx则随偏心率增加而增大,且在大偏心时增大幅度迅速增加,当偏心率为0.8时,Cyx增大了190.29%; 因此总的来说,密封的交叉阻尼随着转子静偏心的增加体现出增大的趋势。 图8给出惯性系数及泄漏量随静偏心率的变化曲线。同样在静偏心率小于0.2时,惯性系数及泄漏量基本保持不变; 随着静偏心率的增大,泄漏量缓慢增加,而惯性系数则显著增加。其中Mxx增大幅度更大,当偏心率为0.8时,Mxx增加了102.37%。但总体上由于浮动环长度较短,其引入的惯性系数并不是很大。在线性密封动力学研究中,基于小扰动理论,转子的扰动半径控制在0.1Cr以内,以满足线性假设,来获取密封动特性系数。而对于高压高转速涡轮泵,流体诱发的结构振动剧烈,加之浮动环密封间隙较小,因此转子扰动将超出线性范围,处于大扰动状态。本节利用CFD方法对不同扰动偏心(偏心率范围0.05~0.8)下密封间隙内流场进行仿真,利用式(5)和式(6)拟合获得大扰动下密封的等效动特性系数。仿真过程中,假设浮动环锁定位置与转子同心。
图9给出刚度系数对扰动偏心率的变化曲线。可以看出,主刚度及交叉刚度系数均随扰动偏心的增加呈现出复杂的非线性关系。在小偏心扰动下刚度系数保持一致,表明传统线性化动力学系数假定的合理性。当扰动偏心增加时,主刚度系数首先迅速下降,在偏心率0.3时达到最低值,此后随着偏心率继续增加,主刚度系数一致处于增大趋势; 交叉刚度随偏心率增加先缓慢下降,在偏心率大于0.3后开始增大,且在大扰动下增大趋势迅速增加。可见大扰动下密封引入的交叉刚度会对转子系统的稳定性构成威胁。
图 10给出了阻尼系数随扰动偏心率的变化曲线。同样不同扰动偏心下阻尼系数呈现出复杂的非线性关系,且在小扰动下,阻尼系数基本保持不变。随着扰动的增大,主阻尼呈现出先降低后增大的趋势,当扰动偏心率为0.3时,主阻尼系数达到最低; 而交叉阻尼随扰动偏心的增加呈现出先增大后迅速降低的趋势,当扰动偏心率为0.4时,交叉阻尼达到最大值。 图 11给出不同扰动偏心率下密封惯性系数及泄漏量曲线。可以看出,扰动偏心对泄漏量没有影响,但却对惯性系数影响较为复杂。随着扰动偏心的增加,惯性系数先降低,在偏心率0.3时达到最低,而后开始增大,在偏心率0.4时达到最大,最后又随着扰动量的增大迅速减小。 总的来说,转子在大扰动下,密封动特性系数呈现出复杂的非线性关系。对于采用浮动环密封的涡轮泵,在其转子系统振动特性的研究中密封与转子振动位移之间的非线性耦合作用不应被忽视。本文采用修正的Bulk-Flow模型以及CFD准稳态法对转子大偏心以及大扰动下的涡轮泵浮动环密封的动力学特性进行了研究,得出结论如下:
1)本文采用的修正的Bulk-Flow模型及CFD准稳态法均能较好地预测密封动特性系数,且CFD法具有更高地求解精度。其中Bulk-Flow模型对各动特性系数的预测均偏高,而CFD法对主刚度系数的预测偏低,其余系数的预测均偏高。
2)对于高压高转速涡轮泵,浮动环密封引入的主刚度系数达到108 N/m量级,与滚动轴承支承刚度量级相当,因此在涡轮泵转子系统动力学研究中,浮动环密封的作用不应被忽略。
3)转子静偏心量在一定程度上改变了密封动力学特性。总体来说,随着静偏心量增大,密封动力学系数均呈现出增大的趋势,且越大偏心下增大的趋势越快。
4)转子大扰动对密封动力学特性影响显著。不同扰动偏心下,密封各动特性系数呈现出复杂的非线性关系。在涡轮泵转子系统振动特性研究中,应当考虑密封的非线性耦合作用。