基金项目:国家自然科学基金(11602186)
作者简介:李小明(1966—),男,研究员,研究领域为航天推进技术
(1.西安航天动力研究所,陕西 西安 710100; 2.液体火箭发动机技术重点实验室,陕西 西安 710100; 3.航天推进技术研究院,陕西 西安 710100)
(1.Xi'an Aerospace Propulsion Institute, Xi'an 710100, China; 2.Science and Technology on Liquid Rocket Engine Laboratory, Xi'an 710100, China; 3.Academy of Aerospace Propulsion Technology, Xi'an 710100, China)
cartridge; shock wave; numerical computation; second-generation wavelet; artificial viscosity; similitude law
为了获得电爆管输出压力及其冲击波传播规律,针对电爆管爆炸燃气建立了一维流动模型,并采用自适应二代小波配点法进行数值计算。分析了电爆管冲击波沿一维等截面和局部变截面通道的传播过程及规律。结果 表明:自适应小波配点法结合人工黏性技术可以准确计算电爆管强冲击波传播问题; 电爆管爆炸冲击波沿一维等截面传火通道传播满足一定相似律,建立的相似律表达式能够估算同一类电爆管冲击波在爆炸近区的传播规律; 传火通道结构形式和结构参数变化对传播规律影响显著,针对同一类型的电爆管和变截面传火通道建立的相似律表达式,在1
In order to obtain the output pressure of cartridge and the propagation law of its shock wave, a one-dimensional flow model of the explosion gas was established, and the adaptive second-generation wavelet collocation method was applied in the numerical simulation.The propagation law of the shock wave along the one-dimensional equal section channel and the local variable section channel were analyzed. The results show that the adaptive wavelet collocation method combined with the artificial viscosity can precisely calculate the strong shock wave dashing out from the cartridge into the passage.The blast shock wave of the cartridge along the one-dimensional equal-section passage meets a certain similitude law, and the proposed similitude law formulas can estimate the propagation characteristics of the shock wave near the explosion field.The structural type and parameter of the passage have a significant effect on the propagation law.The similitude law expressions for the same type of cartridges and variable-section passage are proposed, and the estimated error is less than 10% under the condition of 1
电爆管是电爆阀、拔销器等装置的驱动能量源,具有能量密度高、体积小和工作可靠等优点。电爆管起爆后产生高温高压燃气,在传火通道中形成强烈冲击波,冲击波沿传火通道传播和驱动做功的同时,伴随着接触间断、稀疏波的传播、反射及其相互作用等复杂过程[1-2]。电爆管的压力输出特性决定着电爆阀、拔销器等装置的工作特性和可靠性。但是,由于爆腔和传火通道十分狭小,压力和温度极高,很难通过试验准确获取传火通道中压力分布和变化规律。目前利用容积数倍于真实爆腔的标准密闭爆发器测试电爆管的压力曲线,并利用峰值压力通过静态等温过程换算真实容腔的压力和驱动力[3]。由于忽略了冲击波传播的动态过程和空间分布特性,估算误差可能较大,而且不能评估传火通道结构对冲击波传播规律的影响。因此建立考虑空间分布的一维模型,分析电爆管冲击波传播过程和传播规律。
传统的冲击波计算方法如ENO,WENO,MUSCL及AUSM等为了获得高分辨率、高精度解,需要非常细密的网格,以便能捕捉清晰的冲击波结构。但是,精度和分辨率越高,计算量越大,特别是高维问题,除非使用非规则网格,否则因计算量巨大的原因将很难实现[4]。小波数值方法是基于多分辨分析(MultiResolution Analysis, MRA)发展的新方法,由于小波函数具有紧支撑特性,因此能够对流场数据进行压缩,生成捕捉流场局部结构的适应性网格,适合描述局部流动特征显著的问题[4-6],但仍处于发展阶段,并未广泛应用。
小波数值方法主要有两类,即小波-迦辽金和小波配点法[5]。小波-迦辽金法不适合处理非线性算子和任意边界条件,而自适应小波配点法在这两方面均具有优势,特别是二代小波,在真实物理域中进行变换,可以方便处理任意边界条件,因此发展迅速。文献[6]利用二代小波,采用自适应配点法计算了Burgers方程和含化学反应的无黏Euler方程; 文献[7]利用小波配点方法模拟了地震波在各向异性介质中的传播; 文献[8-14]研究了小波数值方法在激波、湍流、燃烧、爆轰波、水击等方面的应用。研究表明,小波数值方法在捕捉水击波、激波波、爆轰波以及火焰局部结构等方面具有显著优势,分辨率和精度高,计算量小。
本文基于一维Euler方程,采用自适应小波配点法(Adaptive Wavelet Collocation Methods,AWCM)对电爆管冲击波的传播过程进行数值计算。详细介绍自适应二代小波配点方法的原理、冲击波捕捉方法、计算过程,初步分析电爆管冲击波沿传火通道的传播规律。
根据多分辨分析理论可知,任意函数f(x)∈L2(R)的多尺度分解可近似为
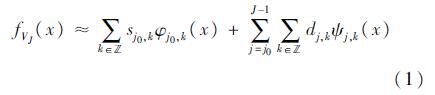
式中:sj0和φj0分别为尺度系数和尺度函数; dj和ψj分别为小波系数和小波函数; J为尺度因子。
第一代小波定义在整个实数域(-∞,+∞),处理实际问题时会产生边界效应,也不方便处理任意边界条件。二代小波不仅直接定义在物理域,而且为分解过程提供了更快速的算法。本文选用基于提升格式构造的二代小波,即提升插值小波。预测和更新均使用左右各2个点,即N=N~=2,预测算子P和更新算子U分别为
P={-1/(16),9/(16),9/(16),-1/(16)}
U={-1/(32),9/(32),9/(32),-1/(32)}(2)
分解过程分为3步:分裂(Split)、预测(Predict)和更新(Update),如图1所示。
分裂:按尺度因子J进行规则采样S={ck,k=0,…,2J},然后将S按顺序号奇偶分为Se和So两部分。预测:利用偶序列中相邻的2N个点预测奇序列,设P为预测算子,则有
dj-ik=cj2k+1-∑Nl=-(N-1)pj-1k,lcj2k+2l(3)
更新:为了使原信号集的局部特性在子集中保持,利用相邻的2N~个点进行更新,设U为更新算子,则有
cj-ik=cj2k+∑l=-(N~-1)uj-1k,ldj-1k+l(4)
逆变换过程为
cj2k=cj-ik-∑l=-(N~-1)uj-1k,ldj-1k+l(5)
cj2k+1=dj-ik+∑Nl=-(N-1)pj-1k,lcj2k+2l(6)
对于局部包含小尺度特征的函数,仅在相应的局部位置小波系数较大,而大部分小波系数将会很小,即便舍去这些系数很小的小波函数,也能很好地逼近原函数。基于这种思想,人工选定或通过某种规则计算得到一个阈值ε(ε>0),根据小波系数相对于阈值的大小分为两部分

由于每个小波函数(也包括尺度函数)和配点一一对应,因此舍去小波的同时删除了对应的配点,从而生成自适应网格。对于正则方程,舍去式(9)中系数较小的小波,逼近的误差上限为[6]
‖f(x)-f≥(x)‖≥C1ε‖f(x)‖(10)
添加人工黏性项的一维Euler方程
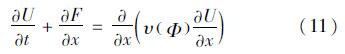
式中:U为守恒变量; F为通量。等号右侧为人工黏性项,人工黏性υ为冲击波定位函数Φ(或称通量限制器)的函数,而Φ随小波系数的大小变化。最细尺度的小波系数能反应冲击波位置,而对于j
Φk=min((|djmaxk|)/(‖u‖),1)(12)
Euler方程组包含多个守恒变量,理论上需要对每个变量进行小波变换,并分别计算冲击波定位函数。考虑到冲击波问题和一般黎曼问题的共性,选择守恒变量ρ进行小波变换、生成适应性网格以及构造冲击波定位函数,有利于简化计算和节约计算量。但对于强冲击波问题,可能会由于人工黏性不足,并不能有效抑制数值振荡。考虑到Φ在[0,1]区间内变化,采用幂函数形式的定位函数能够控制黏性分布的宽度
Φk=min(((|djmaxk|)/(‖u‖))α,1)(13)
对于强冲击波问题,一般指数因子α<1,以便有效抑制数值振荡。利用冲击波定位函数控制的人工粘性[4]
υ=1/2Φ(c+|u|)Δx(14)
式中:c为当地声速,c=(γp/ρ)1/2; u为速度。
通量的空间导数采用二阶中心差分格式,守恒量的时间导数采用一阶步进格式,则方程(11)的离散格式为
(Un+1-Un)/(Δt)=-(Fni+1-Fni-1)/(2Δx)+
1/2(|vi+1/2|(Ui+1-Ui)/(Δx)-|vi+1/2|(Ui-Ui-1)/(Δx))(15)
具体步骤为:
1)由t时刻的值通过二代小波变换获得各尺度的小波系数;
2)根据小波系数相对于阈值ε的大小删除相应的小波函数,从而生成自适应网格;
3)在自适应网格上计算空间导数;
4)选择时间步长Δt,计算(t+Δt)时刻的值,并返回1)继续计算。
这种算法可以适当调整网格,尺度因子越大,则分辨率越高; 选择的阈值越小,精度越高。
电爆管一般属于标准火工品元件,匹配不同的阀门或者拔销器的结构,可能在连接部位形成变截面的传火通道。根据不同的匹配形式,将电爆管传火通道简化为4类一维流道,作为不同结构型面的近似,即等截面、锥形扩张、锥形收缩以及拉瓦尔喷管型结构。局部截面积线性增大或减小,截面变化的过渡距离与爆腔长度相同,因此变截面特征可以仅通过一个参数——截面面积比
η=A/(A0)(16)
式中:A0为爆腔横截面积,当为拉瓦尔喷管结构时,传火通道与爆腔横截面积相同; A为喉部截面积,当为锥形结构时,A为扩张或收缩后的传火通道截面积; η<1为收缩型; η>1为扩张型。如图2所示,截面变化的过渡距离与爆腔长度L均为10 mm。特别地,η=1为理想的等截面模型,对于变截面通道,定义Δη=|1-η|,用于表征相对于等截面通道的变化程度。
假设炸药在电爆管爆腔内瞬时完成定容反应,并完全达到化学平衡,初始条件如图3所示,根据爆炸腔的容积,炸药及其大量爆炸产生物的性质计算初始参数如表1所示。状态方程采用理想气体状态方程,燃气比热比γ=1.25。电爆管封闭端设为刚性壁面条件,出口可使用压力出口或压力远场条件,在冲击波到达出口前,均不影响上游冲击波的计算。为了验证计算方法在强冲击波条件下的准确性,利用可求得精确解的冲击波管问题进行验证,计算域为[-5,5],初始条件与电爆管模型完全相同,即表1所示。基础网格点为1 025个(J=10),滤波阈值ε=2*10-5。图4所示为5 μs和10 μs时刻速度分布,可以看出自适应小波配点法(AWCM)的计算结果与黎曼解符合得很好,并且无明显的数值振荡,表明冲击波的小波捕捉方法能够准确计算强冲击波问题,适用于电爆管冲击波传播特性的预测。采用自适应算法,删除了变化平缓区域的大量网格点,使网格点主要集中在冲击波波阵面、稀疏波以及接触间断区域。
取爆腔长度L=10 mm、传火通道长度l=10 L,电爆管冲击波传播过程的计算参数与冲击波管相同。计算的冲击波传播速度为3.62 km/s,经过约27.6 μs传播至传火通道的右端出口,与黎曼解完全一致,表明计算准确。图5为传火通道中不同位置的压力历程和不同时刻压力分布,可以看出,爆腔内压力衰减迅速,10 μs时,爆腔内最大压力衰减为200 MPa,20 μs时,最大压力约为40 MPa; 压力随传播距离迅速衰减,距离爆腔越近,峰值压力衰减率越大,如图6所示。
对于等截面的传火通道,不同位置的峰值压力p与爆腔长度L、初始压力p0和传播距离x有关,构建无量纲的传播距离x/L和峰值压力pm/p0,分两个区间拟合指数形式的无量纲函数,结果如式(17)所示,其中x/L>1时的函数曲线如图6所示。对于同一类电爆管,爆炸冲击波传播相似律如下(pm)/(p0)={exp(-1.74(x/L)0.18),0.1 exp(-2(x/L)0.25),1.0
在相同的初始条件(表1)下,计算局部变截面传火通道压力在0~25 μs内的发展变化,结果如图7所示,其中η=1表示等截面传火通道,作为不同结构比较的基准。
对于拉瓦尔喷管型结构,喉部面积减小导致输出压力降低,且对爆炸近区的影响更显著,η=0.75时,x/L=1和2处的峰值压力分别降低18%和9%。而对于纯收缩或扩张型结构,传火通道截面积越小,输出压力越高,在x/L=2的位置,η=0.75和0.5时,峰值压力对应增大27%和78%,而面积增加25%和50%时,峰值压力相应减小15%和28%。可以看出,在相同的初始条件下,变截面传火通道内不同位置的峰值压力不仅取决于传播距离x,而且受传火通道结构形式和参数η的影响,传播规律更为复杂。构建无量纲的峰值压力pm/p0、传播距离x/L以及局部截面面积比η,利用数值计算的结果拟合得到不同位置无量纲的峰值压力pm/p0与传播距离x/L和局部截面积比η之间的关系如下
(pm)/(p0)=3.1η1.63exp((-0.96lnη-2.82)(x/L)1/4)(18)
(pm)/(p0)=386exp(-4.96η1/2+(1.22η-3.99)(x/L)1/4)(19)
利用3.2节中假设的电爆管模型(p0=187.68 MPa,L=5 mm)进行验证,不同位置峰值压力和估算误差如表3和表4所示。当1
基于二代小波配点法和人工黏性技术,构造了冲击波的小波数值计算方法,并应用于电爆管一维冲击波数值计算,根据计算结果初步分析了电爆管爆炸冲击波的传播规律,分析表明:
1)自适应小波配点法结合人工黏性技术可以准确计算电爆管强冲击波传播问题。
2)电爆管爆炸冲击波沿一维等截面传火通道传播满足一定相似律,建立的相似律表达式能够准确估算同一类电爆管冲击波在爆炸近区的峰值压力。
3)传火通道结构形式和参数变化对冲击波传播规律影响显著,针对同一类型的电爆管和传火通道建立的相似律表达式在1