根据发动机部件的特点建立各部件的静态特性方程,然后根据发动机的系统组成对发动机各流路建立压力平衡、流量平衡和功率平衡的关系式,最终建立如下的发动机系统非线性模型

F_i(D,X)=0, i=1,2,…,n(1)

式中:D(d₁,d₂,…,d_n)为关注的目标参数; X(x₁,x₂,…,x_n)为发动机推力和混合比,为包含随机信息的发动机各部件参数。

求解非线性方程组可以使用数值方法,其中拟牛顿法因其具有计算量小和收敛速度快的特点而被广泛使用。该方法设(x^(k)₁,x^(k)₂,…,x^(k)_n)是方程组的一组近似值,围绕这组近似解可以再构造n组近似解; 第j组近似解(x^(k_j)₁,x^(k_j)₂,…,x^(k_j)_n)(j=1,2,…,n)与(x^(k)₁,x^(k)₂,…,x^(k)_n)除第j个分量相差一个常数h>0外,其余均相同,即

{x^(k_j)_i=x^(k)_i+h, i=j

x^(k_j)_i=x^(k)_i, i≠j(2)

其中

Δx^(k)_i=x_i-x^(k)_i,(i=1,2,…,n)

当系数行列式不等于零时,上述方程组有唯一解。于是由上式得到的解为

x^(k+1)_i=x^(k)_i+Δx^(k)_i,(i=1,2,…,n)(5)

当迭代得到差值小于设定值时,计算收敛。

单因素敏感性分析即研究发动机性能与某一个影响因素的相关性。

若发动机某项性能参数F_i会受到m个因素的影响,分别记为a₁,a₂,a₃,…,a_m,则可以根据发动机静态特性方程建立数学模型

F_i=f(a₁,a₂,a₃,…,a_m)(i=1,2,…,n)(6)

把发动机设计状态作为基准状态,此时影响因素空间为{a^*₁,a^*₂,…,a^*_m},对应发动机性能参数空间为{F^*₁,F^*₂,…,F^*_n}。当某个影响因素a_j(j=1,2,…,m)在一定范围内发生变化,即当影响因素空间变为{a^*₁,a^*₂,…a'_j,a^*_m}时,发动机性能参数空间随之变化为{F'₁,F'₂,…,F'_n}。记影响因素的偏差量为Δa_j=a'_j-a^*_j,发动机性能参数F_i的偏差量为ΔF_i=F'_i-F^*_i,则定义发动机性能参数相对偏差与对应影响因素相对偏差之间的比例关系为发动机性能参数对该影响因素的敏感性,记作

S(a_j)=(|ΔF_i|/F^*_i)/(|Δa_j|/a^*_j)(7)

可以看出,敏感性越高,发动机性能参数随影响因素变化的变化幅度就越大,即影响因素对发动机性能的影响越明显。单因素敏感性分析方法简单,能够快速直观地反映发动机性能随某一影响因素变化的变化梯度。但是单因素分析方法每次只能对影响因素空间的某一点进行分析,通过对某一方向的局部梯度判断影响因素的作用效果,存在一定的片面性^[4]。

单因素敏感性分析操作简单,结果直观,但只能就单一因素变化时发动机性能受到的影响进行研究,无法准确分析多因素共同作用对发动机性能产生的影响。液体火箭发动机结构复杂,部件的非线性和参数的耦合性都很强,在工作时往往会有很多参数偏离设计值,使发动机性能受到多个参数变化的共同作用。在这种情况下,单因素敏感性分析就不能满足需求了,需要进行多因素敏感性分析。

同样将设计状态作为分析的基准状态,改变影响因素空间中k个元素的值,将其变为{a'₁,…,a'_k,a^*_k+1,…,a^*_m},通过计算可以得到对应的发动机性能参数空间{F'₁,F'₂,…,F'_n}。如果使用排列组合找出影响因素所有可能的组合方式,就可以计算出对应各种影响因素空间的发动机性能参数映射,得到在所有可能情况下影响因素对发动机性能的影响。但是,影响发动机性能的参数较多,这样做会带来巨大的工作量。如分析9个影响因素,每个影响因素水平数为3,则包含每个因素不同水平的组合共有3⁹=19 683种,要依次进行分析是难以实现的。因此,多因素敏感性分析常采用正交试验法设计不同的影响因素组合^[11]。

正交试验法即从所有的排列组合中选取部分有特点、有代表性的子样,使各影响因素、各因素水平的分布具有均匀散布和整齐可比的特点,即各个因素的每个不同水平在试验中出现的次数均相同; 任意两个因素所有不同水平的搭配均在试验中出现,且出现的次数都相同。这样就可以通过部分试验得到与全部试验同等可信的结果,极大减少试验的次数。一般使用正交表来安排正交试验^[12]。

在以前的研究中,常采用极差分析法对试验结果进行统计和研究。

假设多因素敏感性分析的试验结果为y_I(i=1,2,…,n),将第j个因素同水平的结果加起来,记作X_k=(k=1,2,…,l),表示第j个因素中水平为k的结果之和。若每种因素水平为k的试验有z次,则将该因素水平为k的平均结果记作x_k=X_k/z,计算该因素所有水平的平均结果的极差R_j=max(x_k)-min(x_k),就可以反映该因素对目标参数的影响程度。极差越大,说明该因素水平变化对目标参数的影响越大。

极差法原理简单,计算速度快,结果直观易懂,但是只能分析出不同因素对目标参数影响程度的相对大小,无法判断每个因素对目标参数影响程度的显著性,而且也不能区分影响因素水平变化引起的目标参数变化和试验误差引起的目标参数变化。要排除试验误差带来的影响,并分析出不同因素对目标参数影响程度的显著性,就需要使用方差分析法^[13-17]。

若使用正交表L_n(q^m)进行正交试验,将第k号试验结果记为y_k,k=1,2,…,n。并记

T=∑ⁿ_k=1y_k,y^-=T/n,r=n/q(8)

S_T=∑ⁿ_k=1(y_k-y^-)²(9)

S_j=r∑^q_i=1((T_ij)/r-y^-)²=1/r∑^q_i=1T²_ij-(T²)/n,j=1,2,…,m(10)

式中:y^-为所有试验结果的算术平均数; r为某个影响因素同一水平的重复次数; S_T称为总体的离差平方和,表征所有试验结果的离散程度; T_ij表示第j个因素水平为i的所有试验结果之和; S_j称为第j列的离差平方和,表征第j个因素不同水平试验结果的离散程度。在正交试验中,有

S_T=∑^m_j=1S_j(11)

将二次型S_T的秩称为S_T的自由度,记作f_T; 同理定义S_j的自由度,记为f_j。则有

f_T=n-1(12)

f_j=q-1,j=1,2,…,m(13)

f_T=∑^m_j=1f_j(14)

若正交表中有未安排影响因素的空列,则该列的离差平方和作为误差平方和,记作S_e,它的自由度记作f_e。

如果试验的结果相互独立,且服从等方差为σ²的正态分布,那么S₁,S₂,S_m互相独立。如果在某一列j中,T_1j,T_2j,…,T_qj相互独立,且同样服从方差为σ²的正态分布,则认为该列因素对试验结果的影响不显著,则有

S_j/σ²～x²(f_j),j=1,2,…,m(15)

选取统计量

F_j=(S_j/f_j)/(S_e/f_e)(16)

如果影响因素的作用不显著,则有

F_j～F(f_j,f_e),j=1,2,…,m(17)

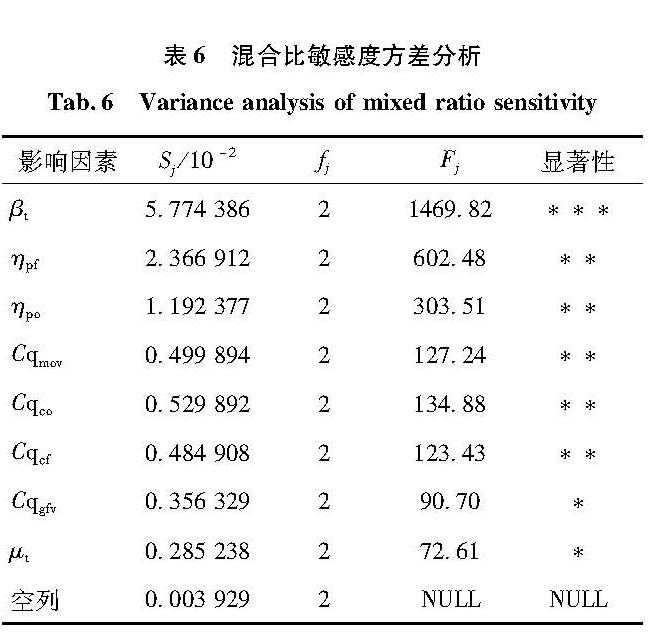
给定显著性水平α,可以通过查F分布表可以得到F_j(f_j,f_e)的值,然后由公式F_1-α(f_j,f_e)=1/F_α(f_j,f_e)求出F_1-α(f_j,f_e)的值,如果F_j>F_1-α(f_j,f_e),则认为该因素的影响显著,反之则认为影响不显著。当判断因素的影响显著时,显著性水平α越小,则认为影响的显著性越高。

在进行方差分析时,可以首先求出每一列的平均离差平方和,即

S^-_j=S_j/f_j (18)

对于第j列,如果S^-_j-_e,就将S_j看做误差平方和,并入S_e中,同时也将该列的f_j并入到f_e中。记并入后的误差平方和为S^*_e,对应的自由度为f^*_e。此时选取的统计量变为

F^*_j=^△(S_j/f_j)/(S^*_e/f^*_e)(19)

当F^*_j>F_1-α(f_j,f^*_e)时,则认为在置信度为1-α的情况下,因素j对试验结果的影响显著,反之则认为影响不显著。

可以看出,方差分析能够有效地把影响因素的离散程度和与误差的离散程度区分开,并通过F检验法分析出每个因素对试验结果影响的显著性大小,进而找出对试验结果造成影响的主要因素。与极差法相比,方差分析法更准确、更可信,分析得出的信息量也更大。

某型在研65 t级液氧/甲烷发动机采用燃气发生器循环,同轴涡轮泵布局,发动机系统如图1 所示。在地面级发动机中,推力F_e和混合比r_e是设计人员最关心的性能参数,因此选取推力和混合比作为研究的目标参数。

图1 液氧/甲烷发动机系统示意图
Fig.1 Schematic diagram of liquid oxygen/methane engine system

能够对发动机性能产生影响的干扰因素分为内部和外部干扰因素。外部干扰因素是由发动机工质和外部环境带来的干扰,可以精确测量并采取措施加以控制,一般认为是非随机变量; 内部干扰因素则是由发动机本身带来的干扰,即在制造过程中,因加工误差,零件安装差异以及部件液流试验测量误差等造成发动机部件特性具有一定的随机散布性,一般认为是随机变量^[2]。

在这些随机变量中,有两类对发动机工况的影响最直接,即流路的流阻特性和部件的性能参数。这两类参数也恰好最容易受到加工误差和工艺稳定性的影响,是需要重点关注的。此外,边界条件也会影响发动机的工作状态,是需要关注的。因此,我们从外部边界条件、流路的流阻特性和涡轮泵的性能特性中选出19个比较有代表性的参数^[18-19],分别为甲烷泵入口压力(p_ipf)、氧泵入口压力(p_ipo)、甲烷主管路流阻系数(Cq_pmf)、氧主管路流阻系数(Cq_pmo)、甲烷副管路流阻系数(Cq_psf)、氧副管路流阻系数(Cq_pso)、推力室甲烷喷嘴压降(Cq_cf)、推力室氧喷嘴压降(Cq_co)、发生器甲烷喷嘴压降(Cq_gf)、发生器氧喷嘴压降(Cq_go)、涡轮喷嘴流量系数(μ_t)、涡轮效率系数(β_t)、甲烷泵效率系数(η_pf)、氧泵效率系数(η_po)、甲烷主阀流阻系数(Cq_mfv)、氧主阀流阻系数(Cq_mov)、甲烷副阀流阻系数(Cq_gfv)、氧副阀流阻系数(Cq_gov)、燃气管路流阻系数(Cq_pg)。

选取影响因素后,需要确定影响因素的水平数。因素的水平数是指该因素取值的个数。一般情况下,选择两水平数进行分析,得到对目标参数的影响一般是线性的,选择三水平数或者更多的水平数,得到的结果一般呈二次曲线,甚至是更高次曲线,可以更好地趋近真实的情况。因此,选择三水平数或更多的水平数,能够提高分析的准确性。本文从仿真准确性和计算规模两个方面综合考虑,在单因素敏感性分析中,每个因素均选择五水平数,即基准值和分别偏离基准值-20%,-10%,10%,20%; 在多因素敏感性分析中,每个因素均选择三水平数,即基准值和分别偏离基准值-10%,10%。

使用2.1节中介绍的原理,对选出的19个参数进行单因素敏感性分析,得到发动机推力敏感度如表1所示; 发动机混合比敏感度如表2所示; 推力和混合比对不同影响因素的平均敏感度直方图如图2所示,其中,横坐标1～19代表的影响因素分别为甲烷泵入口压力(p_ipf)、氧泵入口压力(p_ipo)、甲烷主管路流阻系数(Cq_pmf)、氧主管路流阻系数(Cq_pmo)、甲烷副管路流阻系数(Cq_psf)、氧副管路流阻系数(Cq_pso)、推力室甲烷喷嘴压降(Cq_cf)、推力室氧喷嘴压降(Cq_co)、发生器甲烷喷嘴压降(Cq_gf)、发生器氧喷嘴压降(Cq_go)、涡轮喷嘴流量系数(μ_t)、涡轮效率系数(β_t)、甲烷泵效率系数(η_pf)、氧泵效率系数(η_po)、甲烷主阀流阻系数(Cq_mfv)、氧主阀流阻系数(Cq_mov)、甲烷副阀流阻系数(Cq_gfv)、氧副阀流阻系数(Cq_gov)、燃气管路流阻系数(Cq_pg)。

图2 平均敏感度直方图
Fig.2 Average sensitivity histogram

表1 发动机推力敏感度
Tab.1 Thrust sensitivity of engine

表2 发动机混合比敏感度
Tab.2 Mixing ratio sensitivity of engines

虽然对发动机推力和混合比影响最大的3个因素是相同的,但是有一些因素对推力和混合比的影响差别较大。例如副系统氧阀流阻系数Cq_gov,对推力的影响程度排在第4位,敏感度为0.132 3,对混合比的影响则排在第10位,敏感度仅为0.058 1,二者相差2.3倍; 又如推力室氧喷嘴流阻系数Cq_co,对推力的影响程度排在第10位,敏感度仅为0.039 8,但对混合比的影响程度却排在第5位,敏感度为0.164 0,二者相差4.1倍。

根据单因素敏感性分析,发现部分因素对发动机推力和混合比的影响非常小,为减小不必要的工作量,提高计算效率,可以在进行多因素敏感性分析的时候将其忽略。通过分析,从19个因素中分别选出对推力和混合比影响较为明显的因素进行多因素敏感性分析。

由于发动机静态特性方程组的非线性很强^[20],因此当多因素同时变化时,求解方程组的难度会增大,甚至可能出现计算不收敛的情况。为了保证方程收敛并提高计算效率,仅选取3个水平进行仿真。根据选择的因素数和水平数,选择L₂₇(3¹³)正交表设计仿真试验。发动机推力敏感性试验的组合方式及试验结果如表3所示,发动机混合比敏感性试验的组合方式与试验结果如表4所示。

表3 推力敏感度试验及结果
Tab.3 Thrust sensitivity test and results

表4 混合比敏感度试验及结果
Tab.4 Mixed ratio sensitivity tests and results

使用方差分析法对正交试验结果进行分析。结果如表5和表6所示,已知F_0.95(2,2)=19,F_0.99(2,2)=99,F_0.999(2,2)=999,对比得到各因素的影响显著性,其中*的数量越多,表示影响越显著。

由表5和表6分析可以看出:

1)传统的极差分析法只能得到各因素对性能参数影响程度的相对大小,而方差分析法可以获得各因素对发动机性能影响的显著性大小,结果直观,与极差分析法相比,既能够提高发动机性能敏感性的分析准确度,又可以加深设计人员对各因素实际影响程度大小的认识。

2)对于发动机推力和混合比,涡轮效率对性能的影响均高度显著,即涡轮效率与发动机性能参数有着极强的相关性,涡轮效率的改变会引起发动机性能参数较大范围的改变。

3)甲烷泵效率和氧泵效率对发动机推力的影响均为高度显著,对发动机混合比的影响较显著,但其显著性明显高于其他影响较显著的因素。通过查表得F_0.995(2,2)=199,即当选择的显著性水平α=0.005时,甲烷泵效率和氧泵效率对发动机混合比的影响显著性比其他因素要高出一个等级。

综上,涡轮泵的效率对发动机性能有着十分显著的影响,其影响程度远大于其他因素,因此在设计与加工过程中,对涡轮泵的关键几何参数要提高精度要求,降低加工散差,同时还需要通过涡轮气流试验和泵水力试验或通过实际热试车获取涡轮泵的实际效率,并以此为基础,使用调节元件对发动机进行参数调节,以保证发动机性能参数满足总体要求。

表5 推力敏感度方差分析
Tab.5 Variance analysis of thrust sensitivity

表6 混合比敏感度方差分析
Tab.6 Variance analysis of mixed ratio sensitivity