基金项目:国家自然科学基金(11475131)
作者简介:杨振宇(1994—),男,硕士,研究领域为空间电推进技术
(西安航天动力研究所 陕西省等离子体物理与应用技术重点实验室,陕西 西安 710100)
(Shanxi Key Laboratory of Plasma Physics and Applied Technology, Xi'an Aerospace Propulsion Institute, Xi'an 710100, China)
RF ion thruster; inductively coupled plasma; numerical calculation model; performance analysis; electric propulsion
射频离子推力器是空间电推进的一种,其推力性能是系统设计的核心问题。为获得推力特性随设计参数的变化规律,采用数值计算方法进行了研究,开展了1 mN射频离子推力器设计计算,对不同放电室尺寸、流量、射频功率、屏栅电压下的推力性能进行了分析并进行了工况优化。结果 表明,模型能够正确地描述射频离子推力器性能变化规律,放电室内径25 mm的推力器即可以实现1 mN推力指标,在最优工况下,推力器推力1.176 mN,比冲2 503 s,效率53.13%,满足设计要求。根据该模型研制的推力器样机成功点火,验证了数值模型的有效性,可以利用该模型为射频离子推力器研制工作提供指导。
RF ion thruster(RIT)is a kind of electric propulsion, and the thrust performance is the core issuse of propulsion system design. Numerical calculation method was used to obtain the thrust characteristic with design parameters. The design of a 1 mN RIT was carried out, thrust performance of different discharge chambers, mass flowrates, rf power and screen voltage were analyzed and the working condition was optimized. The results show that the model can correctly describe the performance variation law of RIT, and thrust of the RIT with a discharge chamber of 25 mm inner diameter can reach 1 mN. Under the optimal working condition, thrust 1.176 mN, specific impulse 2 503 s and efficiency 53.13% can be achieved, which meets the design requirements. The thruster prototype developed according to the model was ignited successfully, which fully verified the effectiveness of the numerical model, the numerical model can be used to guide further research.
随着深空探测、星际航行及卫星组网等新兴空间技术不断发展,研制质量轻、体积小和效率高的推进系统已经成为航天推进技术发展的重点。电推力器具有高比冲、长寿命、推力精确可调等优点,在各项航天任务中得到长足的发展。
目前国际上得到广泛应用的空间电推进技术主要有霍尔电推进与离子电推进两类。美国XR-5,俄罗斯SPT-140,欧洲PPS5000等霍尔推力器已在飞行器平台上得到应用[1-2]; 美国XIPS-25、英国T-5等离子推力器也在姿态控制、轨道转移、深空探测等航天任务中得到广泛应用[3-4]。
射频离子推力器是通过感性耦合放电产生等离子体并通过离子光学系统引出离子束的电推力器,主要技术特点为:无电极放电,无外加磁场,束流均匀,可实现参数宽范围调节。与霍尔推力器与离子推力器相比,射频离子推力器除了具有长寿命、高比冲、推力连续精确可调等特点之外,还具有结构简单、易于开展扩比和缩比设计等优点,非常适用于地球同步轨道卫星位置保持和轨道转移、深空探测主推进、航天器姿态控制等任务,同时也可满足微纳卫星姿态与轨道控制、编队飞行和无拖曳控制等任务需求[5-7]。德国最早提出并开展射频离子推力器研究,RIT-10 成功将ARTEMIS卫星送入地球同步轨道,之后又研制了RIT-2.5,RIT-4,RIT-15,RIT-22,RIT-35 等覆盖微小功率和中高功率范围的射频离子推力器。
当前国内外学者主要在理论分析、数值模拟及试验研究3个方面对射频离子推力器开展工作,其中,理论分析和数值模拟主要着眼于放电过程建模分析及束流引出机制,放电过程研究重点在于通过放电机理分析、射频功率耦合计算优化参数设计,实现推力器稳态放电[8-11]; 束流引出机制研究聚焦于栅极参数对引出电流的影响规律,通过优化栅极设计提升推力器性能[12-13]; 试验研究重点在功率耦合测试,得到推力器点火功率[14-16]; 在较为成熟的推力器上进行推力测试试验来优化推力器推力性能[17-19]。目前射频离子推力器推力性能研究主要以试验手段为主,需针对特定型号搭建地面测试平台,获得推力性能变化规律,研制成本较高,研制周期长,普适性较差,因此开展推力性能数值计算研究,在短周期内获得不同参数下的推力性能参数,可在研制初期提供理论指导,具有重要的学术及工程应用价值。
本文基于对射频离子推力器内部物理过程的分析建立了推力器性能数值计算模型,与现有的计算模型相比,在0维放电模型与变压器模型上增加了束流引出模型,通过数值计算即可以得到放电参数也可以直接获得推力器推力、比冲、效率等推力性能参数。利用该模型对1 mN级射频离子推力器进行了设计计算,分析了放电室尺寸、流量、射频功率、栅极电压等关键参数对推力器性能的影响规律,基于模型设计的结构参数研制了射频离子推力器地面样机,推力器成功点火,说明该模型的有效性,可用于指导下一步研制工作。
射频离子推力器结构如图1所示,性能计算模型用于分析氙工质射频离子推力器稳定放电时推力器的性能参数,下标e,i,n分别为电子、离子、中性气体,假设:
1)电子、离子、中性粒子处于热平衡,即麦克斯韦分布;
2)电子密度取平均密度ne,电子温度取平均温度Te;
3)放电室内部满足准中性条件,即ne≈ni,离子与中性粒子处于壁温下的热平衡,Ti=Tn=Tw;
4)电离只发生在等离子体内部,电子离子只在器壁上复合,考虑等离子体损失时,忽略栅极开孔。
利用整体ICP放电模型计算放电参数,首先根据电子温度及壁面温度即求出中性气体密度。然后建立放电粒子平衡方程。
离子以玻姆速度uB进入鞘层,则等离子体损失率为
n·e|lost=2πR2innehLuB+2πRinLnehRuB(1)
其中
hL=0.86[3+l/(λi)+((0.86luB)/(πγDi))2]-1/2
hR=0.8[4+R/(λi)+((0.8RuB)/(Ji(2.405)γDi))2]-1/2
式中:Rin为放电室内径; L为放电室长度; hL,hR分别为放电室上下底面、圆柱面鞘层边缘处密度与中心密度比值[20]; λi为离子平均自由程; γ为电子温度与离子温度的比值; Di为离子扩散系数,对于氙来说,离子与中性粒子平均碰撞截面
Q-in=8.280 72×10-16/ci
式中:ci为麦克斯韦分布平均热速度。对于射频离子推力器,放电室内电子平均温度在5 eV左右,并没有达到氙的第一级电离能(12.1 eV),所以电离碰撞截面可以线性表示为
σion(E)=σ0(E/(eVi)-1)(2)
σ0取3.63×10-20m2,则等离子体生成率可表示为
n·e=πR2inLnennσ0ce(1+2(kBTe)/(eVi))exp(-(eVi)/(Te))(3)
式中:Vi为氙原子第一级电离能。联立式(1)和式(3)即可得到放电室中粒子平衡方程
nnσ0ce(1+2(kBTe)/(eVi))exp(-(eVi)/(Te))=uB(2RinhL+2LhR)/(RinL)(4)
给定放电室气压、壁面温度,该方程仅与电子温度有关,求解该方程可以得到电子温度。粒子平衡方程中并没有给出电子密度,需要考虑能量平衡方程来确定电子密度,放电室中能量平衡方程为
(Pabs)/(πR2inL)=neυen(3me)/(mn)kB(Te-Tn)+(n·e)/(πR2inL)(1+(eVexc〈σc〉exc)/(eVi〈σc〉i))eVi(5)
式中Pabs为等离子体吸收的射频能量。右端第一项代表弹性碰撞的能量损失,第二项代表用于电离与激发的能量,尖括号项表示麦克斯韦激发系数与电离系数的比值,由电子温度确定。求解能量平衡方程即可确定电子密度。
射频离子推力器放电属于ICP放电,采用变压器模型计算等离子体吸收功率,变压器模型中需要计算趋肤深度
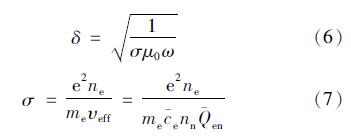
式中:σ为等离子体电导率; υeff为有效弹性碰撞频率; c-e为电子平均热运动速率,根据电子温度计算得出。
传感器模型等效电路如图2所示,Rc与Lc分别是射频天线阻抗与感抗,R2与L2分别是等离子体阻抗与天线互感组成的阻抗和感抗
R2=-(ω2L2mRp)/(R2p+(ωLp)2)(8)
L2=-(ω2L2mLp)/(R2p+(ωLp)2)(9)
式中:Rp为等离子体阻抗; Lp为等离子体感抗,忽略等离子体惯性感抗; Lm为线圈互感。
将等离子体阻抗耦合进初级电路后,即可计算电流Ic,Ic支路阻抗为Z1=(Rc+R2)+iω(Lc+L2)(10)
并联电容支路阻抗为
Z2=RESR-i1/(ωC)(11)
RESR为等效串联阻抗,则电路总阻抗为
Z=(Z1Z2)/(Z1+Z2)(12)
VS为初级电路电压,则等离子体吸收功率为
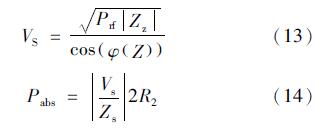
求出等离子体吸收功率后即可代入功率平衡方程计算电子密度。
射频离子推力器中电离度往往较低,所以不能用经典Child-Langmuir理论中空间电流限制计算栅极引出电流,采用改进的Child-Langmuir理论计算引出电流,如图3所示。
定义有效长度le=βls+ts+lg(15)
式中:ls为屏栅表面鞘层宽度; β为比例系数; ts为屏栅厚度; lg为屏栅和加速栅的间距。则引出电流表示为

式中:Vtotal为屏栅电压与加速栅电压之和; da为加速栅孔径; Nholes为开孔数目。获得引出电流Jbeam,即可得到推力器出口离子数流量Γi,屏栅与加速栅的几何透明度分别为φs,φa,栅极面积为As,则栅极引出中性粒子数流量为
Γn=(nnc-n)/4As1/(1/(φs)+1/(φa)-1)(17)
然后可以根据Γn与Γi计算出气体利用率ηn,进而得出推力器入口工质流量。由于入口工质速度较低,计算推力时忽略放电室入口动量,推力
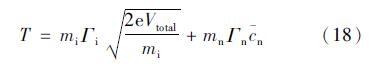
式中c-n为中性粒子热运动平均速率。
图4为放电过程计算框图,在确定放电室、栅极结构参数后,输入流量、壁温、射频功率、频率、屏栅电压、加速栅电压,首先给定初始气压、电离率与电子温度,计算出中性粒子密度后,采用牛顿法迭代求解粒子平衡方程(6)更新电子温度,收敛后用变压器模型计算等离子体吸收功率,进而求解能量平衡方程(7)更新电子密度、电离度、流量,直到流量收敛于输入流量,计算结束,使用束流引出模型计算推力性能。
1 mN射频离子推力器设计指标如表1所示。假设推力器输入功率50 W,推进效率为50%,则产生1 mN推力,比冲大约为2 500 s,推进功率为25 W,考虑到推力器还有中和器、贮供单元、测控单元需要额外供电,预设射频功率为10 W进行计算,屏栅与加速栅电压分别预设为1 500 V,-150 V。
参考国内外现有射频离子推力器结构尺寸,放电室内径在20~30 mm左右即可产生约1 mN的推力,预设放电室长度为20 mm,保持其他参数不变,对内径20,25,30 mm放电室进行计算,流量预设为0.5~1.0 sccm。计算结果如图5所示,可以看到,不改变其他条件,流量在0.5~1.0 sccm范围内,推力器推力随流量增大而增大,比冲随流量增大而减小,这是因为推力器的推力由引出离子流量和离子速度决定,在射频功率不变的条件下,等离子体吸收的功率基本不变,而由于增加流量中性粒子密度增加,虽然电离的中性粒子总数增加,但电离度减少,又因为栅极电压不变,对离子的加速作用不变,所以引出离子流量增大导致推力增大,推进剂利用率减小,比冲降低。同时可以看到,在20,25,30 mm 3个尺寸中,20 mm内径放电室达不到推力1 mN的指标,25 mm内径放电室推力即可以达到1 mN,不需要继续增加放电室尺寸,所以放电室尺寸定为25 mm。
放电室内径确定后,需要分析放电室长度对推力器性能的影响,进而获得放电室长度,流量0.6 sccm,射频功率10 W,屏栅电压1 500 V,加速栅电压-150 V,放电室长度15~25 mm,计算结果见图6。由计算结果可以看到,在给定输入条件下,增加放电室长度,推力、比冲单调下降,这是由于等离子体主要在放电室器壁上损失,其他条件不变,增加放电室长度会增加等离子体损失面积,进而降低引出离子流量,所以推力比冲下降。同时可以看出,放电室长度在15~25 mm推力都可以达到1 mN,但是推力器不宜过短,否则气流在放电室驻留时间过短不易点火,考虑到这一因素,将放电室长度确定为24 mm。
图5 不同放电室内径、不同流量下的推力、比冲
Fig.5 Thrust and specific impulse of different discharge chamber inner diameters and different flowrates
射频离子推力器工作时,射频功率、流量、栅极电压等工作参数都会对推力性能产生影响。在功率、结构的限制下,应详细分析推力、比冲、效率随各参数的变化规律,找出推力器工作的最佳工况。计算时,直流电源的效率取0.9,射频电源的效率取0.8,中和器等其他部分功率约为5 W,总功率不超过50 W。
首先分析射频功率对推力器工作性能的影响,流量0.6 sccm,屏栅电压1 500 V,加速栅电压-150 V,射频功率10~20 W,计算结果如图7所示,图中显示推力、比冲随射频功率增大而增大,且总功率增加,但是效率降低。
图8为不同射频功率的电离度及电子密度。射频功率主要用于电离中性气体和加热等离子体,射频功率由10 W增加到20 W后,等离子体密度由9.68×1017 m-3增加到1.96×1018m-3,所以引出离子流量增加,推力比冲上升,然而射频功率增高电子温度上升,将会有较大一部分射频功率用于加热等离子体而不是电离,所以效率降低。在射频功率为14 W时,总功率已增加到50 W,所以在屏栅电压1 500 V时,注入射频功率不应超过14 W,为留有一定余量,注入射频功率定为12 W。 栅极起到聚焦、引出离子的作用,屏栅电压起主要作用,流量0.6 sccm,射频功率12 W,加速栅电压-150 V,屏栅电压1 400~1 700 V,计算结果如图9所示。 可以看到栅极电压上升,推力、比冲、功率与效率都呈上升趋势,这是因为增大栅极电压可以增强对离子的加速作用,单位流量的离子可以产生更大推力,所以推力、比冲效率都会上升,离子速度上升,引出电流增加,进而功率增加。但屏栅电压不宜过高,否则引起功耗过大、击穿放电和栅极离子溅蚀等问题,屏栅电压定为1 600 V。最终将推力器的工作条件设置为:流量0.5 sccm,射频功率2 MHz,射频功率12 W,屏栅电压1 600 V,加速栅电压-150 V,射频离子推力器推力性能参数见表2,放电室等离子体参数见表3。
基于对射频离子推力器内部物理过程的分析建立了推力器性能数值计算模型,主要包括0维放电模型、变压器吸收模型、束流引出模型,通过该模型对1 mN射频离子推力器进行了设计计算,分析了放电室尺寸、流量、射频功率、栅极电压等关键参数对推力器性能的影响规律,可以得到以下结论:
1)射频离子推力器推力与比冲随放电室内径增大而增大,推力随流量增大而增大,比冲随流量增大而减小; 推力器放电室内径25 mm,推力即可达到1 mN,放电室长度增大会使等离子体损耗增加,推力性能下降。
2)增大射频功率,推力器推力、比冲、效率均会增大,但是会增加总功耗。
3)栅极电压对推力器性能起到非常重要的作用,增加屏栅电压,性能改善明显,但同时也会增加功耗并引起击穿放电和离子溅蚀等问题。
4)根据该模型研制的射频离子推力器样机成功点火,验证了该模型的有效性,可为下一步研究工作提供指导。