1.1 基于串联刚度模型的轴向力估算方法
转子轴系在转子端部的主要结构示意图如图1所示,其中主轴承为三点角接触球轴承。当转子受到图1所示向左的轴向力时,轴向力F的力传递路径如图中箭头所指路线,即转子组件所产生的轴向力F首先压向轴承内圈,内圈通过轴承滚珠传递至轴承外圈,外圈通过压紧螺母传递至轴向力传感器,最终传递至壳体。此时轴向力传感器受到压缩载荷作用。当转子轴向力向右时,力的传递路径反向,轴向力传感器受到拉伸作用。
某液体火箭发动机的泵水力试验中,轴向位移传感器实测轴端位移向左0.306 mm(不含轴承轴向游隙),说明轴系轴向力向左,轴向力传感器受压缩载荷作用(如图1所示)。此时轴端位移X主要由轴向力传感器轴向压缩变形、轴承滚动体与滚道之间挤压变形引起的内外圈轴向相对位移、轴承压紧螺母的轴向变形、轴向力传感器压紧盖板的轴向变形等几部分组成。这几部分可等效为串联弹簧模型,各部分轴向位移大小主要由其轴向刚度决定,刚度越小产生的位移越大。
1—壳体; 2—轴向力传感器; 3—轴; 4—转子组件;
5—轴承; 6—轴端螺母; 7—位移传感器。
图1 转子轴系轴向力向左时的力传递路径示意图
Fig.1 Force transmitting path of the rotor shaft when the axial load faces toward left
当忽略轴向刚度较大的轴承压紧螺母和轴向力传感器压紧盖板等零部件的轴向变形时(这些零部件轴向刚度比轴向力传感器刚度和轴承刚度至少大一个数量级),则轴向位移主要由轴向力传感器和轴承引起,如图2所示,则简化的弹簧串联刚度模型中,其位移和力的关系如下
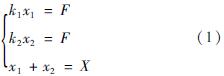
式中:k1为轴向力传感器的轴向刚度; x1为轴向力传感器的轴向位移; k2为轴承的轴向刚度; x2为轴承的内圈和外圈轴向相对位移; F为轴向力大小; X为转子轴端位移传感器测量值,即总位移大小。
图2 转子轴向位移简化示意图
Fig.2 Simplified schematic diagram of rotor axial displacement
式(1)中,总位移大小X已知,由轴端位移传感器测出,若刚度k1和k2可以得到,则式(1)方程组中的3个未知数x1、x2和F均可求出,即可得到轴系的轴向力大小。因此求解轴向力问题转化为求解轴向力传感器和轴承轴向刚度的问题。
1.2 轴系刚度计算
1.2.1 轴向力传感器轴向刚度
轴向力传感器结构与典型的鼠笼式弹性支承结构类似,但本文所涉及的轴向力传感器并不承受径向载荷,也不用来调整临界转速或降低整机振动,而仅仅用于测量轴向力的大小,且拉压载荷均能进行测量。轴向力传感器轴向刚度可以采用材料力学分析方法得出近似的计算公式,但仅限于在方案设计阶段粗略估算其刚度范围。对于具体结构的精确刚度计算,可采用有限元方法得到[16]。
对轴向力传感器进行有限元弹塑性分析,其材料为铝青铜QAl10—3—1.5,材料性能参数[17]为:弹性模量105 GPa,屈服极限210 MPa,强度极限650 MPa,断裂伸长率30%。针对本文所涉及的受载情况,仅计算其受压时的刚度。固定轴向力传感器左侧端面,在右端面施加向左的载荷,在1 000 N轴向压力下,轴向力传感器的轴向变形约0.81 μm,如图3所示,则轴向力传感器受压时线弹性阶段的轴向刚度为k1=1.23×109 N/m。
图3 轴向力传感器受压时的轴向变形
Fig.3 Axial deformation of axial force sensor under pressed
轴向力传感器在其弹性工作范围之内时,其轴向刚度基本保持不变,若轴向力过大,力传感器结构进入塑性阶段时,则其刚度将发生变化,甚至无法进行轴向力的测量。因此对轴向力传感器施加更大轴向力进行弹塑性有限元分析,得到端面轴向位移随着载荷的变化曲线如图4所示。由图可知,当载荷大于130 kN时,轴向力传感器位移会急剧增加,即结构发生塑性变形,无法进行正常测力。
图4 轴向力传感器的位移—载荷曲线
Fig.4 Displacement-loads curve of axial force sensor
1.2.2 轴承轴向刚度及试验
轴承轴向刚度可根据经验式(2)进行计算[18]

式中:Fa为轴向力; Z为轴承滚珠个数; d为轴承滚珠直径; β为轴承的接触角。该经验公式为单列向心球轴承的刚度近似计算公式,可用于本文的角接触球轴承刚度粗略估算[19]。当进行轴向力的精确计算时,轴承的轴向刚度对结果具有重要影响,因此对轴承开展轴向刚度试验。
轴承轴向刚度试验需要在转子旋转状态下施加轴向力,精确测量内外圈之间的相对位移变化,从而计算出轴承轴向动刚度。轴承动刚度随着转速的增加会发生刚度软化现象,预紧力越大,软化点越高[20]。本文轴承工作状态下承受较大的轴向力,转速对刚度软化的影响相对较弱,当忽略滚动体所产生的离心力和陀螺力矩的影响时,可近似采用轴承静刚度代替动刚度。考虑到旋转状态下的轴承动刚度试验较难实现,本文仅进行静态加载下的轴向刚度试验,测试时轴向力间隔2 kN分段逐级施加,最大施加至60 kN。
轴承轴向刚度试验结果如图5所示,同时与经验式(2)进行对比。从图5可知,轴承轴向刚度试验结果与经验公式(2)基本一致,轴向刚度随着轴向力的增加而增大,在轴向力为15~40 kN时,两曲线基本重合,误差较小。当轴向力小于15 kN时,经验式(2)的刚度计算结果比实际值偏大,而轴向力大于40 kN时,经验式(2)的刚度计算结果比实际值小。
图5 轴承轴向刚度实测值与经验公式结果对比
Fig.5 Comparison of measured axial stiffness of bearing with calculated results by empirical formula
1.3 轴系的轴向力计算
根据以上对轴向力传感器和轴承轴向刚度的分析可知,当轴向力小于130 kN时,轴向力传感器的轴向刚度恒定,约为1.23×109 N/m,而当轴向力大于130 kN时,轴向力传感器发生塑性变形,其轴向刚度将会发生变化; 而轴承轴向刚度随着轴向力的增加而增加。因此式(1)中的刚度k1和k2均为轴向力F的函数,采用式(1)进行轴向力求解时,需要采用迭代算法求解。
为简化计算过程,可将迭代求解轴向力F的复杂过程转化为图解法求解,将轴向力传感器和轴承两部分轴向位移—载荷关系曲线进行叠加,即可得到不同轴向力作用下的总位移。具体做法为:利用有限元弹塑性分析得到轴向力传感器位移—载荷曲线(见图4),再与轴承轴向刚度试验的实测位移—载荷数据进行叠加,即可得到总位移—载荷关系曲线,如图6所示。
图6 总位移—载荷关系曲线
Fig.6 Variation of total displacement with axial load
由
图6可知,在0~60 kN的轴向力范围内,轴系的轴向总位移主要由轴承产生,这是由于轴承轴向刚度远小于轴向力传感器轴向刚度,其产生的轴向位移相对较大。
泵水力试验时测得的轴端总位移为0.306 mm,由图6可以得到此时对应的轴向力为39.3 kN。