基金项目:国家自然科学基金(51606138)
作者简介:杨尚荣(1986—),男,博士,高级工程师,研究领域为液体火箭发动机喷雾燃烧。
(1.西安航天动力研究所 液体火箭发动机技术重点实验室, 陕西 西安 710100; 2.中国航天科工集团公司六院210所,陕西 西安 710065)
(1.Science and Technology on Liquid Rocket Engine Laboratory, Xi'an Aerospace Propulsion Institute, Xi'an 710100, China; 2. 210 Institute, The Sixth Academy of China Aerospace Science & Industry Corp., Xi'an 710065, China)
coaxial swirl injector; thermoacoustic instability; recurrence network; network measures; intermittency
为获得同轴离心式喷嘴燃烧动力学特性,开展了喷注单元稳定性试验研究。试验中随着混合比的增加,系统依次经历了燃烧噪声状态、阵发状态和准周期振荡状态。采用递归网络方法对实验结果进行分析,获得了典型工况下的网络拓扑图。燃烧噪声状态体现出随机特征,阵发状态体现出中央聚集和极限环边界特征,准周期振荡状态体现出宽边界圆环特征。利用网络全局测度对系统动力学状态转变过程进行量化估计,发现聚类系数、特征路径长度、介数中心性、网络直径、全局有效性、同配性等均可作为同轴离心式喷嘴燃烧动力学转变过程的表征指标。
An experimental investigation of a laboratory-scale coaxial swirl injector in a cylindrical combustor was carried out. The dynamic behavior transits from combustion noise to quasiperiodic oscillations via intermittency with increasing mixture ratio. The topologies of recurrence networks constructed from the time series of acoustic pressure for three typical equivalence ratios were obtained. It is founded that the topologies show characteristics of random, central concentration and limit cycle boundary, and torus in the state of combustion noise, intermittency and quasiperiodic oscillation respectively. Topological measures of complex networks, namely clustering coefficient, characteristic path length, betweenness centrality, global efficiency, network diameter and assortativity were computed and used to distinguish different dynamical regimes in a turbulent combustor. It is found that these network properties capture the change in physical state of the system dynamics during the transition from combustion noise to combustion instability.
热声系统中火焰、流场和声场间存在复杂的耦合关系,因此,热声系统可以作为复杂系统处理[1]。复杂网络方法常用来研究复杂系统[2],研究思路为首先将研究对象转换为网络结构形式(仅包含节点和边),然后利用网络测度(包括节点、边、全局测度)进行量化分析。近来被应用到热声系统的动力学研究中,可以获得更多非线性动力学特性方面的信息,此外,基于复杂网络方法,可以发展出热声系统中热声振荡和贫燃熄灭的预测方法[3]。
Murugesan利用可视化网络(visibility networks)方法将压力时间序列转变为复杂网络,发现燃烧噪声具有无标度(scale—free)网络特征[4],而热声不稳定具有规则的分布特征。王金华利用可视化网络构建了湍流火焰面的拓扑结构,标记出对湍流火焰面有较大影响的关键褶皱结构,分析了湍流与火焰的相互作用规律[5]。Okuno采用周期网络(cycle networks)和k—邻近网络(k—nearest neighbors)研究了燃气轮机模型燃烧器中的热声不稳定现象,发现热声不稳定具有准周期和高维度特征,节点度显示出幂律型分布,同时较小的平均路径长度和较大的聚类系数说明系统存在小世界(small—world)特征[6]。Gotoda利用改进的可视化网络和递归网络研究了湍流受限火焰的熄灭过程,发现接近火焰熄灭时的燃烧状态具有小世界特征,网络的平均度可以作为火焰熄灭的在线预测工具[7]。Murugesan在钝体稳焰湍流燃烧器的动力学研究中,发现复杂网络的一些测度,如特征路径长度、聚类系数、网络直径、全局有效性可作为热声振荡和贫燃熄灭的预测指标[8-9]。Godavarthi利用递归网络方法[10],发现特征路径长度、介数中心性可对湍流燃烧器中的动力学转变过程进行预测。Murayama利用旋涡间相互作用构造了湍流网络,研究了预混火焰燃烧噪声阶段速度场的动力学特征,发现其具有无标度网络特征[11]。
同轴离心式喷嘴是液体火箭发动机常用的双组元喷嘴之一,对其燃烧稳定性的研究一直受到学者们关注。Miller开展了同轴离心式喷嘴燃烧试验,发现对于特定喷嘴,燃烧不稳定只发生在一定的频率范围内[12]。Wierman研究了气中心同轴离心喷嘴的燃烧响应,发现氧喷嘴长度对振荡幅值的影响较大[13]。王枫研究了气液同轴喷注器的结构尺寸和工作参数对燃烧稳定性的影响,发现喷嘴缩进长度对燃烧稳定性裕量影响很大且存在相对最佳值[14]。王延涛试验发现气气同轴离心喷嘴的自发燃烧不稳定过程出现了“滞后”现象[15]。王迪开展了气液同轴离心式单喷嘴模型发动机燃烧试验,发现增加缩进长度会对纵向燃烧不稳定产生阻尼作用,但在某些特定的燃烧室长度下,上述阻尼作用可以忽略[16]。
本文开展同轴离心式喷嘴稳定性试验研究,采用递归网络方法分析同轴离心式喷嘴火焰动力学特性,为液体火箭发动机稳定性评估和预测提供参考。
燃烧试验系统原理如图1所示[15],系统用来进行单喷注器燃烧模拟实验研究[17]。
模拟燃烧室为敞口圆筒形结构,直径156 mm,高277 mm,垂直安放在模拟喷注器面板上。试验用喷嘴(见图2)[15]为带缩进室的同轴离心喷嘴,外喷嘴为离心煤油喷嘴,出口直径16.4 mm,内喷嘴为直流氧化剂喷嘴,出口直径13.4 mm,缩进室长度为10.5 mm。喷嘴安装于模拟燃烧室中间位置,出口与模拟喷注器面板平齐。氧化剂为400 ℃的富氧气(氧气88%+空气12%),燃料为410 ℃的煤油蒸气,均由换热器加热至相应温度。
递归网络是将时间序列转变为复杂网络的其中一种方法。对于压力时间序列{x(i):i=1,2,…,m},由时间延迟重构技术可以得到延迟向量[19]

式中:d为嵌入维数,通过虚假最邻近法[20]确定; τ为延迟时间,取采样间隔的整数倍,通过互信息法[20]确定。
将延迟向量作为递归网络中的节点,计算二进制递归矩阵R,如果 是
是 的邻近点,则矩阵元素Rij等于1,否则矩阵元素Rij等于0。数学上写为
的邻近点,则矩阵元素Rij等于1,否则矩阵元素Rij等于0。数学上写为

式中:Θ为Heaviside函数; ε称为递归阈值; N=m-(d-1)τ为重构相空间中向量的数量; 2条轨迹间的距离通过L2范数进行计算。
递归网络的邻近矩阵元素Aij利用递归矩阵元素Rij由下式计算得到[20]
Aij=Rij-δij
式中δij为Kronecker delta。当i=j时,δij=1; 当i≠j时,δij=0。
邻近Aij提供了节点和节点间边的信息,如果Aij=1,则节点i和j有边相连; 如果Aij=0,则节点i和j不相连。从定义可以看到,递归网络是无向、对称、无权重网络。
试验中燃料流量不变,随着氧化剂流量的增加(混合比增加),系统从燃烧噪声转变为热声不稳定状态。图3中列出了典型工况下(混合比0.81、2.97、4.32)的压力时间序列。可以看到,混合比0.81时系统振荡幅值很低,为燃烧噪声状态。混合比2.97时,系统出现大幅值压力振荡和小幅值压力振荡间隔出现的现象,称为阵发现象。混合比4.32时,系统出现了幅值较一致的高幅值压力振荡。
不同混合比下的压力均方根值如图4所示。在混合比为2.35时,模拟燃烧室出现了自激燃烧不稳定,混合比为2.97时,振荡幅值达到最大,继续增加混合比,振荡幅值有所下降。压力均方根值常被用来在线评估燃烧系统的稳定性。但由于燃烧不稳定的幅值在出现不稳定之前是未知的,因此将其作为不稳定预测的参数不合适。此外,即使压力均方根值较高,也有可能是噪声引起的[10]。因此需要其他可以评估和预测燃烧不稳定的参数。
采用交互信息法求最优延迟时间τ时,取互信息法的第一个局部最小值为最优延迟时间。求得混合比0.81、2.97、4.32时最优延迟时间τ分别为0.11、0.07、0.07 ms。图5显示了混合比2.97时最优延迟时间计算结果。
图7中列出了典型工况下(混合比0.81、2.97、4.32)的递归网络拓扑图。混合比0.81时为燃烧噪声状态,体现出随机网络特征。混合比2.97时为阵发状态,网络图显示出中央聚集和周期边界特点,中央聚集表示系统为低幅值振荡,由递归图分析可知[18],系统为准周期振荡,周期边界代表系统为大幅值极限环振荡状态。混合比4.32时为准周期振荡状态,显示出宽边界圆环特征。可以看出,递归网络拓扑图体现出了不同燃烧动力学状态下吸引子的几何特征。
采用递归网络中几种全局测度对系统状态转变过程进行量化估计。分别利用1 000( )、1 500(
)、1 500( )、2 000(
)、2 000( )个数据点计算各网络测度值,见图8。可以看出,除介数中心性(数值随数据点个数增加而向下平移减少,但表现出相同的变化规律)外,其他网络测度值均体现出了良好的收敛性。
)个数据点计算各网络测度值,见图8。可以看出,除介数中心性(数值随数据点个数增加而向下平移减少,但表现出相同的变化规律)外,其他网络测度值均体现出了良好的收敛性。
平均度:单个节点的度定义为

代表与节点v相连的节点的数量。平均度定义为

平均度正比于递归量化分析中的量化指标——递归率[21],递归率在文献[18]中进行了分析,因此本文不再对平均度进行分析。
聚类系数:聚类系数是节点聚集性的测量,量化任意节点领域内的节点是否互为相邻节点。单个节点的聚类系数定义为
Cv=(2Nv)/(kv(kv-1))
式中:Nv为与节点v相连的节点之间边的数量; kv(kv-1)/2表示与节点v相连的节点之间最大可能的边的数量。整个网络的平均聚类系数定义为

从图8(a)看到,聚类系数在阵发振荡时值最大,燃烧噪声时值最小。说明燃烧噪声阶段,节点间相互独立性较强,体现出随机特性。阵发振荡存在低幅值准周期振荡(中央聚集),准周期振荡状态存在宽边界圆环聚集,因此聚类系数较大。
特征路径长度:节点i和节点j之间的最短路径长度Li,j定义为连接两节点所需要的最少边数,对于不相连的节点,Li,j=0。特征路径长度L定义为所有点之间最小路径长度之和与所有节点之间可能的边的数量的比值

从图8(b)看到,L在阵发振荡时值最大,准周期振荡和燃烧噪声时较小。阵发振荡时,高幅值振荡节点和低幅值振荡节点间距离远,路径长,因此特征路径长度大。噪声状态网络总边数较少(可从网络图的密度看出,与递归阈值ε的取值方法有关),正规化后特征路径长度小。
网络直径:网络直径定义为特征路径长度的最大值
D=max(Li,j)
从图8(c)看到,网络直径趋势与特征路径长度稍有不同,燃烧噪声时较小,阵发振荡和准周期振荡时值较大,说明燃烧噪声时节点互联度高。
全局有效性:全局有效性E定义为

表征节点间互达的有效性。对于不相连的节点,Li,j= 。全局有效性是最短路径长度的倒数和,因此,如果特征路径长度小,则全局有效性高,意味着网络是高度互联的。从图8(d)看到,全局有效性与特征路径长度趋势相反,燃烧噪声时值最大,说明节点高度互联。
。全局有效性是最短路径长度的倒数和,因此,如果特征路径长度小,则全局有效性高,意味着网络是高度互联的。从图8(d)看到,全局有效性与特征路径长度趋势相反,燃烧噪声时值最大,说明节点高度互联。
介数中心性:单个节点的介数中心性定义为经过该节点的最短路径与所有最短路径的比值

式中:σi,j为节点i和j之间最短路径的数量; σi,j(v)为节点i和j之间最短路径且经过节点v的数量。介数中心性确定相空间中连接两个高密度区域的低密度区域。从图8(e)看到,介数中心性在阵发振荡时值最大,准周期振荡时较小,燃烧噪声时值最小。较高的介数中心性说明吸引子具有较高的局部破碎[20](fragmentation)。阵发状态相空间中高密度区域的分布不一致,因此介数中心性在阵发状态时数值较大。
同配性:定义为所有边两端节点的Pearson相关系数
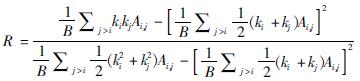
式中B=∑i<jAi,j为递归网络中边的总数。R取值范围为[-1,1],取正值时,说明节点均倾向于与自己度相当的节点相连,称为同配网络; 取负值时,说明度较高的节点倾向于与度较低的节点相连,反过来也一样,称为异配网络。
从图8(f)看到,同配性在3种状态下均为正值,即均为同配网络。在阵发振荡时值最大,准周期振荡时聚类系数较小,燃烧噪声时值最小。
通过上述计算分析,发现复杂网络的一些测度,如特征路径长度、聚类系数、介数中心性、网络直径、全局有效性等在3种燃烧状态下,其值存在明显的差异,因此均可作为同轴离心式喷嘴燃烧动力学转变过程的表征指标。进一步,与压力均方根值一起作为系统稳定性的判断标准,可以提高预警系统的可靠性。
采用递归网络方法对同轴离心式喷嘴燃烧稳定性进行了分析。获得了以下结果:
1)试验中随着混合比的增加,系统依次经历了燃烧噪声状态、阵发状态和准周期振荡状态。
2)网络拓扑递归网络体现出了不同状态下吸引子的几何特征。燃烧噪声状态显示出随机网络特征,阵发状态时显示出中央聚集和周期边界特点,准周期振荡状态显示出宽边界圆环特征。
3)网络测度,如聚类系数、特征路径长度、介数中心性、网络直径、全局有效性、同配性等均可作为同轴离心式喷嘴燃烧动力学转变过程的表征指标,可与压力均方根值一起作为系统稳定性的判断标准。