收稿日期:2020-05-31
基金项目:国家自然科学基金(51775412)
作者简介:何闯(1996—),男,硕士,研究领域为液体火箭发动机系统仿真。
基金项目:国家自然科学基金(51775412)
作者简介:何闯(1996—),男,硕士,研究领域为液体火箭发动机系统仿真。
Influence of gas drive pre-pressurized turbo-pump on frequency characteristics of liquid oxygen system in rocket engine
HE Chuang,XING Lixiang,XU Haohai
(Xi'an Aerospace Propulsion Institute, Xi'an 710100, China)
LOX/kerosene staged combustion cycle rocket engine; pre-pressurized turbo-pump; frequency characteristics; POGO; transmission matrix
备注
摘要
全文
图/表
参考文献
液氧/煤油补燃循环发动机液氧路频率特性对于火箭POGO振动和发动机动力学特性具有重要的意义。以某型液氧/煤油补燃循环发动机氧路流体系统为研究对象,重点考虑气涡轮和泵动态特性的影响建立了系统线性化小偏差频域模型。应用复系数状态空间矩阵法计算了气涡轮压比、氧预压泵动态增益、燃气掺混段特性对系统频率特性的影响。研究结果表明:预压涡轮低压比状态下,系统响应幅值变大,预压涡轮压比对系统频率影响较小; 预压泵动态增益越大,系统频率越低,幅值越大; 燃气掺混段长度越大,系统频率越低,幅值越小。
The frequency characteristics of liquid oxygen system in the LOX/kerosene staged combustion cycle engine are of great significance to the vibration of rocket POGO and the engine dynamics. Based on the liquid oxygen system in a LOX/kerosene staged combustion cycle engine,a linearized small deviation frequency domain model was established by emphatically considering the influence of gas turbine and pump dynamic characteristics.The influence of the gas turbine pressure ratio, the dynamic gain of the oxygen pre-pressurized pump and the gas mixing section on the system frequency characteristics were calculated by using the complex coefficient state space matrix. The results show that under the low-pressure ratio condition of the preloaded turbine, the system response amplitude becomes larger, which has less influence on the system frequency.The higher the dynamic gain of the pressurized pump, the lower the system frequency and the larger the amplitude.The longer the gas mixing section, the lower the system frequency and the smaller the amplitude.
引言
研究液体火箭发动机供应系统频率特性既是对发动机系统研究的关键步骤,又是进行运载火箭POGO振动分析和判别的必要工作。从20世纪60年代初开始,国外就对发动机供应系统展开了相关研究,Jesse l.Holster建立了发动机供应系统的频域传递矩阵模型[1]。G. Ordonneau采用有限元法对发动机的推进剂输送系统进行建模,并考虑了输送管路弯曲运动的影响[2]。近些年来,国内很多学者对发动机供应系统频率特性展开了相关研究[3-5]。我国的三三一工程POGO专题组对常规开式循环发动机的低频频率特性进行了全面的研究[6-10]。针对火箭POGO问题,国内许多专家也展开了发动机液氧路和蓄压器相关研究[11-13]。张黎辉等在低频区采用集中参数法,中频区采用分布参数法分析了某泵压式火箭发动机输送系统的频率特性[14]。邢理想等采用传递矩阵法分析了某型液氧/煤油补燃循环发动机的氧路低频动特性等[15-16]。张淼等在考虑泵间管路燃气射流冷凝的情况下分析了发动机氧路系统频率特性,验证了泵间管燃气射流冷凝过程是影响氧路系统频率特性的重要环节[17]。但是在以往的发动机氧路分析中,未考虑氧预压涡轮泵动态特性对于系统频率的影响。
某型液氧/煤油补燃循环发动机,采用高压燃气驱动氧预压涡轮,驱动后燃气掺混至泵后低温液氧,形成一段气液两相的流路,预压涡轮特性、泵特性和掺混段参数等因素都会导致发动机液氧路频率特性的变化。因此本文以该型发动机的液氧供应系统为研究对象,充分考虑氧预压涡轮泵特性参数的影响,建立各组件的线性化小偏差的传递矩阵模型,通过复系数状态空间矩阵法分析液氧路的频率特性和敏感参数的影响。
1 系统流路及数学模型
2 频率分析
3 结论
针对某型液氧/煤油补燃循环发动机液氧路建立了各组件线性小偏差频域模型,应用复系数状态空间矩阵分析了系统频率特性和敏感因素的影响,计算结果表明:
1)计算结果与试车符合较好,分析方法和模型可以应用于发动机系统频率特性分析。
2)在氧预压涡轮低压比小于设计点时,其影响氧路系统的幅频特性,使得系统幅值增大,降低了系统的稳定性。
3)氧预压泵动态增益越大,幅值增大,系统稳定性越差。
4)氧预压泵后的燃气掺混段是影响氧路系统频率特性的重要环节。燃气穿透长度增加,系统谐振频率减小,幅值减小; 燃气掺混段声速升高,系统谐振频率增大,幅值增大。
2.1 液氧路仿真与验证图3是某次高入口压力下氧预压涡轮泵转速和氧入口压力无量纲分频曲线,图4是仿真得到的试车台条件下发动机氧预压涡轮泵转速随发动机氧贮箱压力脉动的幅频曲线。
通过图3可以看出,发动机工作过程中,氧供应系统出现了约11 Hz的突频,在氧入口压力脉动、氧预压涡轮泵转速上具有明显体现。根据地面试车的供应系统状态,对氧系统进行仿真,考虑氧预压涡轮特性影响,系统二阶频率11.68 Hz,与试车时出现的突频相当,说明试车时的11 Hz突频为流体系统二阶频率。试车数据也验证了本文仿真方法的正确性。
图3 某次高入口压力试车氧预压涡轮泵转速和氧入口压力分频图
Fig.3 Frequency division diagram of oxygen pre—pressurized turbo pump speed and oxygen inlet pressure during a high pressure test
图4 液氧路仿真曲线
Fig.4 Simulation curve of liquid oxygen2.2 敏感性因素分析根据2.1节和工程实践,预压涡轮特性、泵特性和掺混段参数等因素都会导致发动机液氧路频率特性变化,本节对其敏感因素进行仿真分析。
2.2.1 氧预压涡轮压比对频率特性的影响在高入口压力条件下,氧预压涡轮压比会减小,因此对不同的氧预压涡轮压比进行静态参数平衡,获取动态模型系数,假设在不同氧预压涡轮压比下,流体的声速、含气条件、泵汽蚀特性不变,仅对涡轮压比进行单因素分析,得到试车台条件下发动机氧预压涡轮泵转速随氧贮箱压力脉动的幅频曲线如图5所示。涡轮压比与涡轮燃气绝热功的关系式[25]为
L=k/(k-1)RT(1-1/(πT(k-1)/k))(8)
式中:R和T分别为涡轮静子入口气体常数和燃气温度; πT为涡轮压比。
根据式(8)得到涡轮燃气绝热功与涡轮压比的曲线如图6所示,其中红色圈为涡轮压比9.10,蓝色方框为压比11.14。
图5 不同氧预压涡轮压比下液氧路幅频曲线
Fig.5 Amplitude frequency curves of liquid oxygen feed system under different oxygen pre—pressurized turbine pressure ratios
图6 燃气绝热功与涡轮压比关系曲线
Fig.6 Relationship between gas adiabatic work and turbine pressure ratio对比图5和图6可以看出,在11 Hz处,氧预压涡轮压比为9.10的幅值约为11.14的1.68倍,说明氧预压涡轮低压比对系统的振荡起到一定的贡献。随着涡轮压比的降低,燃气绝热功与涡轮压比曲线的斜率变大,当氧预压涡轮压比为9.10时,该阶段涡轮燃气绝热功下降的速率更大,这可能会导致氧预压涡轮泵出现非稳态工作点,从而使得11 Hz脉动的幅值加大。
从图5可以看出氧预压涡轮压比对系统的影响,在全频率范围段的增幅基本相当,说明氧预压涡轮压比的减小,在任何频率下,均会削弱系统的稳定性,但对系统的频率无影响。
2.2.2 氧预压泵动态增益的影响泵动态增益系数值的计算公式为
(9)根据以往的试验结果,选取m+1的范围,得到发动机氧预压涡轮泵转速相对于贮箱压力脉动的幅频曲线,如图7所示。在所有频率范围内,其幅值随着氧预压泵动态增益系数的变大而增大,而系统的谐振频率则有所降低。
图7 不同氧预压泵动态增益下液氧路幅频曲线
Fig.7 Amplitude frequency curves of liquid oxygen feed system under different dynamic gain of oxygen pre—pressurized pump2.2.3 氧预压泵后燃气掺混的影响氧预压涡轮泵对主路液氧增压,从而确保主泵入口液氧的压力足够高而不会发生严重汽蚀,氧预压涡轮由来自主涡轮后燃气导管的少量富燃燃气驱动,在其出口,做功后的富燃燃气经集合器通过管壁小孔注入液氧主路,进而使氧预压泵后的管路有一段为气液两相流,这段气液两相流会增加流体的柔度,从而影响系统的频率特性。在简化分析中,对氧预压泵后的燃气掺混一般采用等效声速和燃气穿透长度来表现,燃气穿透长度指从氧预压泵到燃气全部溶解处的流路长度,因此就燃气穿透长度和燃气掺混段声速对系统频率特性的影响进行分析。
图8和图9是不同燃气穿透长度和燃气掺混段声速的氧预压泵转速相对于贮箱压力脉动的幅频曲线。通过图8可以看到随着燃气穿透长度的增加,系统的一阶频率和二阶频率都降低了,这是因为当燃气穿透长度增加时,燃气掺混段的含气率升高,导致流体的柔度升高,从而降低了系统的谐振频率。同时,燃气中分布的均匀气泡具有降幅的作用,含气量越大,降幅作用越明显,脉动幅值也越小,所以当燃气穿透长度增加时,流体中的均匀气泡增多导致幅值降低。通过图9可以看到,随着燃气掺混段声速的增加,系统的谐振频率升高,同时脉动幅值也升高,其机理与燃气穿透长度改变系统的频率特性基本一样。总之,氧预压泵后的燃气掺混段对于发动机的频率特性有很大影响。
图8 不同燃气穿透长度液氧路幅频曲线
Fig.8 Amplitude frequency curves of liquid oxygen feed system under different gas penetration length
图9 燃气掺混段不同声速液氧路幅频曲线
Fig.9 Amplitude frequency curves of liquid oxygen feed system under different sound velocities in gas mixingsection- [1] HOLSTER J.Liquid rocket propellant feedline dynamics[C]//9th Propulsion Conference.Las Vegas,NV,Reston,Virigina: AIAA,1973.
- [2] ORDONNEAU G.A new numerical method for pogo analysis[C]//30th Joint Propulsion Conference and Exhibit.Indianapolis,Reston,Virigina: AIAA,1994.
- [3] 孙冰,魏鑫,池元成,等.液体运载火箭推进系统固有频率的通用化计算研究[J].导弹与航天运载技术,2009(1):38-40.
- [4] 刘上,刘红军,王海燕.富氧燃气发生器液氧供应系统频率特性分析[J].火箭推进,2013,39(2):12-18.
- [5] 陈琪锋, 刘昆, 张育林. 基于分布参数线性化模型的分级燃烧循环液体火箭发动机频率特性计算[J]. 航空动力学报,2001,16(1):44-48.
- [6] 荣克林,张建华,马道远,等.CZ—2F火箭POGO问题研究[C]//2007全国结构动力学学术研讨会论文集.南昌: 全国结构动力学学会,2007.
- [7] 盛迪南.流体系统的动特性分析(矩阵法)[Z].1985.
- [8] 秦澍纪.输送系统的动特性分析[Z].1985.
- [9] 吴天城.推进剂输送管路系统的动态试验[Z].1985.
- [10] 钱大馨.输送系统动态试验研究(水试)[Z].1985.
- [11] 廖少英. POGO蓄压器变频降幅特性分析[J]. 上海航天,2002,19(1):32-35.
- [12] 任辉,任革学,荣克林,等.液体火箭Pogo振动蓄压器非线性仿真研究[J].强度与环境,2006,33(3):1-6.
- [13] 万屹仑,付欣毓,张黎辉,等.注气式蓄压器系统工作特性仿真分析[J]. 火箭推进,2018,44(3):37-42.
- [14] 张黎辉,张振鹏.补燃循环液体火箭发动机输送系统的频率特性[J].推进技术,2000,21(1):5-7.
- [15] 邢理想.闭式循环液体火箭发动机氧路低频动特性分析[D].西安:西安航天动力研究所,2009.
- [16] 邢理想,杜大华,李斌.液氧/煤油补燃火箭发动机氧路低频动特性分析[J].火箭推进,2009,35(5):24-28.
- [17] 张淼,李斌,邢理想.基于燃气射流冷凝的氧路系统频率特性研究[J].航空学报,2020,41(2):142-151.
- [18] 杜大华,张继桐.液压流体系统的频域特性分析[J].机床与液压,2006,34(10):86-88.
- [19] BRENNEN C,ACOSTA A J.The dynamic transfer function for a cavitating inducer[J].Journal of Fluids Engineering,1976,98(2):182-191.
- [20] BRENNEN C.Bubbly flow model for the dynamic characteristics of cavitating pumps[J].Journal of Fluid Mechanics,1978,89(2):223-240.
- [21] 李斌,杜大华,张贵田,等.液氧/煤油补燃发动机低频频率特性研究[J].航空动力学报,2009,24(5):1187-1191.
- [22] 格列克曼Б Ф.液体火箭发动机自动调节[M].顾明初,译.北京:宇航出版社,1995.
- [23] 徐浩海,刘站国.液氧/煤油补燃发动机系统稳定性分析[J].火箭推进,2005,31(2):1-6.
- [24] 张黎辉,张振鹏.补燃循环液体火箭发动机系统的响应特性研究[J].航空动力学报,1999,14(4):425-428.
1.1 系统流路图1为某型液氧/煤油补燃循环发动机氧路系统简图,虚线方框内为本文研究对象,其主要流路为贮箱供应的液氧经由主管路、过滤器和波纹管后到达氧预压泵,由氧预压泵增压后流经一段管路到达氧主泵。氧预压涡轮为气涡轮,由主涡轮后燃气导管引出的富氧燃气驱动,经由氧预压涡轮做功后的燃气在氧预压泵后与液氧主路进行掺混。液氧路系统以液氧贮箱、氧主泵作为边界; 燃气路以氧预压涡轮入口为恒压源。由发动机的氧路系统图中抽象出本文研究的液氧供应系统的流路图,如图2所示。
图1 液氧/煤油补燃循环发动机氧路系统简图
Fig.1 Schematic of oxygen system for LOX/kerosene staged combustion cycle engine
图2 发动机液氧供应系统流路图
Fig.2 Schematic of liquid oxygen feed system in engine1.2 发动机线性化小偏差传递矩阵模型1.2.1 液路直管假设直管的管壁为刚性, 流动为轴对称层流, 流体黏性不变。根据一维流动的Novier—Stokes(N—S)方程、连续方程和状态方程,经过解偏微分方程、线性化、无量纲化得到直管的分布参数的传递矩阵方程为[18]
(1)式中:δp、δq分别为压力和流量的无量纲脉动量; Zc为流体特征阻抗,Zc=a/A,其中a和A分别为管路流体声速和管路截面积;
和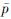
分别为流体的平均流量和压力; l为管路长度。1.2.2 泵
泵过流体为复杂的三维流动,用于发动机系统分析和控制时,三维的N—S方程过于复杂,无法直接应用,所以一般采用四端传递矩阵形式进行描述[19-20]。考虑泵的汽蚀过程,建立汽蚀泵的传递矩阵方程,其表达式为
式中:m+1为动态增益; Cb为汽蚀柔度; Rp为阻力; Mb为质量流量增益; δn为转速的无量纲脉动量; Zp为泵的阻抗,Zp=Rp+sLp; Lp为惯性; p1、p2和q分别为泵入口、出口压力和泵的流量; s为拉普拉斯算子;
。氧主泵的大流阻环节作为系统的闭端边界,其汽蚀区在入口,因此在计算时需考虑氧主泵的汽蚀柔度影响。
1.2.3 涡轮在描述低频流体动力学过程中,不考虑涡轮泵轴的功率平衡及振动影响,在线性小偏差范围内进行分析,可得涡轮的无量纲传递矩阵方程为[21]
(3)其中
εt=((k+1)((pet)/(pit))(k-1)/k-2)/(2k[1-((pet)/(pit))(k-1)/k])
式中:δT为温度的无量纲脉动量; T1、T2分别为涡轮入口和出口的静温; εt为通过涡轮的燃气流量与涡轮压比曲线的无量纲斜率; k为绝热指数; pit、pet分别为涡轮入口和出口压力。
1.2.4 氧预压涡轮泵功率平衡方程对于涡轮泵的功率平衡方程大都采用转速变化率与涡轮、泵转矩之间的关系[22-24]。假设氧预压涡轮泵转子作为一个整体转动,根据能量守恒可以得到涡轮泵的功率平衡方程,即
J(dω)/(dt)=Mt-Mp(4)
其中
Mt=Lqtη/ω
Mp=Mp(n,q)
式中:J、ω分别为氧预压涡轮泵的转动惯量和轴角速度; Mt、Mp分别为氧预压涡轮和氧预压泵的扭矩; L、qt、η分别为氧预压涡轮的绝热功、流量和效率; n为氧预压涡轮泵转速; q为预压泵的流量。
将上式线性化、无量纲化和拉普拉斯变换后可得频域的氧预压涡轮泵系统的动态特性方程
(π2Jn2)/(900Pt)sδn=[1+βt-0.5ψtβt+εt]δpit-[βt-0.5ψtβt+εt]δpet+0.5(1-ψt)δTit+ψtδn-(Pp)/(Pt)(ψqPδqeppo+ψnPδn)(5)
其中
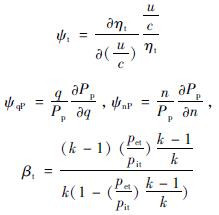
式中:Pt、Pp分别为氧预压涡轮和预压泵的功率; δpit、δpet、δTit、δqeppo和δn分别为氧预压涡轮入口和出口的压力脉动、氧预压涡轮入口的温度脉动、氧预压泵出口的流量脉动和氧涡轮泵的转速脉动; ψt为氧预压涡轮效率ηt和u/c比值的无量纲斜率。
1.2.5 边界干扰量的确定发动机频率特性分析时,合理的边界干扰量的确定是获得准确频率特性的关键。对于本文的分析对象,液氧贮箱作为大容腔边界,其入口压力脉动为零,入口压力脉动可作为一个干扰量; 氧主泵作为高转速元件,对压力波有较强反射效果,泵可近似为上游扰动波的声学闭端,即流量脉动等于零,因此系统出口流量脉动可作为一个干扰量; 预压涡轮入口燃气,从大容腔的主燃气通道引流,可认为其压力脉动为零,则涡轮入口压力脉动可作为一个干扰量。
1.2.6 仿真方法将发动机贮箱到氧主泵入口之间的组件方程整理后,为一组含有13个方程的方程组,方程均为带有复系数的线性代数方程。可化为矩阵方程
W(ω)δx=dδy(6)
式中:W(ω)为系统各组件方程复系数矩阵; δx为系统参数变化量的矢量; d为数学模型方程中各外部干扰作用系数矩阵; δy为外部干扰作用变化量。
在振幅为δyj的第j个干扰的影响下,求系统第i个参数振幅δxi的解,利用关系式[22]
(δxi)/(δyj)=(Δij)/Δ=Reij(ω)+iImij(ω)=Aij(ω)exp[-iφij(ω)](7)
式中:Δ为W(ω)的行列式; Δij为行列式Δ第i列换为矩阵d的第j列而得到的行列式; Reij(ω)、Imij(ω)为传递函数的实部和虚部; Aij(ω)、φij(ω)为幅频特性和相频特性。
在解题条件所确定的范围内对于一系列强迫振荡频率求解式(7),可得发动机频率特性。
