作者简介:石波(1980—),男,硕士,高级工程师,研究领域为冲压发动机总体。
1.西安航天动力研究所,陕西 西安 710100; 2.火箭军装备部驻西安地区第二军事代表室,陕西 西安 710100
1.Xi'an Aerospace Propulsion Institute,Xi'an 710100,China; 2.The 2nd Military Represent Office of the Rocket Force Equipment Department in Xi'an,Xi'an 710100 China
airbreathing engine; variable nozzle; divergent flap; multi-objective optimization; topology optimization
备注
作者简介:石波(1980—),男,硕士,高级工程师,研究领域为冲压发动机总体。
针对某吸气式发动机可调喷管的扩张调节片开展结构优化研究。根据调节片加筋结构常规布局形式,用壳单元和梁单元来代表薄板和加强筋,建立参数化设计模型,开展多目标优化设计得到常规布局的结构设计方案。通过结构拓扑优化设计并对优化结果进行二次建模,得到工程可行的结构优化方案。对2种方法得到结构方案进行对比,拓扑优化结构方案重量减少14.8%,最大变形减少38%,最大结构应力相当但结构应力分布更加均匀。拓扑优化设计得到的结构方案具有材料利用率高、结构轻、性能好的优点,对于喷管调节片薄壁加筋结构优化问题拓扑优化方法具有良好的工程应用前景。
The structure optimization for divergent flap on variable nozzle of airbreathing engine was studied.According to the conventional stiffener layout of adjusting flap,the parametric model was established.In this model,shell element and beam element were used instead of thin-walled structure and stiffener.Through the multi-objective optimization of this model,the structure scheme of conventional layout was obtained.Topology optimization for divergent flap was carried out.The feasible structure was obtained by re-modeling.By comparing the structures obtained by the above two methods,the weight is reduced by 14.8%,the maximum deformation is reduced by 38%,and the maximum structural stress is equivalent,but the structure stress distribution is more uniform in the topology optimization scheme.The structure scheme by topology optimization has the advantages of high material utilization,light weight and good performance.For the optimal design of thin-walled stiffened structure of variable nozzle flap,the topology optimization has a good prospect in engineering application.
引言
0 引言
超声速、高超声速飞行器装备的吸气式发动机常采用可调收—扩超声速喷管,使得气流尽可能膨胀,从而获得高的推力特性和发动机性能[1]。喷管设计往往以高性能为目标,综合考虑结构质量、复杂性、可靠性、维修性及成本多种因素[2]开展设计工作。在满足各项性能要求情况下对喷管结构开展减轻质量工作,喷管调节片(含收敛—扩张调节片和密封片)是重点关注的零组件。
可调喷管调节片主要采用薄壁加筋板壳结构,具有结构效率高、质量轻的特点。薄壁加筋结构优化主要研究两方面问题:加筋结构的空间布局优化和薄壁厚度/加强筋截面的尺寸参数优化。近年来国内外专家针对薄壁加筋结构优化开展大量工作:Stok等用优化准则法分阶段对板壳厚度进行优化从而确定加强筋布局位置[3]; Lam等用变厚度法优化板壳,然后基于工艺限制条件对加强筋结构参数和间距进行优化设计[4]; 刘齐茂等用壳单元和梁单元来代表薄板和加强筋,通过改变梁单元高度使梁单元截面边缘应力达到屈服极限的方法得到加强筋的分布形态[5]。学者们模仿生物体结构开展加强筋分布优化设计[6-8]或模拟生物自适应生长规律,以最小柔度为目标让加强筋沿着结构应变能相对于其截面积的设计灵敏度大的方向扩展,从而得到加强筋分布形态[9]; 王栋等提出了将加强筋等效为弹性铰(点)支撑的简化模型,依据加筋横向移动的灵敏度信息优化加强筋位置,最后优化加强筋高度的分步优化方法[10]; 张卫红等提出了几何背景网格法的拓扑优化方法,以结构刚度最大为设计目标针对平面及曲面薄板开展了加筋优化设计,对航空发动机喷管收敛调节片开展多工况组合条件下的加筋布局优化[11]; 钟焕杰等提出通过编程求解最优加筋比和厚度比,结合拓扑优化开展薄板加筋结构设计的方法[12]。综合以上文献资料,得到以下结论:
1)加筋结构的空间布局优化在加筋结构优化设计中的作用十分关键,直接影响了优化结果的优劣,因此成为中外学者研究的重点;
2)生物仿生类算法存在仿生原型难获取、优化准则和算法复杂、优化结果结构复杂及生产工艺性差的问题,工程应用范围比较窄;
3)建立薄壁加筋结构的参数化模型比较复杂,一般适用于加强筋分布形式比较规则的情况,常常采用近似简化模型;
4)拓扑优化方法工程适用范围广,效果好,但存在算法复杂、编程计算难度大、优化得到的加筋分布不清晰、筋截面不连续/不均匀的缺点,需要对优化结果进行二次建模处理。
本文以某发动机可调喷管的扩张调节片为算例,根据调节片加筋结构正置正交网格和斜置对称方格的常规结构布局形式,基于ANSYS Workbench平台用壳单元和梁单元来代表薄板和加强筋建立了参数化设计模型; 在典型工况力热载荷下,以结构最大刚度和最小化应力为设计目标,结构质量和变形位移为设计约束,开展多目标优化设计得到常规布局的结构设计方案。通过Optistruct软件开展结构拓扑优化设计,利用OSSmooth工具对优化结果进行处理得到了工程上可行的加强筋结构优化方案。对两种方法得到结构方案通过仿真计算开展性能对比研究。
1 可调喷管的扩张调节片算例
1.1 结构简介某发动机的收敛—扩张喷管结构由喷管本体(含收敛—扩张调节片、密封片及连接机构)、作动机构(含作动筒、调节同步环)组成,其中收敛—扩张调节片和密封片各24片,间隔圆周对称分布,通过机械定位和气动定位相结合的方式确定喷管喉道面积。喷管调节片运动机构由收敛调节片、扩张调节片、连杆组成四连杆机构,在作动筒的驱动下对喉道面积和出口面积进行调节,结构示意图如图1所示。
2 调节片常规布局多目标优化
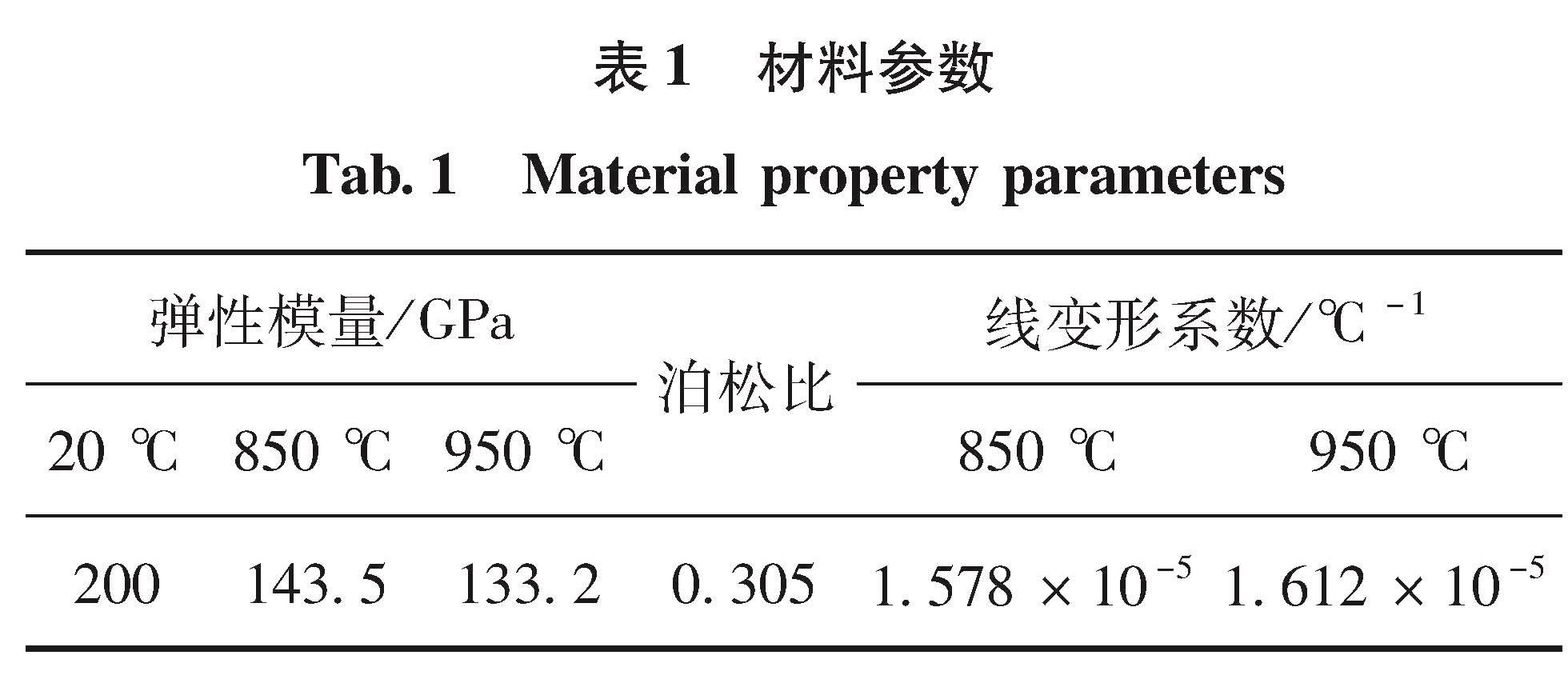
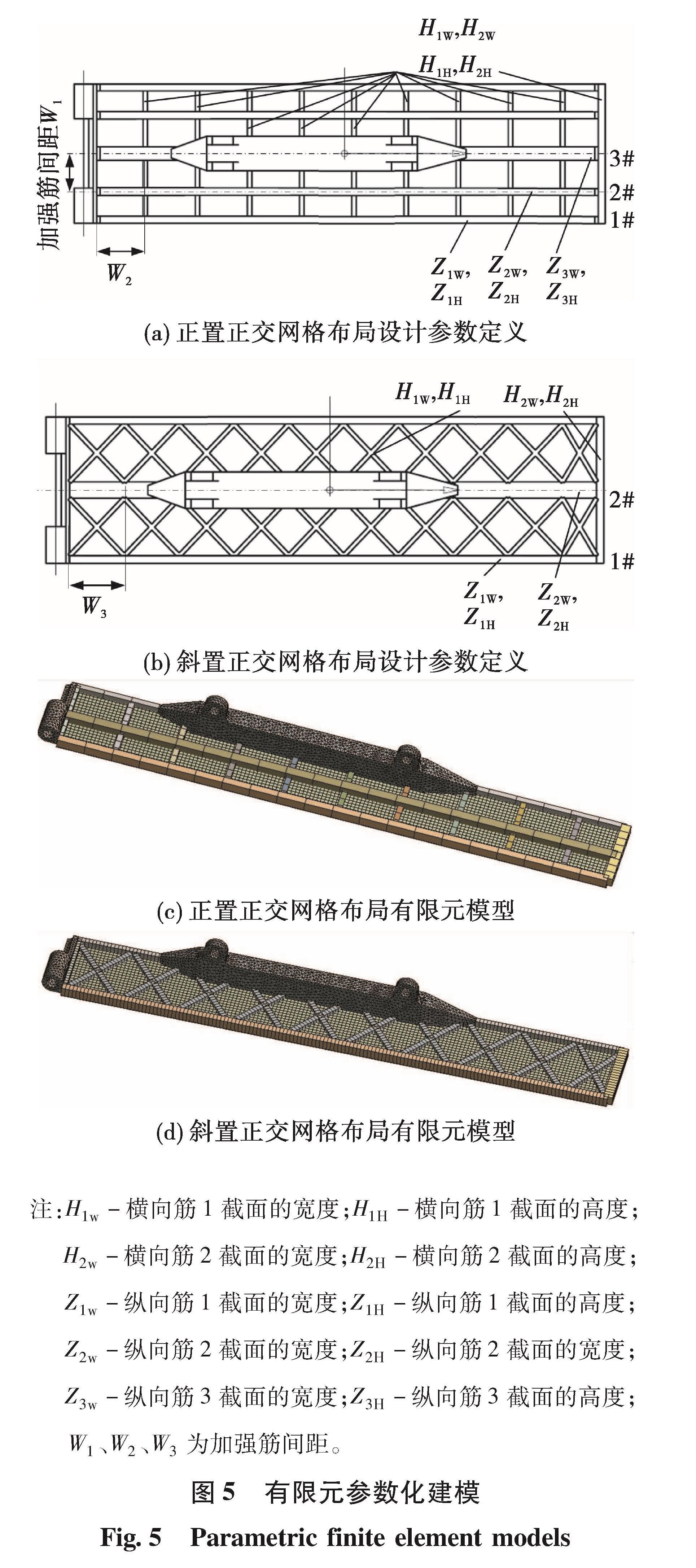
2.1 有限元建模薄壁加筋结构常采用正置正交网格、斜置正交网格两种形式,斜置正交网格多采用±45°正方形网格形式[13],参考这些布局形式,基于ANSYS Workbench平台用壳单元和梁单元来代表薄板和加强筋建立了调节片薄壁加筋结构的参数化设计模型[14],如图5所示。考虑到调节片为对称结构,建模时只取对称结构的1/2建立模型[15]。因加强筋的间距直接影响了加强筋的数量和布局形式,因此可以通过根据不同间距参数建立多个模型开展优化计算,从中挑选最佳布局方案的方法确定加强筋间距。为减少设计变量,提高计算效率,本文对横向筋截面和斜向筋截面进行了同截面假设。可以将所有筋截面设置成设计参数,通过参数关联性计算参数灵敏度[16],优选出部分设计参数进行多目标优化[17],但这种方法往往需要付出较大的计算代价。
2.2 多目标优化对调节片结构开展多目标优化设计,将结构最大变形做为结构的刚度指标,以最小化结构最大变形和最大应力做为设计目标,以调节片厚度、加强筋的结构参数、调节片结构质量指标做为约束条件,优化模型的数学表达式为
min max δ(ZW,ZH,XW,XH,t)(1)
min max σ(ZW,ZH,XW,XH,t)(2)
 (3)
(3)式中:max δ为结构最大变形量,mm; max σ为结构最大应力,MPa; M为结构总质量,kg; M0为结构质量指标,kg; ZWi为纵向筋截面的宽度,mm; ZHi为纵向筋截面的高度,mm; XWj为横向/斜向筋截面的宽度,mm; XHj为横向/斜向筋截面的高度,mm; n为纵向筋的数量; m为横向/斜向筋的数量; lbi,lbj为取值下限,mm; Ubi,Ubj为取值上限,mm; t为调节片底板厚度,mm。
ANSYS Workbench软件平台的优化工具Design Exploration的设计流程[18]为建立参数化模型,设置参数关联性和参数变化范围,调用实验设计(DOE)模块在设计域内挑选设计点生成样本空间,调用响应面(Response Surface)模块构造设计输入参数和设计输出参数的函数关系,最后调用优化模块(Optimization)开展多目标优化设计。
样本点在设计空间中的分布情况制约着响应面函数的拟合精度[19]。在实验设计(DOE)模块中,调用了中心复合设计(CCD)[20],该方法常用于已知模型响应面为二阶的情况。针对两水平全因子的中心复合试验设计方法可产生m=2n+2n+1个样本点。选用二阶响应面,其函数表达式[21]如下
 (4)
(4)式中:β0、βi、βii、βij为多项式待定系数; ε为函数y的误差; Xi为设计变量; k为设计变量的数量。
通过响应面拟合模块计算,得到设计输入参数对输出参数的灵敏性分析,如图6所示。由于设计变量过多,图6中只列出部分设计输入参数对输出参数的灵敏性分析结果。
3 调节片拓扑优化
拓扑优化的目的是寻求结构在设计空间最佳的分布形式,或在设计空间内寻求结构最佳的布置方式,以优化结构的某些性能或减轻结构的质量。目前主要有三大类拓扑优化方法:
1)均匀化方法[22];
2)密度法(artificial materials,最具代表的各向正交惩罚材料密度法,即SIMP[23]);
3)变厚度法[24]。
OptiStruct[25]是CAE软件HyperWorks平台下的以有限元法为基础,面向产品设计、分析和优化的有限元和结构优化求解器,用于进行结构拓扑优化概念设计和细化设计。
3.1 拓扑优化数学模型及初始定义OptiStruct中目标函数和约束函数可以用结构的质量、体积、结构位移、应力、应变、温度、频率(结构模态分析对应模态的频率)、屈曲因子等。参考前面常规布局多目标优化的计算结果,将拓扑优化的数学模型定义为满足位移约束、应力约束下的结构质量最小。初始模型及设计域定义如图7所示。考虑到加工工艺要求,设置单向拔模约束。
本算例采用了多设计域定义,根据工艺和生产制造原因合理分割了所需优化的空间,便于在拓扑优化求解时可以灵活地设置工艺约束条件。
3.2 拓扑优化计算过程不同设计工况和不同制造工艺约束组合下的拓扑优化计算结果如图8所示。工况分为只考虑调节片气动载荷(工况1)、只考虑密封片对调节片的作用力(工况2)和高温温度场下的力热联合载荷(工况3)3种工况。图8中不同工况下生成的加强筋的形态是不同的。
本算例涉及的制造工艺约束主要是最小成员尺寸Dmin、最大成员尺寸Dmax和拔模约束。最小成员尺寸的作用是消除细小传力路径,便于铸造过程材料流动和提供足够刚度便于道具加工,对应3D打印的材料最小成型精度。最大成员尺寸的作用消除优化结果中的材料堆积,提供多个传力路径。拔模约束主要考虑加工过程拔模和刀具进出,适用于实体表面生成加强筋结构。从图8(e)结果可见,不考虑拔模约束,生成的加强筋结构为“空腔夹层”结构,除了采用3D打印,其他加工方式很难加工。
在拓扑优化过程中,设计人员需要不断调整制造工艺约束、设计域、模型计算网格、约束条件等参数,通过多次迭代,最终获得满足各项设计要求的优化结果。
3.3 拓扑优化结果处理拓扑优化计算结果是单元密度不同的网格数据,存在不光滑、不连续和不清晰的情况。调用OptiStruct软件的OSSmooth工具可以根据单元密度结果生成封闭的等值曲面,然后可以将模型导出到UG软件中重新建模,得到工程上可行的加强筋结构优化方案。调节片常规布局结构和拓扑优化结构对比如图9所示。
4 优化结果对比
5 结论
1)在薄壁加筋结构优化设计中,加筋结构的空间布局优化十分关键,对优化结果的优劣有决定性影响。拓扑优化设计得到的结构方案具有材料利用率高、结构轻、性能好的优点,拓扑优化方法针对喷管调节片薄壁加筋结构优化问题具有良好的工程应用前景。
2)在拓扑优化设计中,对制造工艺约束、设计域、模型计算网格、约束条件等初始条件定义不同,会得到不同的设计结果。设计人员需要结合工程实践经验,采用多方案、不同参数组合、多轮迭代的方法,优选出最佳方案。
- [1] 梁俊龙,吴宝元,李斌.几何结构可调的亚燃冲压发动机性能研究[J].火箭推进,2010,36(2): 1-4.LIANG J L,WU B Y,LI B.Performance research of adjustable geometric structure ramjet engine[J].Journal of Rocket Propulsion,2010,36(2): 1-4.
- [2] 刘大响.航空发动机设计手册第7册:进排气装置[M].北京:航空工业出版社,2000.
- [3] STOK B,MIHELIC A.A two-stage design optimization of shell structures[C]//Developments in Computational Engineering Mechanics.Edinburgh,United Kingdom.Stirlingshire: Civil-Comp Press,1983.
- [4] LAM Y C,SANTHIKUMAR S.Automated rib location and optimization for plate structures[J].Structural and Multidisciplinary Optimization,2003,25(1): 35-45.
- [5] 刘齐茂,燕柳斌.基于边缘纤维屈服准则的薄板结构加强筋的优化设计法[J].机械设计,2007,24(4): 33-34.
- [6] 赵岭,陈五一,马建峰.基于王莲叶脉分布的机床横梁筋板结构仿生优化[J].高技术通讯,2008,18(8): 806-810.
- [7] 杨永彬,陈五一,赵大海.机床立柱高比刚度结构仿生设计[J].北京航空航天大学学报,2008,34(9): 991-994.
- [8] 岑海堂,陈五一.小型翼结构仿生设计与试验分析[J].机械工程学报,2009,45(3): 286-290.
- [9] 丁晓红,李国杰,蔡戈坚,等.薄板结构的加强筋自适应成长设计法[J].中国机械工程,2005,16(12): 1057-1060.
- [10] 王栋,李正浩.薄板结构加筋布局优化设计方法研究[J].计算力学学报,2018,35(2): 138-143.
- [11] 张卫红,章胜冬,高彤.薄壁结构的加筋布局优化设计[J].航空学报,2009,30(11): 2126-2131.
- [12] 钟焕杰,金海波.基于拓扑优化的薄板加筋方法研究[J].机械设计与制造工程,2015,44(1): 41-45.
- [13] 张俊华,张绪香,吕玉林,等.导弹结构强度计算手册[M].北京:国防工业出版社,1975.
- [14] 赵阳, 许博谦, 李玉韦. 航天半硬壳结构模型简化方法研究[J]. 长春理工大学学报(自然科学版), 2019, 42(3): 1-6.
- [15] 王玉新. 喷气发动机轴对称推力矢量喷管[M]. 北京: 国防工业出版社, 2006
- [16] 胡建平, 黄磊, 王留柱, 等. 基于参数敏感度分析的移栽机提升支架轻量化设计[J]. 机械设计与制造, 2017(1): 38-42.
- [17] 艾延廷, 刘海月, 田晶, 等. 薄壁机匣螺栓连接结构多目标优化设计[J]. 推进技术, 2019, 40(4): 876-883.
- [18] 付稣昇.ANSYS workbench 17.0数值模拟与实例精解[M].北京:人民邮电出版社,2017.
- [19] 于嘉腾.基于可靠性优化的机翼设计研究[D].沈阳: 沈阳航空航天大学,2015.
- [20] 张雷,张立华,王家序,等.基于响应面的柔轮应力和刚度分析[J].浙江大学学报(工学版),2019,53(4): 638-644.
- [21] 唐林,许志沛,贺田龙,等.基于响应面法的多节伸缩臂设计优化[J].机械设计与制造,2020(2): 83-86.
- [22] BENDSØE M P,KIKUCHI N.Generating optimal topologies in structural design using a homogenization method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(2): 197-224.
- [23] 何芝,雷阳,封硕,等.基于SIMP法的变刚度结构拓扑优化研究[J].装备制造技术,2020(1): 8-14.
- [24] 程耿东,张东旭.受应力约束的平面弹性体的拓扑优化[J].大连理工大学学报,1995,35(1): 1-9.