作者简介:杨建文(1984—),男,硕士,高级工程师,研究领域为液体火箭发动机流动、传热与燃烧。
(Science and Technology on Liquid Rocket Engine Laboratory,Xi'an Aerospace Propulsion Institute,Xi'an 710100,China)
备注
作者简介:杨建文(1984—),男,硕士,高级工程师,研究领域为液体火箭发动机流动、传热与燃烧。
通过对室压8.5 MPa、基准喷管面积比为30、喷管总面积比100的双钟形喷管进行设计和性能分析,结果表明:喷管延伸段采用抛物线法、圆弧法、最大推力喷管型面压缩法以及等角度法四种方法设计的双钟形喷管比冲性能相差小于1 m/s,等角度法在4种设计方法中比冲性能最高; 从海平面到6 km高度左右时,由于喷管延伸段会产生附加阻力损失,双钟形喷管的比冲比基准喷管的比冲平均低约1.5%左右; 在飞行高度7~12 km之间,双钟形喷管出口压力低于环境压力,双钟形喷管比冲低于基准喷管,在8 km高度双钟形喷管比冲比基准喷管比冲低约9.28%; 随着飞行高度的增加,从12 km左右开始,双钟型喷管的比冲高于基准喷管的比冲,到50 km后,双钟型喷管的比冲比基准喷管比冲高约10.69%。
Different dual-bell nozzles were designed with the benchmark nozzle area ratio of 30 and total nozzle area ratio of 100,and their performance were analyzed with a chamber pressure of 8.5 MPa.The results show that the difference of specific impulse performance of dual-bell nozzles designed by four methods of parabolic method,circular arc method,maximum thrust nozzle optimized with contour compression method and equal angle method is less than 1 m/s in the nozzle extension section.The specific impulse performance of equal angle method is the highest among four design methods.When the altitude is from sea level to around 6 km,the specific impulse of dual-bell nozzle is lower than the benchmark nozzle about 1.5% due to the additional drag loss caused by the nozzle extension contour.Between the flight altitudes from 7 km to 12 km,the outlet pressure of the dual-bell nozzle is lower than the ambient pressure,and the specific impulse of dual-bell nozzle is about 9.28% lower than the benchmark nozzle at the flight altitude of 8 km. As the flight altitude increases,the specific impulse of dual-bell nozzle is higher than the benchmark nozzle from 12 km. After 50 km,the specific impulse of dual-bell nozzle is about 10.69% higher than the benchmark nozzle.
引言
对于液体火箭发动机,采用传统的拉瓦尔喷管,如果喷管面积比过小,飞行过程中燃气未完全膨胀会造成部分比冲损失,如果面积比过大,飞行过程中由于燃气过膨胀会导致喷管发生流动分离、产生侧向载荷,严重时会直接破坏发动机的结构。为了使发动机喷管产生的比冲效益最大化,高度补偿喷管方案应运而生,这些方案包含双钟形喷管、塞式喷管、缝隙式喷管、变几何结构喷管等。双钟形喷管具有结构简单、总冲性能提升较大等优点,目前成为研究发动机性能增长的一种重要手段。
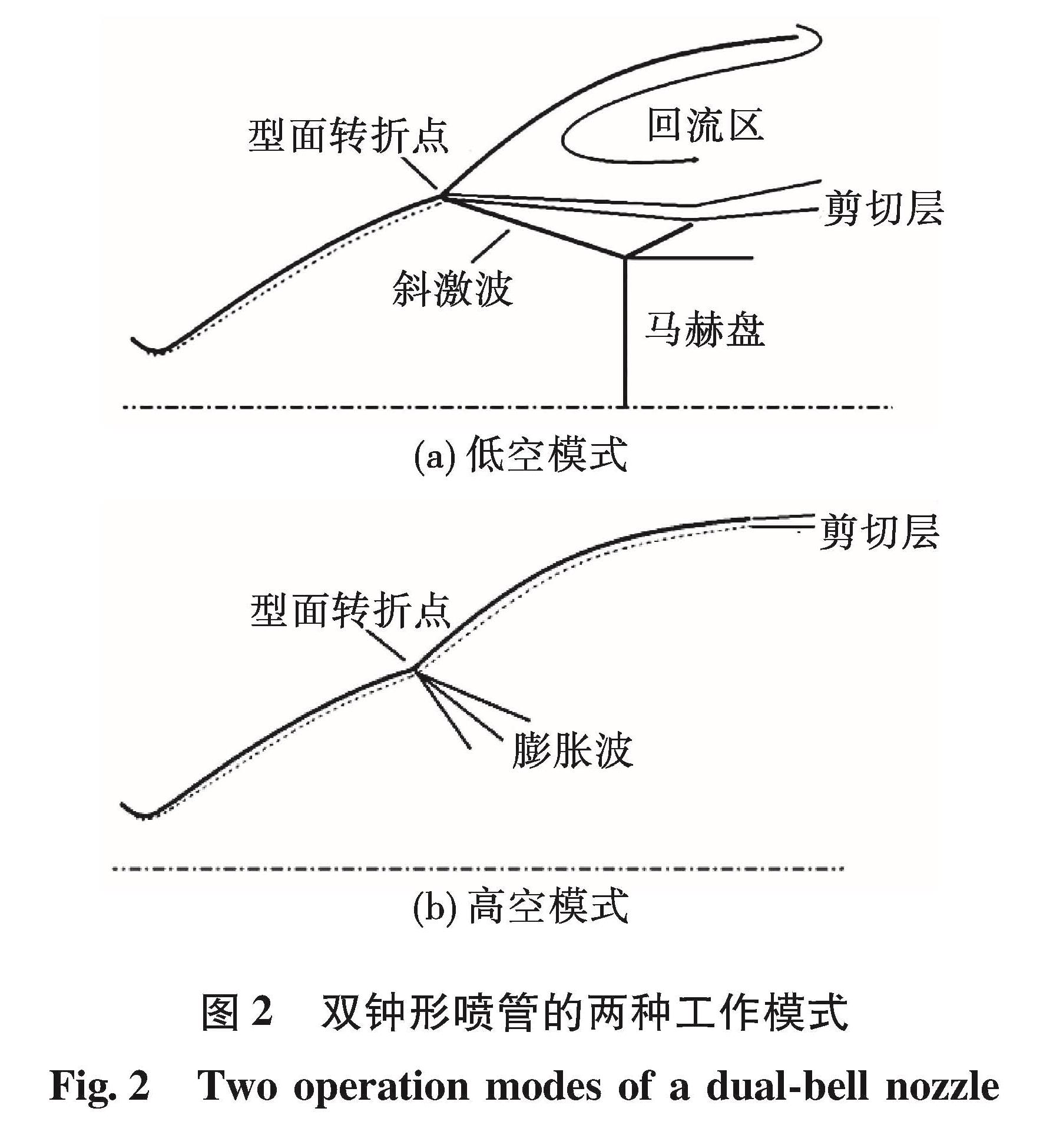
双钟形喷管(见图1)包括基准喷管和喷管延伸段。双钟形喷管在低空工作模式时,被控制的轴对称流场在反射作用下出现分离,产生较小的有效面积比见图2(a); 在高空工作模式时,随着高度增加和气体进一步膨胀,转折处下游的流动逐渐向喷管贴紧,直至气流充满整个喷管出口截面,使用了全部的面积比见图2(b); 由于面积比较大,可以得到比海平面工作时更好的性能[1]。
第一个双钟形喷管是Horn和Fisher提出并公布的[2],目前国外研究主要集中在美国洛马、NASA、德国DLR、意大利罗马大学、俄罗斯莫斯科航空学院等[3-17]。
Hagemann和Frey等基于理论分析和数值模拟开展了双钟形喷管的设计,然后在DLR的P6.2冷气测试试验台上进行了大量的缩尺冷气试验[14]。俄罗斯科尔得什研究中心及莫斯科航空学院针对双钟形喷管,开展了型面设计研究、性能仿真分析及双钟形喷管的转捩流动仿真分析和实验研究。他们主要采用差动喷管试验台开展相关实验研究。
意大利罗马大学主要和DLR合作开展了双钟形喷管的设计优化及流场仿真计算方面的研究[15]。日本学者Miyazawa针对H-2A火箭的LE-7A发动机,采用双钟形喷管方案时,与原喷管相比,发动机可以得到10 s的比冲收益[16]。马歇尔空间飞行中心采用F-15战斗机进行了双钟形喷管挂载飞行试验,发现其在不同条件下均拥有高于传统喷管的性能[17]。
国内对于双钟形喷管的研究比较零散。郑孟伟等对双钟形喷管在不同环境压力下的流场进行数值模拟,并与相应的冷吹风试验结果进行对比验证 [18]。许晓斌等在CARDC超高速所FD-20A高超声速风洞中进行了双钟形喷管冷态模拟试验研究,对在冷态模拟条件下的喷流模拟技术、喷管推力测量试验技术和流动显示技术等进行了研究,其测量的准度和精度均可满足要求[19]。王一白等采用气氧作氧化剂、气氢作燃料,对具有高度补偿特性的塞式喷管和双钟型喷管进行了点火热试[20]。洪流开展了双钟形喷管的临界评估分析研究[21]。
综上所述,国外研究相对系统化,目前主要研究集中在双钟形喷管分离点转捩的安全性; 而国内最近几年研究很少,截至目前,还没有一个标准的设计方法。因此,本文针对双钟形喷管,基准喷管采用最大推力喷管型面,延伸段采用不同的设计型面; 比较了不同型面下双钟形喷管在不同高度下的比冲性能,确定了在所研究的范围内比冲最优的型面,为双钟形喷管型面设计提供必要的参考。
1 双钟形喷管设计
2 双钟形喷管性能分析
2.1 双钟形喷管性能计算方法获得双钟形喷管型面后,要进行性能评估才能评判各设计方法的优劣,因此,必须要研究双钟形喷管的比冲等性能计算和评估方法及手段。
对于双钟形喷管,其工作状态分为海平面到低空状态和高空状态,其中,海平面到低空工作时,双钟形喷管的基准喷管满流,而喷管延伸段不满流,高空工作时,双钟形喷管全部满流,因此,其在不同飞行高度时的推力计算方法不同,本文按照不满流和满流两种模式考虑。
在海平面到低空工作时,双钟形喷管中流场分离区内的压力稍低于环境压力,而喷管外壁面的压力是环境压力,使得分离区的喷管内外壁有一定的压差,导致有一定的推力损失,计算喷管比冲时,必须将这一部分推力损失去掉,通过分析,其比冲计算式为
Isp=Ve,D+((pe,D-palt)AD)/(m·)-(∫A EAD(palt-pe,w)dA)/(m·)(7)
式中:Ve,D是第一段喷管出口轴向速度; pe,D是第一段喷管出口压力; AD是第一段喷管出口面积; palt是环境压力; pe,w是喷管延伸段壁面压力; AE是双钟形喷管出口面积; m·是双钟形喷管流量。
在高空环境工作时,双钟形喷管满流,其比冲计算方法和传统的最大推力喷管计算方法一样,计算式为
Isp=Ve,E+((pe,E-palt)AE)/(m·)(8)
式中Ve,E是双钟形喷管出口轴向速度。
上述给出了理论计算公式,实际计算时,由于喷管延伸段壁面压力分布无法通过理论计算求解得到,此外,喷管出口轴向速度、压力沿着径向均是一条分布曲线,因此,直接采用理论公式计算结果误差较大。
随着计算气体动力学的日趋完善,对于喷管这种纯气动部件,其计算结果准确性也比较高,因此,本文开展了设计的4种双钟形喷管型面在不同飞行高度下的流场CFD仿真计算,获得了流场参数,为分析其在不同飞行高度下的性能参数提供输入参数。
2.2 双钟形喷管流场计算方法本文研究的双钟形喷管几何结构和流场结构是轴对称,因此采用多组分二维轴对称N-S方程,数值求解时,无黏通量的离散采用具有二阶TVD性质的HLLC格式,黏性通量离散采用中心差分格式,此外,为避免高阶精度格式下解在间断附近出现的非物理振荡,采用了Min-Mod限制器,湍流模型采用的是SST k-ω湍流模型。计算时,时间上采用点隐式方法进行迭代求解,直至流场收敛。
2.3 双钟形喷管流场计算方法验证采用文献[22]中的双钟形喷管对本文的计算方法进行了验证,双钟形喷管喉道半径10 mm、基础段喷管面积比11.3、延伸段面积比25.6、基础段喷管长度62 mm、延伸段长度83 mm、型面转折角7.2°,图5为仿真与试验壁面压力分布对比,可以看出,SA、SST、RNG 3种湍流模型均能够模拟出双钟形喷管特有的受控分离,且SST模型的结果与试验最为接近。综上所述,采用上述的计算方法能够准确计算双钟形喷管的流场。
2.4 双钟形喷管流场结构本文采用的是二维轴对称模型,网格采用的是四边形结构化网格,划分网格时,对壁面处进行了加密,壁面第一层网格高度小于0.2 mm,总网格数量超过2.08×105时,流场规律、边界层厚度等不再变化。基于此,本文所有模型的网格均采用壁面第一层网格高度0.1 mm、总数量2.54×105,对双钟形喷管流场开展模拟。
本文对上述设计的4种双钟形喷管开展了流场仿真,4种双钟形喷管的流场分布规律基本一致,本文只列出了采用轴向等角度变化设计的型面计算得到的流场马赫数,具体如图6所示。
图6 不同高度下双钟形喷管马赫数流场云图
Fig.6 Mach number distribution of dual-bell nozzle under different flight altitudes在地面和低空状态下[图6(a)和图6(b)]双钟形喷管在基准喷管满流,而在基准喷管与延伸段连接的型面转折点处由于环境压力的作用发生轴对称分离。喷管主流为激波和剪切层组合形成的串式结构。
随着飞行高度的增加,环境压力降低,主流逐渐膨胀,激波串结构向外推移,飞行高度到达8 km至10 km时[见图6(c)],流动在型面转折点处出现工况突跃,主流完全附着于喷管延伸段,双钟形喷管满流,此时,由于双钟形喷管出口压力较环境压力要低,双钟形喷管的比冲还低于基准喷管的比冲。
随着环境压力继续降低,飞行高度到达15 km后[见图6(d)、图6(e)和图6(f)],主流继续膨胀,喷管出口压力大于环境压力,喷管总面积比得到有效应用,此后喷管流动状态与等面积比单钟形喷管基本没有差异,喷管的比冲随着高度增加而增加。
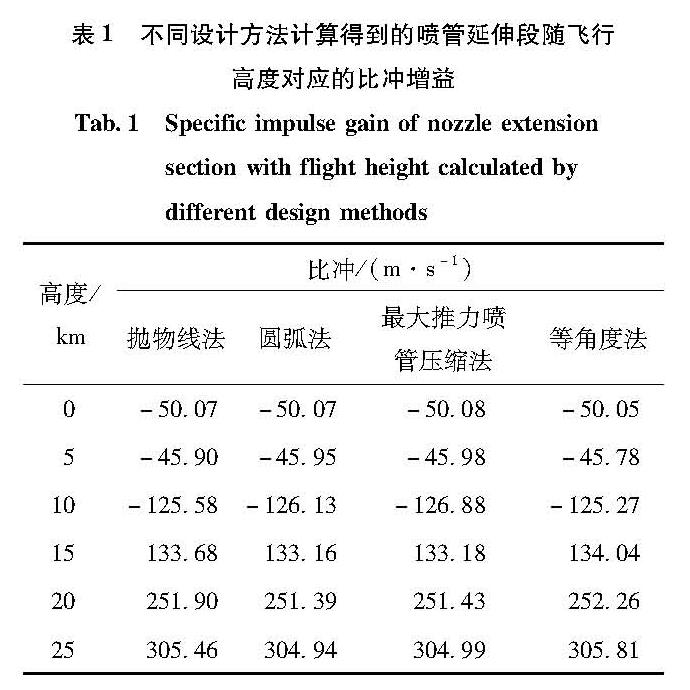
2.5 双钟形喷管性能计算结果分析表1列出了4种方法设计的双钟形喷管延伸段的比冲随高度变化情况。可以看出,在地面0 km和低空5 km高度时,喷管的分离点位于基准喷管出口处,喷管延伸段的内壁面压力略低于环境压力,导致喷管延伸段产生附加阻力,喷管延伸段产生负比冲。
表1 不同设计方法计算得到的喷管延伸段随飞行高度对应的比冲增益
Tab.1 Specific impulse gain of nozzle extension section with flight height calculated by different design methods在10 km高度时,双钟形喷管已经满流,此时双钟形喷管的壁面压力和设计状态是一致的。但是,在此高度下,喷管出口静压是低于环境压力的,喷管内的超声速气流在喷管出口处产生一道斜激波,经过斜激波后燃气静压恢复至与环境压力基本相同,此时由于双钟形喷管出口压力低于环境压力,会产生额外的比冲损失。
在15 km、20 km以及25 km工作高度时,双钟形喷管处于欠膨胀状态,喷管出口压力高于环境压力,喷管的燃气流出喷管后还要继续膨胀,此时,喷管延伸段会产生额外的比冲增益。
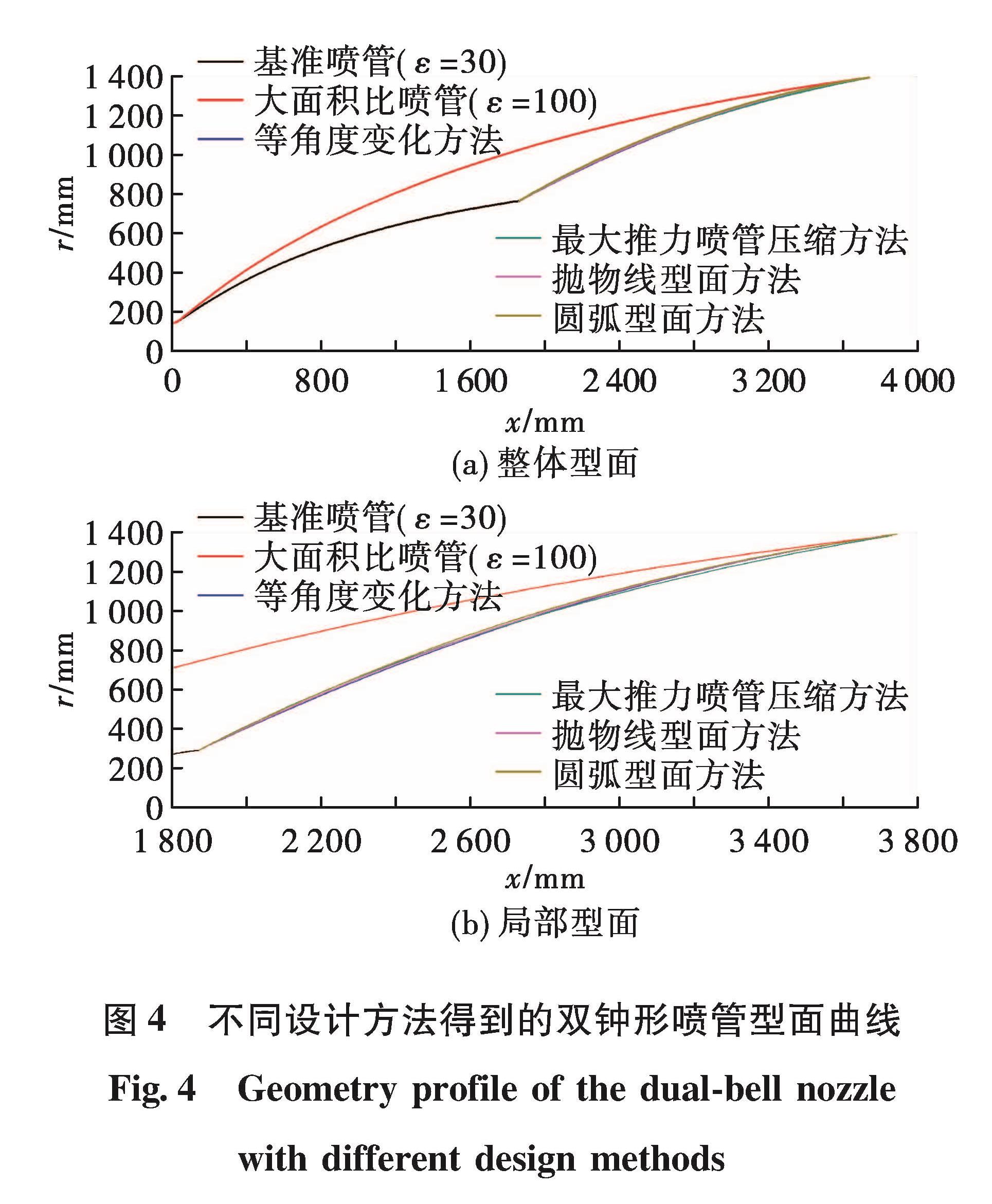
表2列出了4种方法设计的双钟形喷管比冲性能,可以看出,4种方法设计的双钟形喷管比冲相差很小,比冲相差不到1 s。这也表明喷管延伸段采用上述4种方法设计比冲性能差别很小。
2.6 双钟形喷管较最大推力喷管性能对比分析虽然4种方法设计的比冲差别比较小,但是采用轴向等角度变化型面设计的双钟形喷管比冲较其他3种略高一点。因此,本文选用轴向等角度变化这种方法对设计的双钟形喷管进行了全高度流场仿真分析,获得了比冲性能,并与采用基准喷管的全高度比冲进行了对比分析。
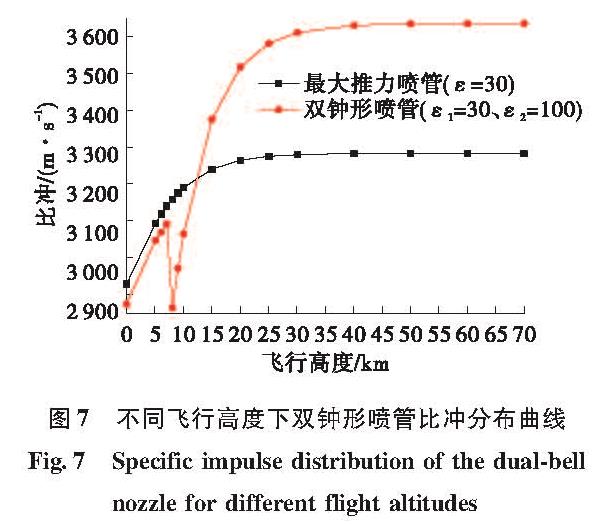
图7给出了双钟形喷管在不同飞行高度下的比冲曲线,其中,黑色是基准喷管的比冲曲线,可以看出,从海平面到6 km高度左右时,由于喷管延伸段的附加阻力损失,导致双钟形喷管的比冲比基准喷管的比冲低一些,平均低约1.5%左右。
在飞行高度7 km到12 km之间,双钟形喷管的主流完全附着于喷管延伸段,双钟形喷管处于满流状态,但是由于双钟形喷管出口压力低于环境压力,导致双钟形喷管比冲比基准喷管要低,在8 km高度双钟形喷管比冲较基准喷管比冲相差达到极值,最大相差约9.28%。
随着飞行高度的增加,喷管出口的环境压力不断减小,喷管的比冲不断增加,从12 km左右开始,双钟形喷管的比冲高于基准喷管的比冲,到50 km后,双钟形喷管的比冲比基准喷管比冲高约10.69%。
3 结论
通过对室压8.5 MPa,基准喷管面积比为30,喷管总面积比100的双钟形喷管进行设计和性能分析,可以得出以下结论:
1)喷管延伸段采用抛物线法、圆弧法、最大推力喷管型面压缩法以及等角度法4种方法设计的双钟形喷管比冲性能相差小于1 m/s,等角度法在4种设计方法中比冲性能最高。
2)从海平面到6 km高度左右时,由于喷管延伸段会产生附加阻力损失,双钟形喷管的比冲比基准喷管的比冲平均低约1.5%左右。
3)在飞行高度7 km到12 km之间,双钟形喷管处于满流状态,由于双钟形喷管出口压力低于环境压力,使得双钟形喷管比冲低于基准喷管,在8 km高度双钟形喷管比冲比基准喷管比冲低约9.28%,达到极大值。
4)随着飞行高度的增加,双钟形喷管出口的压力不变,而环境压力不断减小,从12 km左右开始,双钟形喷管的比冲高于基准喷管的比冲,到50 km后,双钟形喷管的比冲比基准喷管比冲高约10.69%。
5)通过本文分析结果来看,双钟形喷管延伸段采用不同设计方法对比冲性能影响很小,因此,后续研究双钟形喷管延伸段的设计,建议从双钟形喷管分离点转捩的安全性考虑。
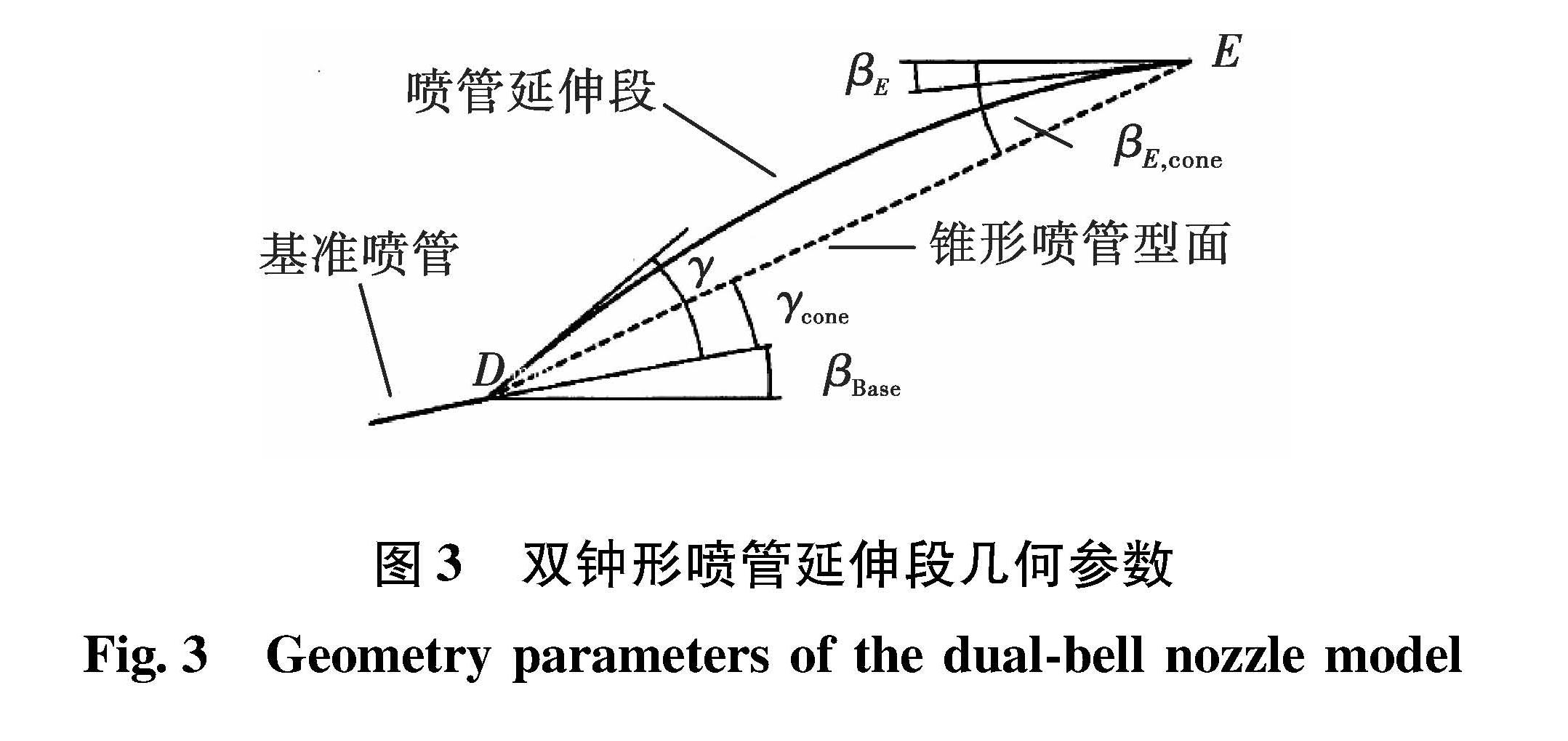
1.1 基准喷管设计方法双钟形喷管的基准喷管一般采用Rao方法设计成最大推力喷管,以获得最大的性能。目前液体火箭发动机基本都是采用这种喷管,其长度是具有相同面积比锥角为15°的锥形喷管长度的75%~85%。然而,这种粗略的近似无法用来给出双钟形喷管的基准喷管的准确长度。基准喷管长度的选择也影响双钟形喷管的结构质量,因此,必须对喷管质量和两种工况下的喷管性能之间作优化选择,以找出基准喷管和喷管延伸段的最佳长度比。
本文设计时,结合目前液体火箭发动机最大推力喷管的设计经验,基准喷管的长度选择为15°锥形喷管长度的80%。
1.2 喷管延伸段设计方法喷管延伸段目前没有一个明确的设计方法和准则,本文在设计时拟考虑采用下面几种方法进行喷管延伸段的型面设计,然后进行仿真分析,获得了不同飞行高度下的喷管性能,最后根据计算获得的喷管性能来分析采用哪种方法设计喷管延伸段最优。
本文拟采用的具体设计方法和过程如下:
1.2.2 确定喷管延伸段的长度借鉴最大推力喷管的设计经验,双钟形喷管的长度选取的是整个喷管面积比对应的15°锥形喷管长度的80%。整个喷管长度确定以后,除掉基准喷管的长度,就是喷管延伸段的长度。
1.2.3 确定喷管延伸段设计方法双钟形喷管的基准喷管面积比和总面积比在设计时是给定的,根据上面所述,延伸段喷管长度和喷管出口角确定后,基准喷管出口的坐标D和喷管延伸段出口的坐标E是已知的,至此,采用不同的方式就可以求得不同的喷管延伸段型线。
1)抛物线型面
最大推力喷管的型面可以用抛物线近似表征,因此,采用抛物线设计喷管型面是一种很常用的方法。根据上面的论述,知道D点和E点的坐标,同时知道E点的角度,根据抛物线方程y=ax2+bx+c,通过式(1)~(3)所示边界条件就可以求解得到抛物线系数,然后得到喷管扩张段的型面坐标。
yD=ax2D+bxD+c(1)
yE=ax2E+bxE+c(2)
tanβE=2axE+b(3)
2)圆弧型面
第二种思路是将喷管延伸段DE设计为圆弧,根据上面的论述,知道D点和E点的坐标,同时知道E点的角度,根据圆弧方程(x-a)2+(y-b)2=r2,通过式(4)~式(6)所示边界条件就可以求解得到圆的系数,然后得到喷管扩张段的型面坐标。
(xD-a)2+(yD-b)2=r2(4)
(xE-a)2+(yE-b)2=r2(5)
tanβE=(dyE)/(dxE)(6)
3)最大推力喷管型线压缩
第三种设计思路是根据最大推力喷管原理,首先采用大面积比设计最大推力喷管型面,然后取基准喷管面积比到大面积比的型线,由于这样的喷管延伸段型面长度比较大,为了和双钟形喷管的长度保持一致,在轴向方向进行等比例压缩得到最终的喷管延伸段型面坐标。
4)轴向等角度变化型面
第四种思路是首先给定D点和E点的角度,然后型面的切角在轴向方向上等角度减小,最终确定出喷管延伸段型面。
- [1] GÉNIN C,GERNOTH A,STARK R. Experimental and numerical study of heat flux in dual bell nozzles[C]//47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. San Diego,California. Reston,Virginia:AIAA,2011:5613.
- [2] HORN M,FISHER S.Dual-bell altitude compensating nozzles[R].NASA-CR-194719,1994.
- [3] VERMA S B,STARK R,NUERENBERGER-GENIN C,et al.Cold-gas experiments to study the flow separation characteristics of a dual-bell nozzle during its transition modes[J].Shock Waves,2010,20(3):191-203.
- [4] VERMA S B,STARK R,HAIDN O. Effect of ambient pressure fluctuations on dual-bell transition behavior[J].Journal of Propulsion and Power,2014,30(5):1192-1198.
- [5] NÜRNBERGER-GENIN C,STARK R. Flow transition in dual bell nozzles[J].Shock Waves,2009,19(3):265-270.
- [6] NASUTI F,ONOFRI M,MARTELLI E. Role of wall shape on the transition in axisymmetric dual-bell nozzles[J].Journal of Propulsion and Power,2005,21(2):243-250.
- [7] NASUTI F,ONOFRI M,MARTELLI E. Role of wall shape on the transition in axisymmetric dual-bell nozzles[J].Journal of Propulsion and Power,2005,21(2):243-250.
- [8] PONOMARYOV N,VOINOV A,DUMNOV G,et al.Dual bell nozzles for rocket engines of launch vehicle upper stages and orbitral transfer vehicles[C]//33rd Joint Propulsion Conference and Exhibit. Seattle,WA. Reston,Virginia:AIAA,1997:3089.
- [9] MIYAZAWA M,TAKEUCHI S. Propulsion and flight performance evaluation of dual-bell nozzles[C]//AIAA/AAAF 11th International Space Planes and Hypersonic Systems and Technologies Conference. Orleans,France. Reston,Virginia:AIAA,2002:5233.
- [10] MIYAZAWA M,TAKEUCHI S,TAKAHASHI M. Flight performance of dual-bell nozzles[C]//40th AIAA Aerospace Sciences Meeting & Exhibit. Reno,NV. Reston,Virginia:AIAA,2002:686.
- [11] KBAB H,SELLAM M,HAMITOUCHE T,et al.Design and performance evaluation of a dual bell nozzle[J].Acta Astronautica,2017,130:52-59.
- [12] STARK R,GÉNIN C,MADER C,et al.Design of a film cooled dual-bell nozzle[J].Acta Astronautica,2019,158:342-350.
- [13] GÉNIN C,GERNOTH A,STARK R. Experimental and numerical study of heat flux in dual bell nozzles[J].Journal of Propulsion and Power,2012,29(1):21-26.
- [14] HAGEMANN G,FREY M,MANSKI D,et al.A critical assessment of dual-bell nozzles[C]//33rd Joint Propulsion Conference and Exhibit. Seattle,WA. Reston,Virginia:AIAA,1997.
- [15] SCHNEIDER D,GÉNIN C,STARK R,et al.Numerical model for nozzle flow application under liquid oxygen/methane hot-flow conditions[J].Journal of Propulsion and Power,2018,34(1):221-233.
- [16] MIYAZAWA M,OTSU H. An analytical study on design and performance of dual-bell nozzles[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno,Nevada. Reston,Virginia:AIAA,2004:380.
- [17] JONES D S,RUF J H,BUI T T,et al.Conceptual design for a dual-bell rocket nozzle system using a NASA F-15 airplane as the flight testbed[C]//50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. Reston,Virginia:AIAA,2014:3956.
- [18] 郑孟伟,朱森元,张扬军. 双钟形喷管流场数值模拟与试验验证[J].导弹与航天运载技术,2005(2):26-30.
- [19] 许晓斌,邓建平,舒海峰,等.高度补偿喷管冷态模拟与推力测量试验技术研究[J].实验流体力学,2007,21(1):82-86.XU X B,DENG J P,SHU H F,et al.The test technique investigation on the cold-jet simulation and propulsion force measurement of altitude-compensated nozzles[J].Journal of Experiments in Fluid Mechanics,2007,21(1):82-86.
- [20] 王一白,覃粒子,刘宇,等.高度补偿喷管的氢氧热试研究[J].航空动力学报,2007,22(2):316-322.
- [21] 洪流. 双钟形喷管的临界评估[J].火箭推进,1998,24(5):17-34.HONG L. Critical evaluation of double bell nozzle [J].Journal of Rocket Propulsion,1998,24(5):17-34.