作者简介:闫松(1988—),男,博士,研究领域为结构动力学模型修正、载荷识别,非接触测试。
(1.西安航天动力研究所 液体火箭发动机技术重点实验室,陕西 西安 710100; 2.航天推进技术研究院,陕西 西安 710100; 3.西安航天动力研究所,陕西 西安 710100)
(1.Science and Technology on Liquid Rocket Engine Laboratory,Xi'an Aerospace Propulsion Institute, Xi'an 710100,China; 2.Academy of Aerospace Propulsion Technology,Xi'an 710100,China; 3. Xi'an Aerospace Propulsion Institute, Xi'an 710100,China)
model updating; liquid rocket engine; static test; modal test; thrust frame
备注
作者简介:闫松(1988—),男,博士,研究领域为结构动力学模型修正、载荷识别,非接触测试。
为了获得准确的液体火箭发动机机架的结构动力学模型,采用精细化的结构动力学建模方法,建立了可以同时反映机架静力和动力学特性的详细有限元模型,并以两种状态下实测数据对机架模型进行了进一步修正。开展了固支状态下的静力试验,获得了机架上关键测点的位移响应; 开展了自由状态下的模态试验,获得了自由状态下机架的固有频率和振型; 最后以静力试验的位移数据和模态试验的固有频率数据为目标函数,对机架各部分材料的弹性模量中关于位移和频率最灵敏的6个参数进行了修正。结果 表明:修正后的机架模型不仅在修正采用的频率范围内与实测值吻合得很好,而且在修正采用的频率范围外理论和试验结果的相关性也有较大提高。模型修正中联合静态响应数据和动力学数据是可行的,静力学试验结果可以提供模态试验中得不到的信息,有利于模型修正过程。
In order to obtain an accurate structural dynamic model of thrust frame in liquid rocket engine,a detailed structural dynamics modeling approach was adopted to establish a detailed finite element(FE)model that can simultaneously describe the static and dynamic characteristics of the frame.The established model was further updated according to two different types of test data. The static test under the fixed support state was carried out,and the displacement response of the key measuring points on the frame was obtained. The modal test under the free state was carried out,and the natural frequency and mode shape under this state were identified. Finally,using the obtained displacement data and the natural frequencies as the objective function,the six most sensitive parameters to displacement and frequency in the elastic modulus of frame materials were updated. The results show that the updated frame model agrees well with the measured values not only within the frequency range used in the correlation,but also beyond the frequency range used in the correlation. It is feasible to combine static response data and modal test data in the model updating. The static test results can provide the information that is not available in the modal test,which is beneficial to the model updating process.
引言
精确的液体火箭发动机结构动力学模型是至关重要的,它是进行发动机界面载荷和传递路径分析的前提。美国20世纪90年代在MC-1发动机上开展了界面载荷研究[1-2],为了获得一个精确的整机结构动力学模型,先后进行了多轮的模型修正[3],并单独开展了高温下复合材料喷管的模态试验用于修正喷管的动力学模型[4]。1976年至1978年,NASA基于SPAR有限元计算程序分别建立了高压燃料泵、高压氧泵和SSME(不包括涡轮泵)的有限元模型用于结构动力学仿真[5]。在随后的几十年,SSME的结构动力学模型逐渐发展完善,2011年时SSME的动力学模型已经用于计算喷管流动分离的侧向力载荷引起的动力学响应[6],该模型较以往的模型更加精细,动力学模型中氧泵和燃料泵可以反映产品的外形,且整机模型包含了较细的管路。
相比于国外,目前国内液体火箭发动机结构动力学模型的精度偏低,模型修正技术在该领域应用匮乏。以机架为例,在对发动机机架的建模中,之前的研究中均采用共节点梁单元对拉杆进行简化,且仅利用整机模态试验结果对整机模型进行修正,而未单独开展机架模态试验修正机架模型,因此也就无法修正机架中不精确的建模参数[7-8]。模型修正技术作为液体动力技术基础研究的一个重要研究方向[9],是提高液体火箭发动机结构动力学模型精度的有效途径。根据修正对象不同,本质上有两种不同的模型修正方法:矩阵型和参数型。矩阵型修正方法[10-11]通过一步计算直接对质量、刚度和阻尼矩阵进行修正,不需要迭代,可以精确地再现试验模态参数; 然而,由于其不考虑具体的物理结构,修正后的质量阵和刚度阵没有任何物理意义,不能和原始有限元参数的变化联系起来,不利于工程应用。参数型修正方法通过逐步修正有限元模型中的物理参数(如材料参数、几何参数、边界条件等)来修正模型,使得修正后模型可以在某种精度下再现试验结果,这种固有特性使得修正后的质量矩阵和刚度矩阵有其物理意义,节点的连通性也能保证。参数型修正方法的修正结果是设计变量或模型假设的误差,这可以给未来再对相似结构进行建模时提供经验。此外,如果修正的模型是用来对未测试的载荷条件或者修改后的结构构型进行预测,通过修正不确定的建模假设而不是修正无物理意义的部分就尤为重要[12]。
目前发动机模型修正遇到的一个问题是待修正的未知参数多,而实际可用的测试信息少,也就是说模型修正存在非唯一解,为了解决模型修正欠定的问题,需要利用大量的试验数据。目前动力学数据如模态参数[13]、频响函数、动力学响应等常作为目标函数对有限元模型进行修正,杨智春等系统总结了动力学模型修正常用的目标函数[14]。Xiao等认为动力学参数如固有频率,给出的是结构的全局响应,对于局部参数不敏感,而静力学参数,如位移和应变,对于测点附近的局部参数更加敏感[15]。Catbas等研究表明当开发一个有效的有限元模型,需要利用不同类型的测量数据[16]。Horta等在对桥梁有限元模型修正时,首先通过静态测试数据修正了刚度矩阵,而后通过实测固有频率修正了质量矩阵[17]。Schlune等结合静态试验数据和动力学数据对桥梁的有限元模型进行了修正[18]。
本文以液体火箭发动机机架为例,建立了详细的机架有限元模型,并利用静力试验和模态试验数据对模型进行了修正。静力试验数据用于模型修正时遇到的主要问题是,实际静力学试验很难提供完全刚性的边界条件,而有限元模型很容易提供绝对刚性的边界条件,由此造成实测响应与计算响应差别很大。一种解决办法是建模时采用弹簧单元代替固支边界条件[19],该方法中弹簧的刚度参数也是待修正的不确定量,这必然会造成待修正参数增多。本文采用的方法如下:试验时测量机架与试验基座连接处的实际位移,将该处位移作为强制位移边界条件施加于有限元模型上,进而比较机架上其他测量点的位移,计算结果表明该方法是有效的。激光测振进行自由模态试验的一个主要问题是激振器激励下结构会存在刚体位移,激光测振技术对刚体位移很敏感,为了克服激振时机架的刚体位移,本文采用的方法是用弹簧绳将机架吊起,机架下端一个角与海绵垫轻微接触,这种方法可以很好地抑制刚体位移而不影响机架的弹性模态。
1 静力试验
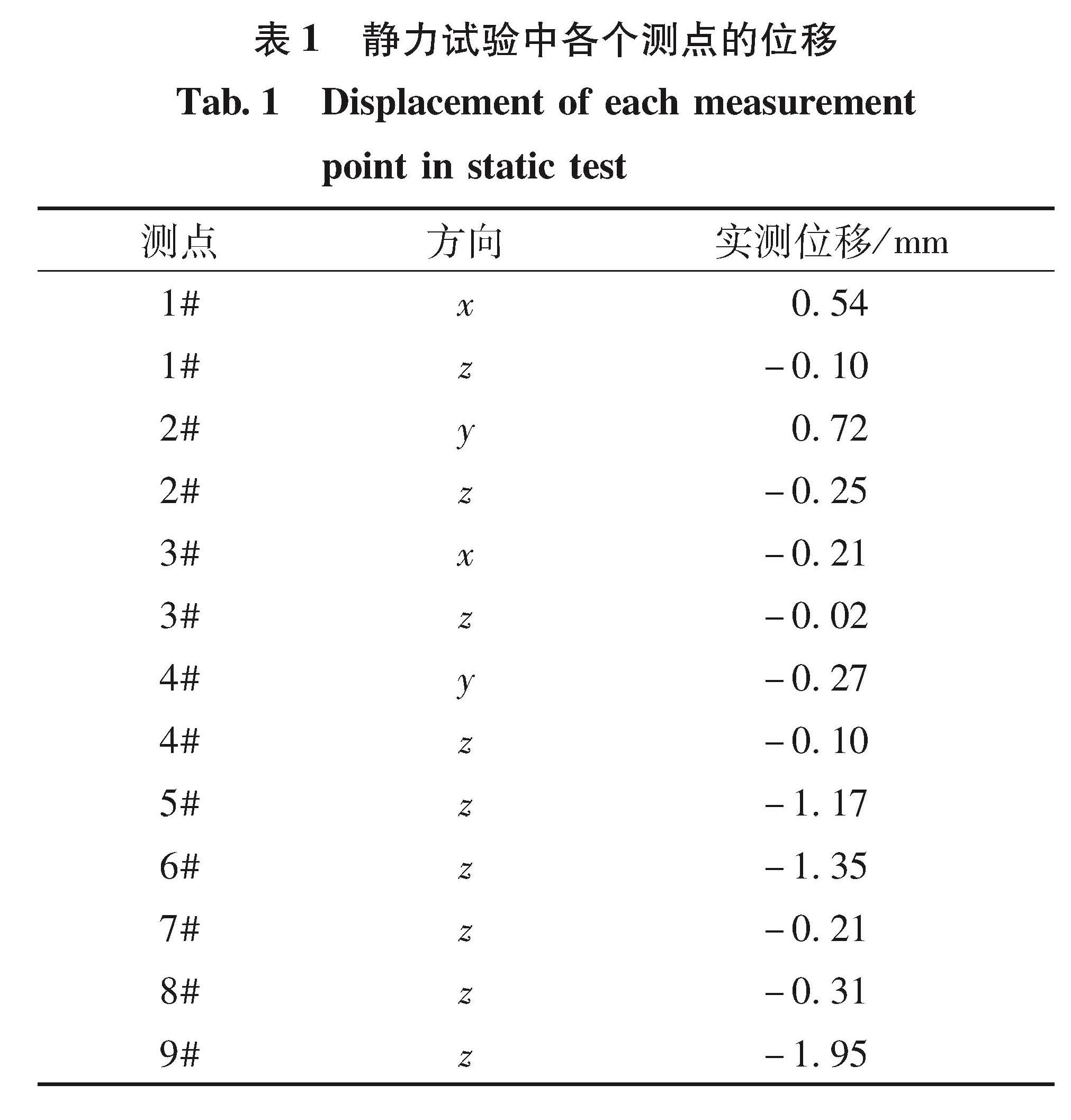
静力试验模拟真实工作情况下机架受力情况,如图 1所示,机架底面对角线长2 200 mm,高度770 mm。两伺服机构力F加载至21 kN后,逐步加载推力R至120 kN,伺服机构力作用于伺服机构支耳,推力作用于机架中心。机架底部1#、2#、3#、4#位置处采用螺栓固定于试验基座上。共安装17个位移传感器,分别记录测点1#~9#的z向位移,1#、3#、5#、7#的x向位移,2#、4#、6#、8#的y向位移。
静力试验得到的各个测点位移如表 1所示,从表中可以看出1#、2#、3#和4#测点的位移不为零,表明在静力加载下,试验基座发生了变形,试验基座不能提供绝对刚性的边界条件。机架中心9#测点的z向位移最大,为1.95 mm,其次伺服机构力作用点附近5#和6#测点的z向位移较大,分别为1.17 mm和1.35 mm。
2 模态试验
由于实验室中难以提供绝对刚性的固定支撑,相对而言,自由边界更容易获得。因此对于机架,开展了自由状态下的模态试验。为了模拟自由边界条件,机架用弹性绳吊起,下端一角与海绵垫轻微接触以限制刚体位移,如图 2所示。由于机架中的承力杆多数是倾斜的且表面是弧面,传统的振动传感器难以进行精确的空间和轴向定位,因此本文采用三维扫描测振技术[20]开展模态试验,微型激振器施加激励,测试发现激励力采用Burst chirp信号可以获得较好的信噪比。测试在夜间进行,此时实验室的噪声干扰最小。
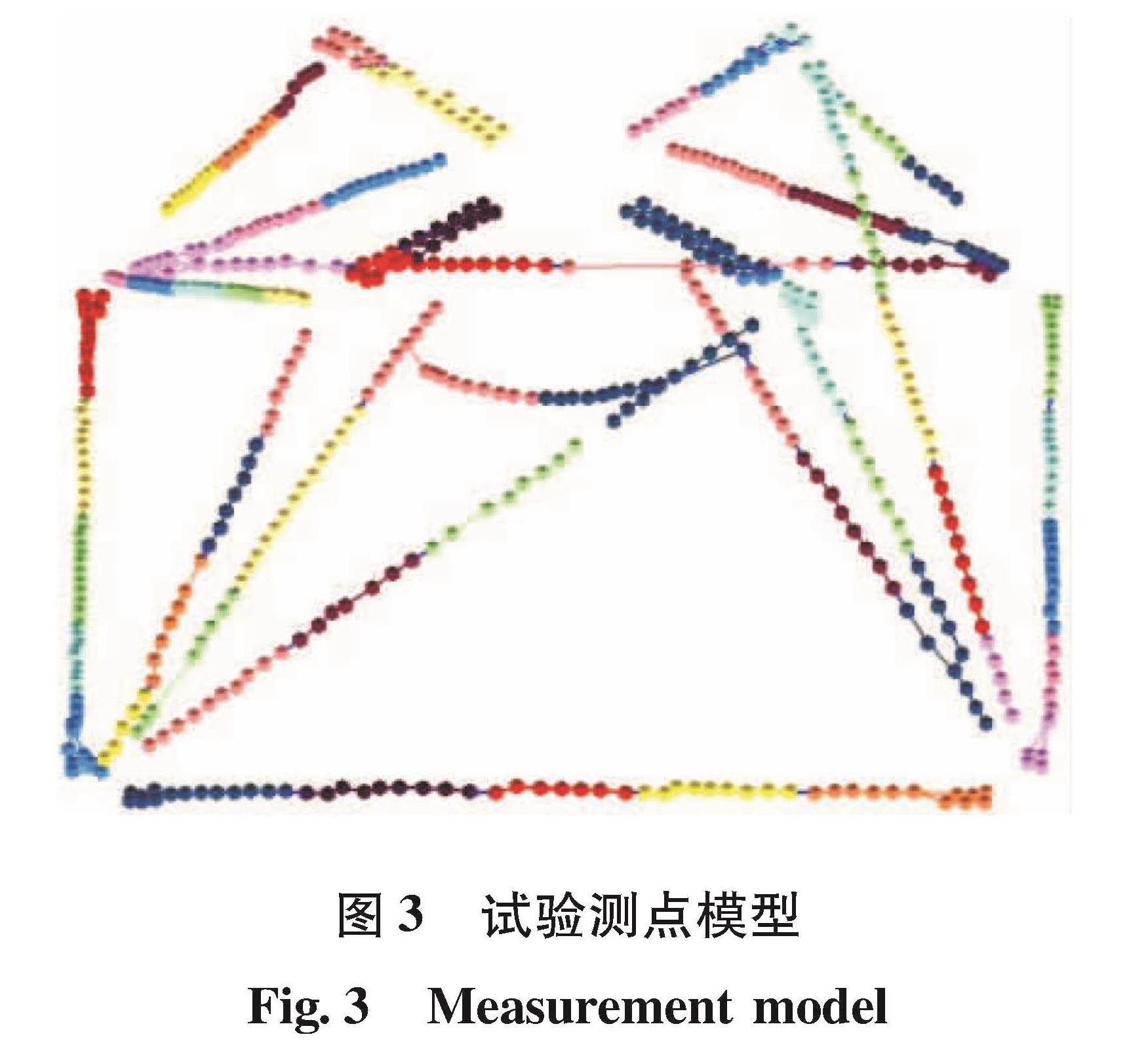
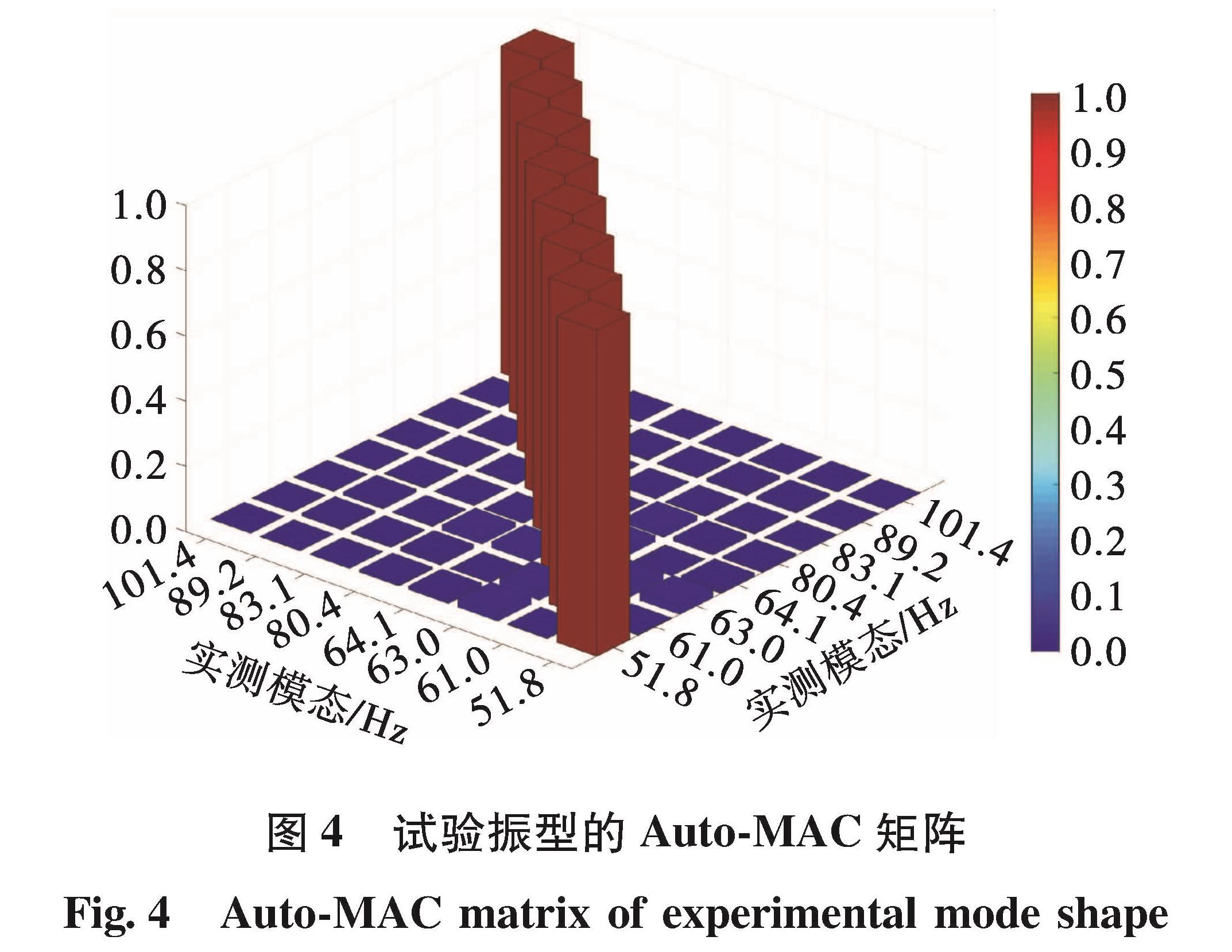
如图3所示,整个测试模型中共包含632个测点,可以获得精细的各阶振型。首先获得机架各个响应测点相对于激励点的频响函数,而后将频响函数数据导入LMS.test.lab进行振型拟合。机架的前9阶固有频率分别为43.1、51.8、61.0、63.0、64.1、80.4、83.1、89.2、101.4 Hz。受激励点位置影响,三维扫描测振模态试验中机架的第1阶模态未激发,本文中给出的第1阶固有频率及振型是采用传统粘贴振动传感器的模态测试方法获得。第2~9阶实测振型的Auto-MAC矩阵如图 4所示,其中非对角元素最大值为0.024 9,表明各阶振型良好的正交性。
第1~9阶实测振型如图 5所示,从图中可以看出,三维扫描测振技术可以获得精细的实测振型,清楚分辨各个承力杆的变形,这为后续进行理论/试验相关性分析提供基础。
3 模型修正过程
3.1 初始模型经过3轮的手工修改,最终建立的初始有限元模型如图 6所示,共32 747个单元和37 665个节点。不同的颜色表示不同的属性,整个模型包括32个不同属性。建立的有限元模型质量比实际机架质量略小,差别为1.5%,误差主要来源于实际机架焊接造成的质量增加。
建模时采用精细化的建模策略,尽量反映真实结构特征,图 7给出了同一坐标系下的有限元模型与试验模型,试验中的测点位于杆的表面,而有限元模型的梁单元位于杆的中心,因此试验测点和有限元节点会偏离一定的距离。搜索距离试验测点最近的有限元测点进行配对,632个试验测点全部与有限元节点一一对应。
图7 同一坐标系下机架的试验模型及有限元模型
Fig.7 Experimental model and FE model of thrust frame under the same coordinate system图8给出了初始模型理论和实测振型的MAC矩阵,从图中可以看出,有7阶理论与实测结果吻合得很好,有限元49.6、59.4、60.3、77.7、79.9、87.2、94.8 Hz与对应实测振型的MAC值分别为0.985、0.931、0.925、0.985、0.972、0.935和0.869。有2阶理论和实测结果相关性较差,57.8 Hz与对应61.0 Hz实测振型的MAC值为0.565、58.3 Hz理论振型无对应的实测振型,原因可能是由于试验中所选激励方向没能激发该阶模态。
由表 1可知,静力试验时1#、2#、3#、4#测点的位移不为零,即试验基座不能提供完全刚性的边界条件。而在有限元模型上如果对1#、2#、3#、4#测点施加固支边界条件,将会造成整个模型中的位移响应与实测位移响应有较大差别。本文将实测的1#、2#、3#、4#的位移作为强制位移边界条件,施加于有限元模型,比较实测和计算的5#、6#、7#、8#和9#测点的位移。图 9为静力载荷下机架变形的位移云图,表 2为初始模型理论与实测位移的对比,8#测点的误差最大,为-12.9%,9#测点误差最小,为0.51%,其余3个测点误差在5%左右,说明建立的有限元模型能有效反映结构静力学特性。由此,通过精细化建模,我们认为得到了一个合适的初始模型,后续在此模型基础上开展自动的模型修正。
3.2 灵敏度分析由于有限元模型是根据机架CAD模型建立,且机架几何结构简单,上下均有空间位置精确的定位孔,可以认为机架不存在加工尺寸偏差,模型中机架的各部分质量与实际产品质量相同,模型中不确定参数为各部分的弹性模量。整个模型包括32个不同的属性,分析了5#~9#测点z向位移和前3阶固有频率对32个弹性模量的灵敏度,分别如图 10和图 11所示。
图 10 5#~9#测点z向位移对32个弹性模量的灵敏度
Fig.10 Sensitivity of 5#~9# z direction displacement to 32 elasticity moduli由图 10可知,对位移最灵敏的5个设计参数编号为22、21、14、9、29,由图 11可知,对于频率最灵敏的3个设计参数编号为4、14、22。综合两者考虑选取参数4、9、14、21、22、29为6个待修正的参数。图 12给出了这6个参数在机架中的位置。
3.3 目标函数目标函数即是理论与试验结果的差别,一般应包含尽可能多的数据,以确定待修正参数。模型修正的过程即是不断地调整待修正参数的值使得目标函数值最小。本文目标函数包含位移残差和固有频率残差两项,其中位移残差定义如下
fd(p)=∑i[wd((udi(p)-u-di)/(u-dmax))]2(1)
式中:p是待修正的参数,本文中即是6个最灵敏的设计参数:udi(p)是有限元计算所得i#测点的位移; u-di是试验测得i#测点的位移; u-dmax是试验测得的最大位移,选取实测5#、6#、7#、8#和9#测点的z向位移作为修正目标; wd是静态位移残差的权重。
固有频率残差定义如下
ff(p)=∑j[wf((fj(p)-f-j)/(f-j))]2(2)
式中:fj(p)是有限元计算所得的固有频率; f-j是与之对应的实测固有频率,选取前3阶固有频率作为修正目标; wf是固有频率残差的权重。合理选择wd和wf这两个值可以获得很好的收敛效果,且避免目标函数中的某一项统治优化过程。本文中选择wd=wf=1。
最终模型修正的目标函数定义为
f(p)=ff(p)+fd(p)(3)
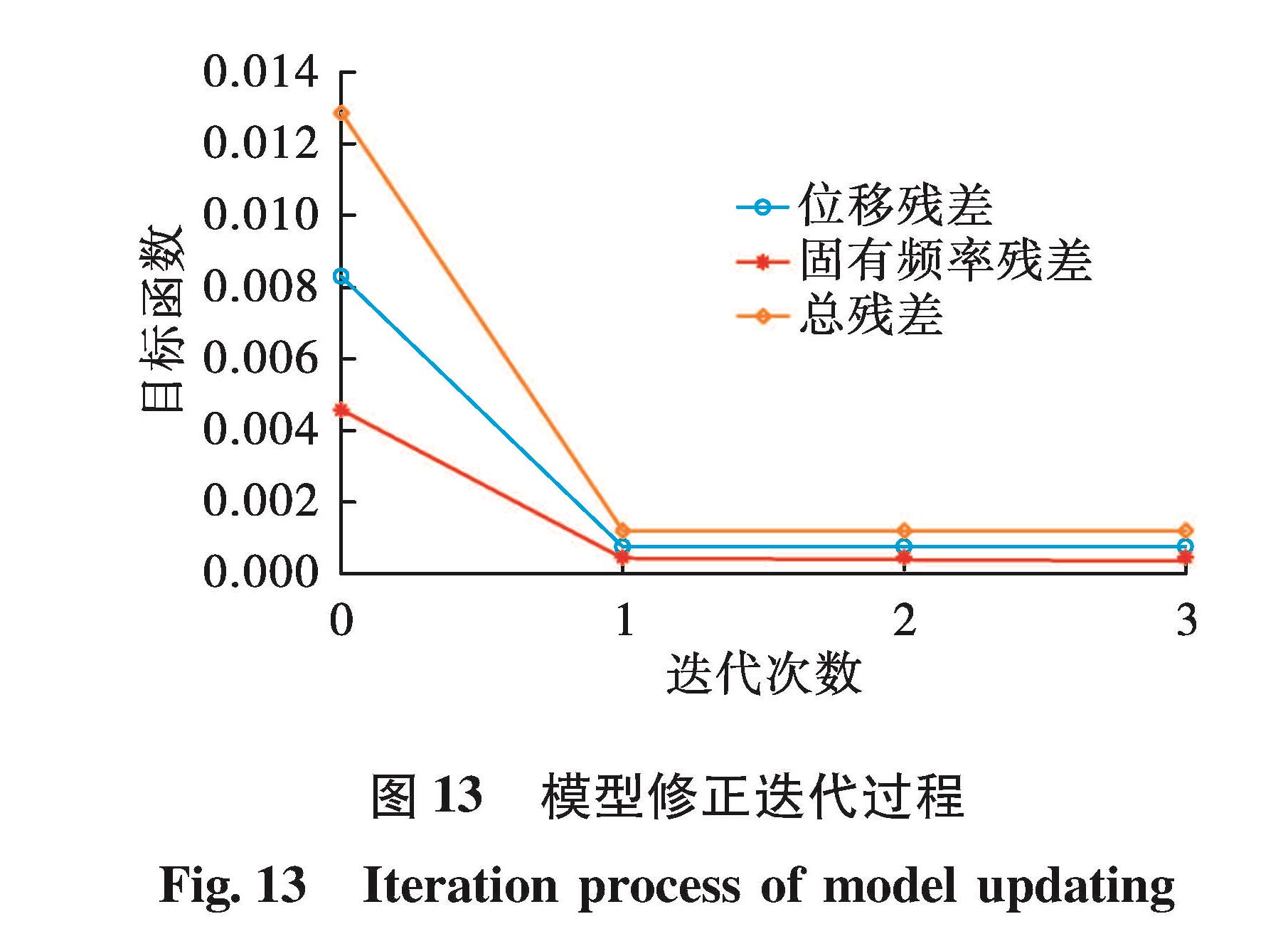
3.4 修正结果采用基于灵敏度的SQP算法进行模型修正,它的优点是收敛速度快,如图 13所示,经过3次迭代,目标函数收敛。位移残差从8.3×10-3下降到7.2×10-4,固有频率残差从4.6×10-3下降到3.4×10-4。
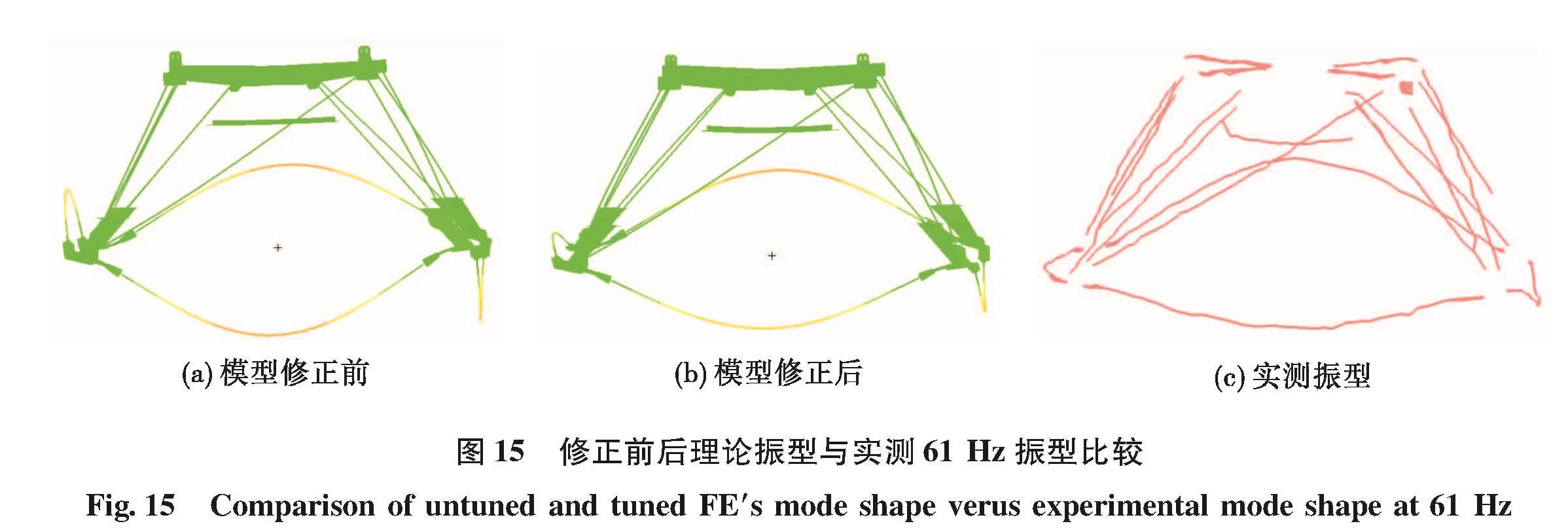
图 14给出了模型修正后理论与试验振型的MAC矩阵,表3给出了修正前后理论与试验结果的对比,可以看出:①修正后前9阶理论与实测固有频率最大误差仅为-2.54%,第10阶误差为-5.52%; ②除第3阶和第10阶外,其余各阶理论和实测振型的MAC值均在0.950以上,第3阶MAC值由修正前的0.565提高到修正后的0.821,图 15给出了第3阶振型修正前后理论与实测振型的对比,直观上看,修正后第3阶振型与实测结果吻合得更好; ③虽然目标函数中只包含了前3阶固有频率,但考察第5~10阶理论与实测结果的相关性,固有频率误差有5个有较大幅度降低,1个修正前后无变化,MAC值有6阶升高,1阶无变化,1阶降低。模型修正成功的一个标志即是能有效预测不在修正所使用频率范围内的结构特性[21]。图 16给出了修正后各阶理论振型,与图 5对比,理论和实测振型高度一致。
图 15 修正前后理论振型与实测61 Hz振型比较
Fig.15 Comparison of untuned and tuned FE's mode shape verus experimental mode shape at 61 Hz表4给出了模型修正前后5个位移测点理论与实测值对比,可以看出,9#测点与实测值吻合得极好,误差仅为-0.51%,且修正前后无变化,其余4个测点修正后与实测值的误差有较大程度的降低。由此可知,通过精细化建模和模型修正,得到了一个可以同时反映机架静力学和动力学特性的有限元模型。
4 结论
以机架为例验证了结构动力学精细化建模技术,通过联合固支状态下静力试验数据和自由状态下的模态试验数据,对机架模型进一步修正,最终建立了一个可以同时反映机架静力学和动力学特性的有限元模型。主要结论如下:
1)联合静力和动力试验数据进行模型修正是可行的,修正后的模型不仅在修正频率内与试验结果更加吻合,而且在修正频率外与试验结果的相关性也大大提高。
2)相比于传统的模态测试技术,三维扫描测振技术可以获得精细的实测模态振型,使得可以进行高阶振型理论和实测结果的比较,理论和试验振型的MAC值可达0.95以上。
3)将机架与试验基座对接处的实测位移作为强制位移边界条件施加于有限元模型,进而比较其他测点的静态位移是可行的。
- [1] FRADY G,JENNINGS J,MIMS K,et al.Engine system loads analysis compared to hot-fire data[C]//43rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Denver,Colorado.Reston,Virginia:AIAA,2002:1510.
- [2] CHRISTENSEN E,BROWN A,FRADY G. Calculation of dynamic loads due to random vibration environemnts in rocket engine systems[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference. Honolulu,Hawaii. Reston,Virginia:AIAA,2007:1784.
- [3] CHRISTENSEN E,FRADY G,MIMS K,et al.Structural dynamic analysis of the X-34 rocket engine[C]//39th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference and Exhibit. Long Beach,CA. Reston,Virginia:AIAA,1998:2012.
- [4] BROWN A M. Temperature-dependent modal test/analysis correlation of X-34 FASTRAC composite rocket nozzle[J].Journal of Propulsion and Power,2002,18(2):284-288.
- [5] MULLER G R.Finite element models of the space shuttle main engine[R].NASA TM-78260,1980.
- [6] BAKER M,PRAY C. Understanding critical dynamic loads for nozzle and nozzle extension design[C]//47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. San Diego,California. Reston,Virginia:AIAA,2011:5686.
- [7] 杜飞平,谭永华,陈建华. 基于子结构试验建模综合的火箭发动机结构动力分析[J].推进技术,2015,36(10):1547-1553.
- [8] 叶莺樱.某新型发动机结构振动特性分析[D].北京:中国运载火箭技术研究院,2019.
- [9] 李斌.构建基础研究平台,推动液体动力技术创新发展[J].火箭推进,2014,40(1):1-9.LI B. Establishment of fundamental research platform for promoting innovative development of liquid propulsion technology[J].Journal of Rocket Propulsion,2014,40(1):1-9.
- [10] BERMAN A,NAGY E J.Improvement of a large analytical model using test data[J].AIAA Journal,1983,21(8):1168-1173.
- [11] MOTTERSHEAD J E,FRISWELL M I.Model updating in structural dynamics:a survey[J].Journal of Sound and Vibration,1993,167(2):347-375.
- [12] MARWALA T,SIBISI S.Finite element model updating using Bayesian framework and modal properties[J].Journal of Aircraft,2005,42(1):275-278.
- [13] 张安平,陈国平.基于混合人工鱼群算法的结构有限元模型修正[J].航空学报,2010,31(5):940-945.
- [14] 杨智春,王乐,李斌,等.结构动力学有限元模型修正的目标函数及算法[J].应用力学学报,2009,26(2):288-296.
- [15] XIAO F,HULSEY J L,CHEN G S.Multi-direction bridge model updating using static and dynamic measurement[J].Applied Physics Research,2015,7(1):47.
- [16] CATBAS F N,CILOGLU S K,HASANCEBI O,et al.Limitations in structural identification of large constructed structures[J].Journal of Structural Engineering,2007,133(8):1051-1066.
- [17] HORTA L G,REAVES M C,LDW J S.A procedure for static and dynamic model update of finite element models:application to an inflated/rigidized torus[C]//Proceeding of the IMAC XXIV:Conference and Exposition on Structural Dynamic.St Louis,Missouri:[s.n.],2006.
- [18] SCHLUNE H,PLOS M,GYLLTOFT K.Improved bridge evaluation through finite element model updating using static and dynamic measurements[J].Engineering Structures,2009,31(7):1477-1485.
- [19] SOLÍS M,HE L,LOMBAERT G,et al.Finite element model updating of a footbridge based on static and dynamic measurements[C]//Proceedings of the 4th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering(COMPDYN 2013).Kos Island,Greece.Athens:Institute of Structural Analysis and Antiseismic Research School of Civil Engineering National Technical University of Athens(NTUA)Greece,2014.
- [20] 闫松,李斌,李斌潮,等.三维扫描测振技术在液体火箭发动机模态试验中的应用[J].宇航学报,2017,38(1):97-103.