基金项目:高校联合创新基金(CALT20190103)
作者简介:余家泉(1990—),男,硕士,工程师,研究领域为飞行器总体设计。
(中国运载火箭技术研究院,北京100076)
(China Academy of Launch Vehicle Technology,Beijing 100076,China)
air-launched; glide ballistic vehicle; sequential quadratic programming method; solid rocket motor; thrust type
为研究空射滑翔式弹道飞行器固体火箭发动机特性对飞行器综合性能的影响,构建了基于序列二次优化法(SQP)的弹道优化模型,设计了多套不同推力形式、不同特性参数的固体火箭发动机方案。通过开展空射滑翔式弹道飞行器弹道仿真分析,获取了不同动力特性下的最优爬升攻角变化规律,对比分析了相关弹道特征指标。结果 表明:采用长时间-小推力的推力形式,能够增加飞行器弹道顶点速度和射程能力; 采用多脉冲或单室-双推力的推力形式,能够减小飞行器飞行动压,对降低飞行器承载及防热结构质量十分有利。
In order to investigate the effects of solid rocket motor(SRM)characteristics to the comprehensive performance of the air-launched glide ballistic vehicle,a ballistic optimization model based on sequential quadratic programming(SQP)method was constructed,and several SRM schemes with different thrust types and different parameters were designed.By the ballistic simulation analysis of air-launched glide ballistic vehicle,the optimum climbing attack angle variation laws under different SRM characteristics were obtained,and the key ballistic indicators were contrasted.It is found that vehicle has larger ballistic apex velocity and longer range with the thrust mode of long time-low thrust; and the max flight dynamic pressure is lower with dual-pulse or single-chamber double-thrust thrust type,which is beneficial to reduce the weight of load bearing structure and thermal protection structure.
随着现代军事技术的不断发展,战术导弹在局部战争中占据着重要地位,临近空间滑翔式弹道导弹以其优越的机动性能、突防性能成为当前各军事大国研究的重点方向之一[1-4]。由于轰炸机、歼击机等空中平台具有作战灵活性高、空域速域宽等特点,采用空基平台发射滑翔式弹道导弹能够极大提升导弹作战效能,增强空基平台防区外作战能力及作战半径。俄罗斯在2018年对外发布了“匕首”高超声速空面导弹,其搭载米格-31平台发射,采用助推滑翔弹道体制,射程能力可达2 000 km,极大提升了俄罗斯空军作战能力[5]。美国也已在2020年采用 B-52 轰炸机完成了 “空射快速响应武器(ARRW)”作战型“AGM-183”导弹的最后一次系挂试飞,即将具备转向实战化能力[6]。
目前,关于空射弹道导弹或飞行器的技术研究主要集中在空中发射关键技术及弹道优化方面。辛朝军等对空中发射现状、趋势及关键技术进行了全面分析及总结[7]。聂川义等针对空射弹道导弹水平发射特点提出了助推段弹道设计及优化方法[8]。孙丕忠等提出了一种水平发射有翼固体运载火箭的飞行程序角工程设计方法[9]。杨明等提出了基于改进粒子群算法的空射飞行器的助推段弹道规划方法[10]。在能量一定的前提下,发动机的推力形式、工作时间对飞行器的射程能力、载荷及防热设计具有较大影响,在飞行器论证初期,有必要结合总体需求、弹道特点对发动机推力特性进行优化调整,目前该类研究文献较少,需要开展相关研究。
本文针对单级不分离空射滑翔式弹道飞行器特点,建立了多约束弹道优化模型,并分析了不同动力特性对飞行器综合性能的影响,对工程设计具有一定指导意义。
对于单级不分离空射滑翔式弹道飞行器,其飞行弹道一般可分为投放段、助推段、惯性飞行段和机动飞行段。为保证载机平台安全,投放段主要依靠空气舵实现飞行器姿态稳定控制; 当飞行器离开载机一段距离后,固体火箭发动机点火助推,并依靠大攻角实现弹道快速拉起; 发动机工作结束后,飞行器依靠惯性继续爬升,到达预定高度后开始机动飞行; 机动飞行段通常可采用最佳升阻比攻角滑翔以实现最大射程。由于空射飞行器采用了水平发射方式,相较于传统地面垂直发射,飞行器在助推段需要更大的法向过载以实现弹道快速拉起,典型弹道飞行剖面见图1。
忽略地球自转及非球形摄动影响,飞行器在纵平面质点运动方程为[11]
m(dv)/(dt)=Fcos α-CxpS-mgsin θ(1)
mv(dθ)/(dt)=Fsin α+CypS-mgcos θ(2)
(dL)/(dt)=vcos α(3)
(dh)/(dt)=vsin α(4)
(dm)/(dt)=-mc(5)
式中:v为飞行速度; θ为弹道倾角; L为飞行器射程; h为飞行高度; m为飞行器质量; F为发动机推力; α为飞行攻角; g为当地重力加速度; Cx(Ma,α)、Cy(Ma,α)分别为气动阻力系数和升力系数; p为动压; S为参考面积; mc为发动机质量流率。
滑翔式弹道飞行器的主动段一般采用方案弹道,利用俯仰角进行控制,其计算式为
=θ+α(6)
由于俯仰角和气动系数Cx、Cy均与攻角α相关,因此在初步弹道设计时可将攻角α作为优化参量。
考虑固体火箭发动机喷管设计状态及飞行高度变化,推力可以表示为
F=m·cIsp+(pe-pa)Ae(7)
其中
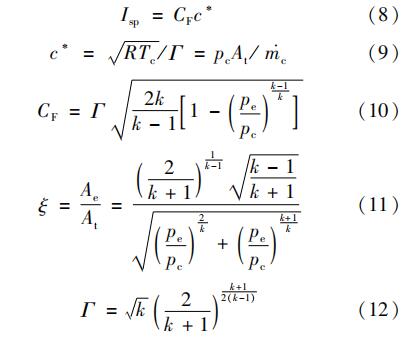 (12)
(12)
式中:m·c为发动机质量流率; Isp为发动机比冲; CF为推力系数; c*为特征速度; k为燃气比热比; R为气体常数; Tc为燃烧室温度; pc为燃烧室压强; pe为喷管出口压强; pa为外界环境压强; Ae为喷管出口面积; At为喷管喉部面积; ξ为喷管扩张比。
c*表征了推进剂的燃烧性能,复合推进剂的特征速度一般为1 500~1 800 m/s; CF表征了喷管的膨胀性能,喷管扩张比ξ越大,表征燃气膨胀越充分,推力系数CF也就越大。
以总冲不变为原则,研究不同发动机推力形式、推力参数对弹道特性影响。将弹道最高点能量作为目标函数,助推段、惯性飞行段攻角作为控制变量,构建优化模型。
目标函数表示为
J=-(vtop2/2+ghtop)(13)
式中vtop、htop分别为弹道最高点速度和最高点高度。
将时间区间划分为N等份,有
t~=(t1,t2,t3,…,tN)T(14)
按照时间区间将控制变量α进行线性化离散,离散后有
α~=(αt1,αt2,αt3,…,αtN)T(15)
考虑弹体结构承载及防热、发动机过载烧蚀、姿态稳定控制等影响,飞行过程中的约束条件主要包括:
1)攻角约束
αmin≤α≤αmax(16)
2)攻角变化率约束
αmin·≤α·≤αmax·(17)
3)动压约束
p=1/2ρv2≤pmax(18)
4)动压攻角乘积约束
|pα|≤Qmax(19)
5)法向过载约束
ny=(Fsin α+Cyps)/(mg)≤nymax(20)
6)法向过载积分约束
∫t </sub>2t1ny≤Ntmax(21)
7)高度约束
htop≤hmax(22)
针对上述多变量非线性优化问题,本文采用序列二次优化法(SQP)[12-13]进行求解。SQP方法的基本思路是将复杂问题转化为目标点附近多个二次规划子问题进行求解,然后更新迭代搜索方向继续寻优,直至逼近最优解。
二次规划子问题可表示为
 (23)
(23)
式中:
 为梯度; dα~为增量; Lα~α~(dα~,λ)为Hessian矩阵,可通过BFGS[14]方法求得; gi(α~)、hj(α~)分别为等式、不等式约束条件。
为梯度; dα~为增量; Lα~α~(dα~,λ)为Hessian矩阵,可通过BFGS[14]方法求得; gi(α~)、hj(α~)分别为等式、不等式约束条件。
基本计算过程如下:
1)获取初始点α~k附近满足式(23)的搜索方向dα~k;
2)采用罚函数P(α~,λ)对搜索步长λk进行优化,得到满足min P(α~k+λ·dα~k,r)条件的最优解λk。P(α~,λ)表示为
P(α~,λ)=J(α~)+∑ni=1ri|gi(α~)|+∑mj=1rj|hj(α~)|(24)
式中ri、rj为罚因子。
3)更新α~k+1=α~k+λ·dα~k,并返回求解式(23),重复上述迭代计算直至dα~满足计算精度要求。
固体火箭发动机通常通过调节推力形式进行能量管理[15-20],常用的推力形式主要包括单推力、单室双推力和多脉冲3种,见图2。
本文采用类似“匕首”的单级不分离导弹为算例,规模上进行一定缩比。飞行器长度7 m,直径0.6 m,质量2 000 kg,推进剂质量1 100 kg,飞行器投放高度10 km,投放速度0.8 Ma。
开展单推力、多脉冲、单室双推力3种动力形式、不同推力特性参数下的弹道分析。其中,单推力、多脉冲、单室双推力助推段压强按照10 MPa考虑,10 km高度比冲270 s; 单室双推力续航段考虑压强降低,结合式(10)对10 km比冲进行修正。
在总冲一定前提下,分析单推力发动机不同推力-时间特性对飞行器综合性能的影响。发动机燃烧室压强按10 MPa考虑,特征速度c*取1 600 m/s,喷管出口压强按10 km高度设计,根据式(7)~式(12)得到4种不同工作时间下发动机主要性能(见表1)。
对不同发动机状态最高点前飞行弹道进行优化分析,获取典型最优攻角-时间曲线(见图3)。结果表明,在满足约束条件前提下,主动段采用大攻角快速拉起,爬升段以0°攻角爬升,获得的弹道最高点能量最大; 同时,发动机推力越大,所需要的拉攻角时间就越短。
对比不同推力-时间特性下弹道关键指标,具体结果见表2。关机点、最高点速度变化情况见图4,助推段射程-高度曲线见图5。
对比方案1-4与方案1-1结果表明:随着工作时间增加、平均推力减小,飞行器关机点速度减小1.2%,关机点高度增加了20.9%,对应弹道最高点能量增加了2.4%,有利于提高飞行器综合射程能力; 此外,飞行器的最大飞行动压减小了37.9%、动压攻角积减小16.1%、主动段法向过载减小29.0%,有利于系统减重优化。因此,采用单推力方案在保证总冲能力一定前提下,应当尽可能增加发动机工作时间。
目前应用的多脉冲发动机以双脉冲为主,本文主要针对双脉冲推力特性开展研究。以单推力方案1-4为基线,构建不同间隔时间双脉冲发动机方案,具体见表3。
对不同双脉冲推力的飞行弹道进行优化,最优攻角-时间曲线见图6。结果表明,采用Ⅰ脉冲大攻角拉起,间隔段恒定攻角过渡,Ⅱ脉冲小攻角继续拉起的弹道能够实现特定约束下最高点能量最大; 随着脉冲间隔时间的不断增大,Ⅱ脉冲对爬升攻角的需求逐渐增大。
不同双脉冲方案对应的弹道关键指标统计情况见表4。最高点前速度、高度、动压变化情况见图7~图9。
表4仿真结果表明:相比于单推力方案,当脉冲间隔时间为10 s时,双脉冲关机点速度降低1.2%,关机点高度增加13.5%,对应弹道最高点能量基本相当,最大动压降低21.7%,法向过载积分降低7.1%; 当脉冲间隔时间大于10 s,弹道最高点能量最大下降3.0%,最大飞行动压基本不变。因此,选择合适的双脉冲间隔时间,可以在保证能量不损失情况下降低飞行动压,有助于飞行器结构减重设计。
以单推力方案1-4为基线,构建不同推力比下的单室双推力方案,其中续航段考虑工作压强降低对比冲进行修正,具体参数见表5。
对单室-双推动力形式的飞行弹道进行优化,最优攻角-时间曲线见图 10。结果表明,采用助推段大攻角、续航段小攻角、惯性飞行段零攻角的弹道爬升方案能够实现特定约束下最高点能量最大化。
不同推力比单室-双推发动机方案对应的弹道关键指标对比情况见表6。最高点前速度、高度、动压变化情况见图 11~图 13。
表6仿真结果表明:相比于单推力方案,随着单室-双推力两级推力比增加,飞行器关机点速度降低2.1%~4.6%,关机点高度增加19.7%~ 54.3%,最大动压降低20.7%,法向过载积分增加3.8%~13.4%,最高点能量基本维持不变。因此,采用单室双推力方案虽然增加了续航段工作时间,但续航段比冲同步下降,在综合作用并未体现出明显的能量优化特性。
表6 弹道关键参数对比(单室-双推方案)
Tab.6 Comparison of ballistic key parameters(single-chamber double-thrust schemes)
本文围绕空射滑翔式弹道飞行器动力装置特性影响开展研究,构建了单推力、双脉冲、单室-双推力3类动力形式、多种动力参数的固体火箭发动机方案,并引入基于SQP算法的弹道优化模型,针对不同动力参数对弹道特性的影响开展数值仿真分析,得到如下结论:
1)针对单推力发动机方案,当工作时间增加60%,飞行器关机点高度增加20.9%,弹道最高点能量增加2.4%,有利于提高飞行器射程; 对应弹道最大飞行动压减小37.9%、动压攻角积减小16.1%、主动段法向过载减小29.0%。
2)相较于单推力发动机方案,双脉冲发动机引入了能量管控措施,当脉冲间隔时间小于10 s时,弹道最高点能量基本相当,最大动压能够降低21.7%; 当脉冲间隔时间大于10 s,弹道最高点能量下降3.0%,最大飞行动压基本不变。
3)相较于单推力发动机方案,单室-双推力发动机采用大推力拉起、小推力续航的方案,飞行器关机点速度降低2.1%~4.6%,关机点高度增加19.7%~ 54.3%,最大动压降低20.7%,法向过载积分增加3.8%~13.4%,最高点能量基本维持不变。表明单室双推力方案虽然增加了续航段工作时间,但续航段比冲同步下降,在综合作用并未体现出明显的能量优化特性。
4)本文研究结果尚未考虑推进剂燃速对长时间-小推力的限制、多脉冲方案带来的点火结构复杂化、单室双推力方案带来的装填比下降等问题,在实际发动机参数论证过程中需要综合考虑上述因素影响。