转子偏心小扰动时,同心环形密封内产生的流体激励力可用如下密封力模型表示。

式中:F_x和F_y分别为密封在笛卡尔坐标系x、y方向所受的径向流体力; K为密封直接刚度系数; k为交叉刚度系数; C为直接阻尼系数; c为交叉阻尼系数; M为主惯性系数。

目前,针对上述密封动力特性系数的求解方法主要有3种:基于二维整体流动理论(bulk-flow theory)的求解方法、三维CFD准稳态法以及三维CFD瞬态法^[22]。其中整体流动理论基于薄膜假设,其忽略了密封径向速度的变化情况,通过试验结果建立了壁面剪切力与平均流速之间的关系,极大地简化了求解过程。该方法因求解速度快,在一定条件下可获得较为可靠的结果,因此在工程上得到了广泛的应用。三维CFD准稳态法以及瞬态法能够有效模拟真实密封结构,求解精度更高,但其求解时间较长,不便进行转子动力学耦合计算。因此,本文采用修正的二维整体流动理论的求解方法对密封动特性系数进行求解,具体求解方法及求解精度见文献[1]。

为考虑密封耦合效应,基于有限元方法,利用矩阵运算将密封动特性系数整合进转子运动方程中,建立转子—密封耦合系统动力学模型。

经典的转子运动方程为

Mu^¨+Cu^·+Ku=Q(2)

式中:M、C、K分别为转子的质量矩阵、阻尼矩阵、刚度矩阵; Q为转子所受的外载荷向量; u=[x₁, y₁,θ_x1, θ_y1, x₂, y₂, θ_x2, θ_y2,…,x_n, y_n, θ_xn, θ_yn]^T为广义坐标,对于n个节点的转子,具有4n个自由度。

可以看出,式(1)所示的密封流体力模型与转子运动方程具有相似的结构。对此,可引入2×4n阶转换矩阵T_j,使该转换矩阵第1行第4j+1列及第2行第4j+2列元素为1,其余元素为0。现以3节点转子系统为例,当密封位于节点2处时,转换矩阵T₂为

则有

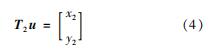
将式(4)代入式(1),则密封流体力可表达为

式中K^～、C^～、M^～分别为密封刚度系数矩阵、阻尼系数矩阵、惯性系数矩阵。

考虑到密封流体力矩阵与转子系统矩阵存在维度差异,利用转换矩阵对其进行扩维处理,获得扩维后的密封流体力Q^s,即

由式(5)、式(6)可得

Q^s=-T^T₂K^～T₂u-T^T₂C^～T₂u^·-T^T₂M^～T₂u^¨(7)

考虑密封力时,转子系统运动方程为

Mu^¨+Cu^·+Ku=Q+Q^s(8)

利用式(7)、式(8)将密封力直接耦合进转子系统刚度、阻尼以及惯性矩阵中,获得转子—密封耦合系统动力学模型为

(M+T^T₂M^～T₂)u^¨+(C+T^T₂C^～T₂)u^·+(K+T^T₂K^～T₂)u=Q(9)

将此推导扩展到一般情况,即当节点j处存在密封时,转子—密封耦合系统动力学模型为

(M+T^T_jM^～T_j)u^¨+(C+T^T_jC^～T_j)u^·+(K+T^T_jK^～T_j)u=Q(10)

为完成转子—密封系统的耦合求解,密封动力特性系数和转子耦合系统运动方程应分别进行求解,在求解运动方程的每一时间步内将所求解的密封动力特性系数引入转子运动方程中。图1给出了相应的求解流程,具体步骤如下:

1)确定初始参数,如转速、密封压力等;

2)基于有限单元法建立转子系统运动方程,即式(2);

3)计算当前转速及压差下的密封动力特性系数;

4)将计算获得的动特性系数引入式(2)形成转子耦合系统运动方程,即式(10);

5)求解式(10)获得当前工况下转子的响应及固有频率,并保存数据;

6)增加转子转速,重复前述步骤3)～步骤5),直至转速达到最大给定值,结束。

当完成所有时间步的求解之后,即可获得转子系统的坎贝尔图及相应的响应曲线。

图1 耦合求解流程图
Fig.1 Flow chart of the coupled solving method

涡轮泵实际运行过程中,密封两端压差会随转子运行转速变化而改变。因此,其引入的刚度阻尼系数也会随之发生变化,进而对转子系统动力学特性产生影响。

涡轮泵工作时,密封两端压差与离心泵扬程关系近似成正比^[23]。因此,基于离心泵相似定律,可认为不同转速下密封两端压差关系为

(Δp)/(Δp_d)=(n/(n_d))²(11)

式中:Δp和n分别为任意工况下密封两端压差及转速; Δp_d和n_d分别为额定工况时密封两端压差和转速。

本文研究的密封几何尺寸及运行参数如表2所示。

表2 密封几何尺寸及运行参数
Tab.2 Seal geometry and operating parameters

图4、图5分别给出了涡轮泵运行时密封刚度系数以及阻尼系数随工作转速的变化关系。可以看出,涡轮泵升速过程中,由于转速以及压差的共同作用,密封主刚度以及交叉刚度系数显著增大,并且随转速增大呈现近似二次曲线增大的趋势; 而主阻尼以及交叉阻尼系数随转速增大呈现线性增长的趋势。由此可知,对于高压高速涡轮泵,密封耦合效应应当受到重视。

图4 不同转速下的密封刚度系数
Fig.4 Seal stiffness coefficientat different working speeds

图5 不同转速下的密封阻尼系数
Fig.5 Seal damping coefficient at different working speeds

在进行转子系统动力学求解时,泵端轴承支承刚度取K₁=2.84×10⁸ N/m。考虑到涡轮端轴承座为柔性结构,选取涡轮端总支承刚度K₂范围1.35×10⁸～3.15×10⁸ N/m进行分析。

图6、图7分别给出了考虑密封耦合前后转子系统一阶、二阶临界转速随涡轮端支承刚度K₂的变化曲线。可以看出,密封流体作用对转子临界转速影响非常显著。未考虑密封时,一阶转速随K₂增加先增大后趋于稳定,二阶转速则呈现出线性增长的趋势。考虑密封后,由于密封辅助支承的影响,转子各阶临界转速均明显上升。

图6 不同K2下转子一阶临界转速
Fig.6 First-order critical speed of rotor at different K2 values

图7 不同K2下转子二阶临界转速
Fig.7 Second-order critical speed of rotor at different K2 values

对于一阶转速,随着K₂增大,密封影响作用显著增强。当K₂=1.35×10⁸ N/m时,一阶转速增加1 788 r/min(增幅8.13); 而当K₂增大到3.15×10⁸ N/m时,一阶转速上升9 267 r/min(增幅37.42); 对于二阶转速,考虑密封后临界转速显著上升,增加幅度近一倍之多,但随着K₂的增加,其值基本保持不变。

为对上述密封影响作用进行解释,选取两种刚度方案(K₂分别为1.35×10⁸ N/m、3.15×10⁸ N/m)进行分析。图8、图9分别为两种方案下有无密封时的转子系统坎贝尔图。可以看出,未考虑密封时,由于转子系统陀螺效应,正、反进动曲线呈现出平稳的增加、减小趋势,临界转速即为正进动曲线与1倍转频线的交点。考虑密封后,正反进动一、二阶涡动频率均发生了变化。由于零转速时,密封两端压差为0,辅助支承作用消失,此时转子涡动频率与未考虑密封时相同; 随着转速的增加,密封效应逐渐增强,此时在转子陀螺效应以及密封效应的共同作用下,正、反进动曲线不再呈现出平稳的增加、减小趋势。

图8 K2=1.35×108 N/m时坎贝尔图
Fig.8 Campbell diagram with K2=1.35×108 N/m

图9 K2=3.15×108 N/m时坎贝尔图
Fig.9 Campbell diagram with K2=3.15×108 N/m

由图8可以看出,K₂ =1.35×10⁸ N/m时,密封耦合作用对一阶正反进动曲线均有一定的影响。随着转速的增加,一阶正进动频率有所增加,但增加幅度不大,由此导致一阶转速上升1 788 r/min,增幅约8.13。然而,密封对二阶正反进动曲线的影响非常显著,随着转速增加,二阶正进动频率迅速增大,从而导致二阶临界转速大幅上升,增加幅度达138.96。

由图9可以看出,K₂=3.15×10⁸ N/m时,密封耦合作用对一、二阶进动曲线均有明显的影响。与图8相比,密封对一阶涡动频率的影响显著增强。随转速增加,一阶正进动频率迅速增大,从而导致一阶转速增加9 267 r/min,增幅达37.42。由于该型涡轮泵工作转速位于一阶转速附近,这一研究结果对于后续涡轮泵提速以及发动机性能提升至关重要。此外,与图8相似,密封影响下二阶涡动频率迅速上升,且上升的趋势相当,从而导致两种刚度方案下的二阶临界转速基本一致。

图 10、图 11分别给出了两种刚度方案下转子系统前两阶振型。由图 10可知,不考虑密封时,转子一阶振型为前后摆动,其中泵端摆幅较大,即密封处幅值较大。考虑密封后,振型发生变化,泵端摆幅减小,涡轮端摆幅增大,对应的一阶临界转速有所增加。此外可以看出二阶振型为弯曲振型,不考虑密封时,该振型的节点数目为0,而考虑密封后,节点数目变为2,对应的二阶临界转速显著增大。

图 10 K2=1.35×108 N/m时的振型图
Fig.10 Modal shape with K2=1.35×108 N/m

由图 11可知,当涡轮端支承刚度K₂增大到3.15×10⁸ N/m时,不考虑密封时,由于涡轮端刚度的增大,使得一阶振型为泵端摆动,而考虑密封后,泵端刚度的增大导致振型发生显著变化,成为涡轮端摆动,对应的一阶临界转速显著增大。而二阶振型变化情况与图 10相似,且考虑密封后的二阶振型与图 10一致,这也解释了考虑密封后二阶转速不随K₂变化的原因。

图 11 K2=3.15×108 N/m时的振型图
Fig.11 Modal shape with K2=3.15×108 N/m

为确定密封效应对转子系统不平衡响应的影响,表3、表4分别给出了两种刚度方案下涡轮泵稳定工作时轴端螺母、密封以及轴承处的不平衡响应。其中不平衡量按照ISO1940中G2.5平衡等级进行选取,并同相平均施加在诱导轮、离心轮和涡轮上。

表3 K2=1.35×108 N/m时不平衡响应
Tab.3 Unbalanced response with K2=1.35×108 N/m

表4 K2=3.15×108 N/m时不平衡响应
Tab.4 Unbalanced response with K2=3.15×108 N/m

可以看出,两种方案下,考虑密封后各部件的不平衡响应均大幅减小,降幅可达50以上。此外,当涡轮端支承刚度增大时,轴端螺母、密封处以及轴承1处的响应均有所增加,这是由于涡轮端支承刚度增大,泵端的相对刚度减小,而上述部件均位于泵端,因此不平衡响应值变大。

为了确定密封刚度以及密封阻尼对转子不平衡响应降低的贡献程度,对K₂=1.35×10⁸ N/m时不同密封刚度及不同密封阻尼下转子各关键部位不平衡响应进行了研究。

图 12给出了不考虑密封阻尼时转子各关键部位不平衡响应随密封刚度的变化曲线。可以看出,密封刚度对不平衡响应有一定的影响,随着刚度的增大,不平衡响应值降低,并呈现线性变化趋势,但变化程度并不显著。

图 12 不平衡响应随密封刚度的变化
Fig.12 Unbalanced response vs.seal stiffness

图 13给出了不考虑密封刚度时转子各关键部位不平衡响应随密封阻尼的变化曲线。可以看出,密封阻尼对不平衡响应影响非常显著,随密封阻尼的增大,不平衡响应迅速降低,而后逐渐趋近于0。

图 13 不平衡响应随密封阻尼的变化
Fig.13 Unbalanced response vs.seal damping

综上可知,密封效应对转子不平衡响应的影响是由密封引入的刚度阻尼效应共同所致,其中密封阻尼的影响起主导作用。

此外,由前面分析可以看出,上述各关键部件中,轴端螺母处的不平衡响应幅值最大。考虑到轴端振动关系到泵内端面密封的工作环境,因此选取该处的不平衡响应进行分析。

图 14、图 15分别给出了两种刚度方案下轴端螺母处的不平衡响应曲线。可以看出,随着转速增加,不平衡响应分别在各阶临界转速附近达到最大值。当不考虑密封时,由于转子系统阻尼较小,理论上在临界转速处不平衡响应将达到无穷大。当考虑密封后,由于密封阻尼的引入,临界转速处不平衡响应幅值大幅降低。但由于密封刚度对临界转速的影响,不平衡响应最大值的出现位置也出现了明显偏移。此外,刚度方案二下一阶转速处的不平衡响应较方案一明显增大,可能的原因为:一是由于方案二临界转速更高,由此引起的不平衡力更大; 二是该方案下轴端螺母处等效阻尼系数较小所导致。

图 14 K2=1.35×108 N/m时轴端螺母不平衡响应
Fig.14 Unbalanced response of the nut at shaft end with K2=1.35×108 N/m

图 15 K2=3.15×108 N/m时轴端螺母不平衡响应
Fig.15 Unbalanced response of the nut at shaft end with K2=3.15×108 N/m