基金项目:国家自然科学基金联合基金(U1967203)
作者简介:游尔胜(1992—),男,博士,助理研究员,研究领域为新型核动力技术及应用。
1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,四川 成都 610213; 2.清华大学 核能与新能源技术研究院,北京 100084
1. CNNC Key Laboratory of Nuclear Reactor Thermal Hydraulics Technology,Nuclear Power Institute of China(NPIC), Chengdu 610213, China; 2. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
effective thermal conductivity; model application; pellet bed reactors; nuclear thermal propulsion
当前,大推力运载火箭普遍采用液体燃料,存在着燃料携带量有限、推力不足、飞行时间短等问题,无法适应未来远距离载人飞行、大载荷星际货运等任务需求,需要探索开发以核反应堆技术为基础的新一代核动力火箭发动机[1-2]。早在20世纪50年代,美国、苏联等军事强国都开展了大量核热推进技术以及核动力火箭的研发工作[3-6],包括ROVER计划、NERVA项目、RD-0410发动机研发等。美国提出了近20种超热中子柱状石墨堆的设计方案,在内华达州建立了核热推进试验基地,并陆续完成了大量的地面试验,堆芯功率达到数千兆瓦,氢气出口温度高达2 000 K以上。苏联专门建造了3座核反应堆试验装置,并于1977年9月在“贝加尔”综合试验台上首次实现RD-0410发动机的物理临界,此后又陆续完成了功率运行和点火试验,验证了燃料材料、结构工艺等技术可行性。
核热推进反应堆设计过程中,堆芯流动传热计算分析是影响工质出口温度甚至反应堆系统安全运行的关键因素,需要开发特定的堆芯热工水力模型,以实现超高温度下燃料元件与气体工质之间的传热计算。另外,相比于压水堆核电站,核热推进反应堆为了在很高的功率水平下实现较小的体积和质量,堆芯通常设计为极高的功率密度,对堆芯换热过程的精细计算和数值模拟提出了很高要求,目前缺乏相应的传热计算模型。因此,本文针对颗粒床反应堆(pellet bed reactors,PBR)的设计方案,开展了气体工质与燃料元件混合介质的均匀化传热模型研究,为下一步堆芯设计和热工分析奠定基础。
从燃料元件和堆芯布置来看,核热推进的反应堆堆芯设计主要有六棱柱、颗粒床、异形燃料棒等。各自代表性的反应堆设计方案和主要性能参数如表1所示[3]。
颗粒床反应堆是美国布鲁克海文实验室(BNL)在高温气冷堆燃料颗粒的基础上提出的核热推进反应堆设计概念,包括旋转床和固定床两种。固定床可以采用双模式运行,即一方面通过H2开式循环产生推力,另一方面通过He闭式循环提供电能。直径500 μm左右的包覆型燃料颗粒填充在两个同轴布置的孔板中,形成环形的堆芯区域,并通过孔板上的小孔分布实现冷却剂的流量分配。20世纪80~90年代期间,美国国防部设想用核热推进器拦截弹道导弹,制定了Timberwind计划,后来改名为SNTP计划[7]。其中,颗粒床反应堆的研究最多,并延续了BNL的设计方案和研究成果。20世纪90年代末,Powell等[8]在颗粒床反应堆的基础上,发展出了MITEE小型核热推进发动机。与颗粒床反应堆相比,MITEE的热功率和推力分别只有75 MW和14 kN,但同时也减小了发动机的体积和质量,从而降低了研发难度。此外,美国新墨西哥大学[9-11]在颗粒床反应堆方面进行了长期探索研究,提出了用于核电推进、核热推进和双模式应用等多种形式的设计方案。
颗粒床反应堆的典型设计方案如图1所示,堆芯区域由两个开有一定直径小孔的圆柱形金属板围成,中间随机堆积有一定数量的燃料颗粒。冷却剂沿冷套管与慢化剂之间的环形通道(氢气腔)向下流动,从冷套管上的小孔流入堆芯,与燃料颗粒换热后从热套管上的小孔流出堆芯。夹在冷热套管间的颗粒床厚度大约为几毫米至几十毫米,冷套管采用铝或不锈钢作为结构材料,热套管采用涂覆有碳化铌和碳化钽的石墨作为结构材料,冷热套管上均开有非均匀分布的小孔。在冷套管的外围依次为冷却剂入口环腔和慢化剂。
颗粒床反应堆的氢气流动过程如图2所示。冷却剂流动时,首先进入慢化剂内的流通孔道,带走慢化剂内部沉积的热量,然后在堆芯上腔室混合,再进入慢化剂与冷套管间的入口环腔,随后径向流动,穿过冷套管、燃料床、热套管,进入元件中心的热氢通道,所有燃料元件的高温氢气在推力室汇合,经喷管排出,产生推力。尽管颗粒床内孔径较小,但是由于其厚度较小,而且设计为径向流动缩短了行程,因此整体的流动压降较小。同时,球形燃料颗粒增大了气体换热面积,强化了对流换热能力,从而进一步提高了堆芯功率密度。
颗粒床反应堆中使用的燃料颗粒有两种设计方案,如图3所示。一种是在TRISO燃料颗粒的基础上直接将其放大,做成直径为4~6 mm的包覆型燃料球; 另一种与球床式高温气冷堆的燃料球结构类似,即将TRISO燃料颗粒均匀弥散在石墨基体中,做成直径为8~10 mm的弥散型燃料球[12-13]。在相同的富集度和直径时,包覆型结构可以很大程度上增加核燃料的体积份额,从而提高金属铀装量。当核反应堆功率小于几百千瓦时,弥散型燃料球由于核燃料装载量太少,即使将TRISO燃料颗粒的填充率提高到50%以上,也很难达到临界装量要求。因此,核热推进反应堆为了追求极致的堆芯功率密度,一般选用包覆型燃料球,即大尺寸燃料颗粒进行堆芯设计。
颗粒床反应堆中使用的燃料颗粒是由多种材料组成的包覆型结构,其热物性与各种材料的热物性和体积份额有关。另外,有效导热系数是一个反映球床堆芯综合传热效果的参数,包含了气体与固体之间的导热、固体与固体之间的导热、固体表面的辐射换热、固体或气体与壁面之间的相互作用等多种机制。有效导热系数是颗粒床反应堆设计过程中一个至关重要的物理量,影响着燃料最高温度和堆芯内温度分布。
颗粒床反应堆的燃料颗粒是一个多层包覆结构,其密度和比热容可以分别由体积和质量加权平均得到,即
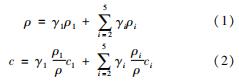
然而,燃料颗粒的导热过程不仅与各包覆层的导热能力有关,还与燃料颗粒尺寸、内热源大小等因素有关,不能简单进行体积或质量加权平均。本文假设燃料颗粒外表面和中心的温差一定情况下,将实际的多层结构简化成相同外径的均匀结构(见图4),得到燃料颗粒的均匀导热系数如式(3)所示。其中,燃料核芯和各包覆层的导热系数为常数。同时,假设均匀化的燃料颗粒与实际的燃料颗粒具有相同的裂变功率,即需要将燃料核芯的功率密度折算到整个均匀化的燃料颗粒上。
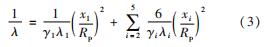
式中:x1为燃料核芯的半径; xi为其他包覆层的厚度; Rp为燃料颗粒的半径; γ1为燃料核芯的体积份额; γi为其他包覆层的体积份额。
对比二氧化铀(UO2)、氮化铀(UN)、碳化铀(UC)这3种常用的核燃料,可得直径5 mm的燃料颗粒均匀导热系数如图5所示。其中,燃料核芯外径和各层厚度分别为4.00 mm、0.25 mm、0.05 mm、0.15 mm和0.05 mm,如表2所示。燃料核芯的体积份额最大,为51.20%; 其次是疏松热解碳层,体积份额为21.70%。
从图5中可以看出,UN和UC燃料颗粒的导热系数随温度升高而增大,UO2燃料颗粒的导热系数随温度升高先减小后增大。总体来看,UN燃料颗粒的导热系数最大,在5.0~6.5 W/(m·K)之间; UC燃料颗粒的导热系数略小,在5~6 W/(m·K)之间; UO2燃料颗粒的导热系数最小,在1.0~2.5 W/(m·K)之间。当运行温度在1 700 ℃左右时,UO2燃料颗粒的导热系数最小,约为1.4 W/(m·K)。
氢气是目前已知密度最小的气体,三相点压力和温度分别为7.038 2 kPa和13.84 K,临界压力为1.296 4 MPa,临界温度为33.145 K,临界密度为31.263 kg/m3。由于氢气的分子量很小,一般作为火箭发动机的推进剂以尽可能提高比冲。根据Tsiolkovsky方程,如式(4)所示,提高发动机比冲可以降低初始与末级质量比,从而降低火箭发射时的初始质量或提高有效载荷的发射质量,使火箭发射任务降本增效。从已有数据来看[14-15],核热推进火箭发动机的比冲可以高达900 s,而目前最先进的液体火箭发动机的比冲约为450 s。
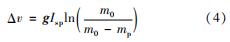
式中:g为重力加速度; Isp为发动机比冲; m0为火箭初始质量; mp为推进剂质量。
氢气的导热系数等物性参数在核热推进系统设计和反应堆热工分析中具有重要意义。从整个核热推进的热力学过程来看,氢气的状态参数变化很剧烈,可能从临界点迅速升高到约3 000 K,压力从常压升高到20 MPa左右。考虑到实际气体的分子间相互作用,氢气导热系数的半经验计算模型为[16]
λ(ρ,T)=λ0(T)+Δλ(ρ,T)+Δλc(ρ,T)(5)
式(5)中右边3项分别为理想气体直接贡献项、实际气体考虑分子间相互作用的附加贡献项,以及临界点附近由于密度脉动导致的临界增强项。其中,第一项通常表示为
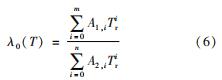
将该模型的计算结果与NIST数据进行对比,如表3和图6所示。可以看出,相同温度下二者的计算结果吻合得很好,大部分相对偏差在5%以内。氢气的导热系数随着温度升高而增加,从0.4 W/(m·K)增加到1.5 W/(m·K)左右。
有效导热系数与颗粒床堆积方式、气体和固体导热系数、燃料颗粒直径、孔隙率等多种因素有关,很难直接通过理论推导获得。一般情况下,需要将理论与实验相结合,在一些假设条件的情况下得到半经验关系式。1970年,德国学者Zehner和Schlünder在研究高温球床堆的有效导热系数时,使用圆柱体单元传热分析模型推导得到ZS关系式。该模型认为圆柱体可以分为内、外两个部分,内圆柱由固体和气体组成,外圆环全部为气体区域。同时,模型假设两个半球是点接触,内圆柱和外圆柱之间的传热为并联过程,内圆柱中固体和气体的传热为串联过程。模型中,Zehner和Schlünder对前人关于堆积结构的传质实验和颗粒间导热问题的研究进行了分析,得到颗粒床与气体扩散率之比与孔隙率的经验关系式如(7)所示。为了描述内圆柱中固体与气体交界面上的特征曲线,模型引入了形状因子,并通过特定孔隙率下球床均匀区域的传质实验获得。
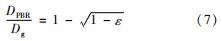
式中:DPBR为颗粒床平均扩散系数; Dg为气体扩散系数; ε为颗粒床孔隙率。
1978年,Bauer和Schlünder对ZS模型进行了补充,认为在外加载荷和球床自身重力的作用下,球体会产生变形。因此,相邻球体之间的接触不再是点接触,而应该是面接触。Bauer和Schlünder在ZS模型的基础上,还考虑了面接触、气体Knudsen扩散、辐射换热3种作用,整理出ZBS模型[17],即
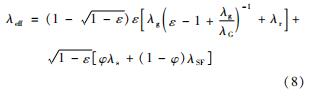
式中:λSF为内圆柱导热与辐射共同作用的等效导热系数,表示“固体导热→气体导热和辐射→固体导热”的传热过程; λg为气体导热系数; λG为气体等效导热系数,即考虑了气体分子在Knudsen扩散区域的Smoluchowski效应(气体分子热运动的能量涨落); λr为辐射等效导热系数; φ为燃料颗粒相互接触时的面积份额,即表面接触率。
表面接触率φ是一个衡量面接触大小的物理量,以往一般取某个经验系数进行粗略计算。根据表面接触率的物理意义,本文将其定义为总接触面积与球体表面积的比值,如式(9)所示。

式中:N为颗粒床的平均接触点数目; Rc为接触面的等效半径。从式(9)中可以看出,表面接触率与颗粒床堆积方式、颗粒直径等因素有关,从而能更加准确地反映出接触面的导热份额。
如图7所示,对于3种典型的规则堆积结构,即立方体堆积(SC)、体心堆积(BCC)和面心堆积(FCC),对应的颗粒床几何参数如表4所示,平均接触点数目分别为6个、8个和12个。对于其他孔隙率的随机堆积,可以通过孔隙率插值得到对应的平均接触点数目[18],即
N=1.008×10-2ε-4.785+5.648(10)
虽然当前民用核电站和核动力装置都选用二氧化铀做燃料,但氮化铀或碳化铀的导热系数大约比二氧化铀高出1个数量级,从而大幅降低燃料元件的中心温度,提高堆芯热工安全裕量。从图5中可以看出,当颗粒床堆芯温度为1 500 ℃时,3种燃料颗粒的均匀导热系数分别为1.43 W/(m·K)、5.97 W/(m·K)和5.58 W/(m·K)。选用氮化铀或碳化铀,燃料颗粒的导热系数是二氧化铀的4倍左右。因此,本文对二氧化铀、氮化铀、碳化铀3种核燃料的颗粒床有效导热系数进行了对比分析,如图8所示。
图8 核燃料对颗粒床有效导热系数的影响
Fig.8 The influence of nuclear fuel on the effective thermal conductivity of pellet beds
从图8中可以看出,3种燃料的颗粒床有效导热系数都随着温度升高而增大。特别是当燃料颗粒的表面发射率εr较大时,自身导热系数的差异对有效导热系数的贡献将越来越小,从而导致3种燃料的计算结果基本一致。对于低发射率和低运行温度,燃料导热系数对颗粒床有效导热系数的影响比较明显,氮化铀和碳化铀的导热系数更大,因此颗粒床有效导热系数也越大。当运行温度为1 500 ℃、 颗粒床孔隙率为0.32、表面发射率为0.10时,3种燃料的颗粒床有效导热系数分别为19.9 W/(m·K)、23.3 W/(m·K)和23.0 W/(m·K)。
燃料颗粒直径也是核热推进反应堆在堆芯设计时的一种重要参数。本文在假设外层包覆厚度不变的情况下,通过改变燃料核芯的直径,以改变燃料颗粒直径和颗粒床有效导热系数,如图9所示。燃料颗粒直径的变化范围从2 mm增加到6 mm,核燃料统一为氮化铀。
图9 燃料颗粒直径对颗粒床有效导热系数的影响
Fig.9 The influence of fuel pellet diameter on the effective thermal conductivity of pellet beds
从图9中可以看出,不同燃料颗粒直径的颗粒床有效导热系数同样随着温度升高而增大。在相同温度下,增大燃料直径有利于提高颗粒床有效导热系数。当运行温度为1 500 ℃、颗粒床孔隙率为0.32、表面发射率为0.10时,颗粒床有效导热系数从9.25 W/(m·K)增加到27.70 W/(m·K),后者约为前者的3倍左右。
核热推进反应堆堆芯由燃料颗粒随机堆积而成,其密实程度一般用孔隙率来表示。如表4所示,理论上立方体堆积(SC结构)的孔隙率最大,约为0.48; 面心堆积的孔隙率最小,为0.26; 其他随机堆积的颗粒床孔隙率在二者之间。因此,本文选取的孔隙率在0.26~0.48之间变化,对颗粒床有效导热系数进行了计算分析,如图 10所示。
图 10 孔隙率对颗粒床有效导热系数的影响
Fig.10 The influence of porosity on the effective thermal conductivity of pellet beds
从图 10中可以看出,不同孔隙率的颗粒床有效导热系数也是随着温度升高而增大。在相同温度下,颗粒床孔隙率越大,即燃料颗粒在堆芯中堆积得越松散,则气相体积份额越多、固相体积份额越少,导致燃料颗粒表面的辐射换热量越大,颗粒床有效导热系数也随之增加。当运行温度为1 500 ℃、燃料颗粒直径为5 mm、表面发射率为0.1时,有效导热系数从16.3 W/(m·K)增加到48.4 W/(m·K)。温度越高,有效导热系数随孔隙率增加的幅度越大,趋势越明显。
本文在颗粒床有效导热系数模型以及多层包覆燃料颗粒均匀化处理和氢气导热系数计算公式的基础上,对核热推进反应堆设计过程中可能用到的燃料种类、燃料直径、堆芯孔隙率等进行了对比分析,主要结论如下。
1)颗粒床有效导热系数随堆芯温度的升高而增大,主要是燃料颗粒表面的辐射换热作用占主导,从而使得燃料颗粒自身导热系数的贡献很小,即1 500 ℃以上高温运行时,颗粒床有效导热系数对核燃料的变化并不敏感,甚至几乎可以忽略不计。
2)燃料直径和堆芯孔隙率对颗粒床有效导热系数影响较为明显,相同温度下增加燃料直径或增加堆芯孔隙率都能使颗粒床有效导热系数变大,在1 500 ℃的运行温度下,有效导热系数增加为前者的3倍左右。
3)当堆芯运行温度逐渐升高时,不同核燃料、燃料直径以及堆芯孔隙率下,颗粒床有效导热系数都会逐渐增加且差异越来越大,可能从20~30 W/(m·K)增加到200 W/(m·K)左右。