基金项目:国家自然科学基金联合基金(U1967203); 四川省自然科学基金(2024NSFC1361)
作者简介:肖 辉(1993—),男,博士,助理研究员,研究领域为自然循环强化及多场协同调控。
1.中国核动力研究设计院,四川 成都 610213; 2.西安航天动力研究所 航天液体动力全国重点实验室,陕西 西安 710100
1.Nuclear Power Institute of China, Chengdu 610213, China; 2.National Key Laboratory ofAerospace Liquid Propulsion, Xi'an Aerospace Propulsion Institute, Xi'an 710100, China
convective heat transfer; flowing across tube bundles; liquid metal; weightlessness; gravity
在空间推进领域,低质量核能系统可提供高可靠性、可持续性和大功率动力源,因此成为太阳系边界探测、载人深空探测等空间更远区域探索任务的较好动力源方案[1-2]。此外,低质量核能系统还可实现核热推进与核电推进,具有实现高比冲、长寿命、多模式微小推力和宽功率范围等多种推进方案的潜力[3]。
液态金属具有优良的导热性能[4],将特殊液态重金属作为冷却工质的先进核能系统具有安全性能高、小型可移动、功率范围宽(千瓦-百兆瓦)的显著特点,加上一次装料可运行30年的长效优势,使其成为空间环境动力源的较优选择[5-6]。液态金属横掠管束对流传热能力强,相关换热器结构紧凑,便于火箭运载,是较好的主换热器形式[7-8]。空间环境异于地面环境,其显著特点是失重,对比研究失重和重力条件液态金属横掠管束流动传热特性可提升空间反应堆换热器设计能力。
液态金属的普朗特数Pr约为水、空气等常见工质的1%,量级为0.01,故对对流传热过程导热贡献较大,常规普朗特数流体对流传热公式不适用于液态金属[9-10]。文献[11-12]研究了钠、铅铋合金在绕丝棒束内的流动传热特性,表明了绕丝引起的二次流对流动传热影响较大。Richard等[13]研究了液态汞绕流管束的对流换热性能,得到了努塞尔数Nu为贝克莱数Pe的函数。Dwyer[14]根据实验结果拟合得到了液态金属对流换热关系式,公式可适用于Pe=50~7 000范围。近年来,赵后剑等[15-16]数值研究了液态铅铋绕流顺排管束流动传热性能,表明截距对传热性能影响较小。Yang等[17-18]数值研究了液态铅铋横掠螺旋管束流动传热性能,得到了最优结构参数Pr/D=0.167和Pa/D=0.137。沈聪等[19]数值模拟研究了铅铋螺旋管壳侧流动传热性能,表明阻力和换热均随着流速和螺旋升角增大而增强。总体而言,可查阅的液态金属横掠管束对流传热相关研究较缺乏[20]。此外,重力和失重条件下的液态金属横掠管束特性对比尚不清楚,现有地面实验也无法获得绝对失重条件下的流动传热特性。近年来,数值模拟技术为理论分析和工程实践提供了较好结果[21-22],成为了研究流动传热问题的可靠方法。为此,本文将开展数值模拟研究失重和重力条件下液态重金属横掠管束流动传热特性。
考虑到研究重点为重力和失重条件对流动传热性能的影响,采用了较常见的管间距和壁面结构。物理模型为实际换热器的简化结构,如图 1所示。模型内部管径为D,相邻管轴心截距Pl,截距比Pl/D为1.5。模型分为进口区域、测试区域和出口区域3个部分,长度分别为6D、21D和9D,高度Pt为1.5D,垂直纸面的横向宽度w为10D。模型竖直放置,高温液态金属从上往下横掠管束,管内为冷却工质,管壁厚2 mm,管外径14 mm,此时重力方向竖直向下。
为开展数值研究,采用如下假设:数学模型为三维模型且处于稳态条件; 流体质量连续且不受其他体积力; 忽略黏性耗散产热和辐射传热的影响; 采用k-ε Reliazable雷诺时均模型处理湍流脉动。相关控制方程如下。
连续性方程为
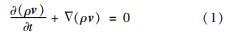
式中:ρ为密度; v为速度; t为时间。
动量方程为
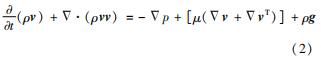
式中:p为压力; μ为动力黏度; g为重力加速度。
能量方程为
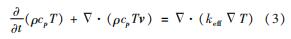
式中:keff为有效热导系数; cp为比热容; T为温度。
湍动能k和湍流耗散率ε满足
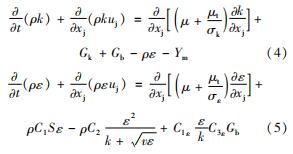
其中
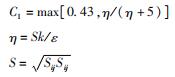
式中:C2 和C1ε均为给定的经验常数; 湍动能增量Gk由速度梯度引起; 湍动能增量Gb由浮力引起; Ym为脉动膨胀引起的湍流耗散率增量; σk为k的湍流普朗特数; σε为ε的湍流普朗特数。
液态金属普朗特数较低,对流传热过程热扩散贡献较大,湍流传热过程给定Prt≈1不适用[23]。对于液态金属,其湍流普朗特数Prt选择Cheng等[24]提出的模型,即
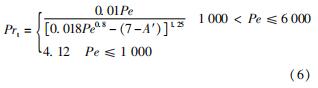
式中:Pe为佩克莱数; A'为常数。
液态金属入口为均匀速度和温度入口,壁面为无滑移边界,出口为压力出口。换热管壁面给定第三类边界,管内换热系数为20 kW/(m2·K),管内温度为553.15 K,管壁厚度为2 mm,其余壁面为绝热边界。考虑失重条件时,在动量方程中给定重力加速度为0。
主要无量纲参数有雷诺数Re、换热系数h、努塞尔数Nu和单排阻力系数f,相关定义如下
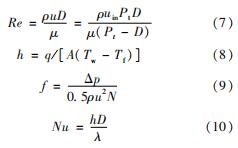
式中:q为平均热流密度; A为换热面积; N为管排数; Δp为流体摩擦压降; Tw为测试段管壁面积平均温度; Tf为流体测试段流体体积平均温度; f为测试段平均单排摩擦阻力系数。
对于液态金属物性,其物性参数为[9]
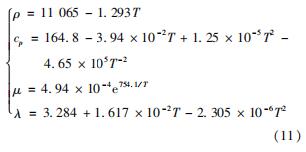
为选择合适的网格,对比分析了利用4套不同网格尺寸的网格系统计算得到的换热和阻力性能,如图3所示。采用单位体积网格数量描述不同网格系统的网格数量,4套网格的控制单元数量分别为:模型1为8.79×108个/m3,模型2为3.48×108个/m3,模型3为2.02×108个/m3,模型4为8.20×108个/m3。当网格系统从模型2变为模型1时,网格数量增加一倍,但流动换热性能基本不变,变化量小于3%。可以认为,模型2对应的网格系统已足够细密,对于阻力系数和换热系数,网格系统已经独立。
在换热方面,缺乏壳侧液态金属外掠顺排管束的实验数据,因此,本文选择液态金属钠的换热经验公式,通过对比相应横掠错排管束的Kalish-Dwyer公式[14]和数值模拟结果开展结果验证。在阻力方面,采用传热学推荐的错排管束经验公式[25]。相关公式表示为
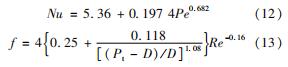
对比结果如图 4所示,经验公式结果和模拟结果之间偏差较小,两者吻合较好。换热性能最大偏差为16%,阻力系数最大偏差为19%。这表明当前湍流模型、湍流普朗特数模型以及数值模拟方法可靠且足够准确。
选取了Re=20 000的数值模拟结果,关注入口后管束区域的第3排和第4排传热管附近区域,对比了重力和失重条件相同截面位置温度场和速度场的分布,结果如图 5所示。温度分布结果表明,受到传热管内冷却流体的冷却作用,传热管附近温度明显降低,管壁附近流体最高温度和最低温度差可达80 K,最低温度出现在传热管背风面。重力和失重条件下温度分布差别较小,这是因为液态金属导热性能较强,导热在对流换热过程中贡献较多,而且绕流传热管混流强烈,尽管浮力会引起一些流场改变,但对流换热性能不会有较大改变。
图5 重力和失重条件下温度场和速度场对比
Fig.5 Comparisons of temperature field and velocity field between gravity and zero-gravity conditions
速度分布结果表明,流体绕流传热管时,传热管背风面会产生回流涡,回流涡搅浑了流体,可强化对流换热。传热管侧面流道变窄,该区域流速较大。对比失重和重力条件速度分布可知,重力条件下最大流速较小,这是由于传热温差引起的浮力对原本流场产生了影响,促使最大流速变化,进而导致阻力特性变化。
随着Re的增大,换热性能和阻力系数的变化规律如图 6所示。随着雷诺数的增加,Nu逐渐增加,失重和重力条件下的变化规律一致。在失重条件时,Nu稍大且Re较小时,偏大量越大,当前研究范围内失重条件比重力条件换热性能偏大量最大约10%。重力条件下换热性能偏小的原因是浮力作用对主流流动产生了抵抗,降低了其对流换热能力,但液态金属导热系数较大,对流换热能力降低不明显。
失重和重力条件下阻力系数变化规律基本一致。在失重条件下,随着Re增加,阻力系数逐渐减小; 在重力条件下,随着Re增加,阻力系数也逐渐减小,但减小幅度略大。当Re>10 000时,重力条件下阻力系数总是小于失重条件下的阻力系数,且随着Re增大,两者差距变小。这表明,对于液态金属竖直向下流动降温过程,密度增大引起流速降低,将降低绕流管束的流动阻力。然而,Re较低时(约小于10 000),浮力引起的二次流对主流流动的影响较大,会增大流动耗散,从而增大摩擦阻力。在本研究范围内,重力条件下和失重条件下的阻力系数最大偏差约为10%。
图6 换热性能和阻力系数随Re增加的变化规律
Fig.6 Variations of heat transfer and friction factor with the increase of Reynolds number
针对当前研究范围,给定第三类热边界条件,拟合了流动换热过程的阻力和换热关系式,其中失重条件下关系式为
Nu=-0.292 3+0.808 4Pe0.550 7(14)
f=0.166 3+5.724Re-0.361 9(15)
Nu和模拟结果的最大偏差为5.6%, f和模拟结果的最大偏差为0.8%。
重力条件下,对于给定的第三类热边界条件,流动换热关系式为
Nu=-0.653 5+0.695 8Pe0.573 3(16)
f=0.249 4+397.5Re-0.876 7(17)
Nu和数值模拟结果的最大偏差为10.9%, f和模拟结果的最大偏差为1.9%。
本文针对重力和失重条件下液态金属绕流传热问题开展了数值模拟研究,获得了流动传热过程的温度和速度分布,得到了流动传热特性随雷诺数的变化规律,拟合得到了流动传热关系式,在本研究范围内,得到如下结论。
1)基于雷诺时均的k-ε Realizable湍流模型结合Cheng等[24]提出的湍流普朗特数模型可用于获得可靠的液态金属绕流传热数值模拟结果,Nu、f与实验经验关系式偏差分别小于16%和19%。
2)绕流传热管附近温度分布不均,当前热边界下最大温差可达到80 K,绕流传热管背风面会产生回流涡,从而强化对流传热。
3)流动换热过程温度差会引起密度差,产生的主流流速改变和二次流引起流动传热性能发生变化,浮力对阻力和换热性能影响均小于10%。
4)拟合得到了重力和失重条件下流动换热阻力关系式,与数值模拟的偏差不超过10.9%。