1. 哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001; 2. 中国核动力研究设计院,四川 成都 610213
1. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China; 2. China Nuclear Power Research and Design Institute, Chengdu 610213, China
multi-stage compression; Brayton cycle; binary gas mixture; sensitivity analysis; Sobol-Sequence
1956年中国航天事业开始起步,秉持自主创新、重点跨越、支撑发展、引领未来的发展理念,历经多年蓬勃发展,成功开展了载人航天工程、空间站工程、探月工程等一系列的空间探测计划,并取得傲人的成就[1]。对于深空探测这类长距离的飞行任务,可靠的动力系统至关重要,先进的核电推进系统与完全非核方法相比,可以大大减少旅行时间[2]。相比于太阳能和化学能,核能所展现出的稳定高效、高能量密度、使用寿命长等特点,使其成为深空探测的首选动力来源[3]。
空间核动力成为各航天大国研究的热点问题。20世纪60年代开始,美国开展了采用氦氙混合工质的闭式布雷顿循环的系统样机试验计划,NASA研制出功率分别为10 kW和2 kW的BRU[4]和Mini BRU[5]两种热电转换装置。2003年,NASA喷气推进实验室开展“普罗米修斯计划”,设计JIMO轨道飞行器实现对木卫二、木卫三、木卫四的探测任务,该计划是NASA首次实施针对深空探测的核电推进项目[6]。2009年,俄罗斯科尔德什研究中心和尼凯叶特研究院联合设计兆瓦级核电推进系统(超高温气冷堆+闭式布雷顿循环+热管辐射散热),预计实现1 MW的电功率[7]。20世纪70年代,我国开始着手进行空间核动力方面的研究工作,由于当时太阳能技术的快速发展,空间核电技术进展相对缓慢,航天科技集团、中国原子能科学研究院和北京航空航天大学相联合,开始重点开展我国空间核动力系统[8]。
热电转换方式为空间核电推进的关键技术之一,其中静态转换利用材料本身的物理特性,转换效率一般在4%～10%之间[9]。而基于斯特林循环、朗肯循环和布雷顿循环的动态转换则利用旋转机械将热功转换为电能,并且效率可以达到10%～30%[9]。闭式布雷顿循环发电效率高,其热电转换效率可达到30%以上、系统简单可以进行小型化设计、安全可靠、寿命长,可以提高航行中的可靠性等。当系统输出功率达到兆瓦级以上时,布雷顿循环展现出的性能成功兼顾了热电转换效率和系统质量等方面性能需求[10]。
国内外学者从不同的角度围绕着闭式布雷顿循环系统的热力学参数和系统的性能优化进行研究。马同玲等[11]对闭式布雷顿循环的发电系统的热力过程进行了分析讨论,该循环基于简单的回热布雷顿循环系统进行,通过数学模型搭建得出其发电系统发电效率和比功率与透平机入口总压、透平机效率、压缩机入口总温度、压缩机压比等系数有关; 并且,系统的发电功率随压气机入口温度增加而降低,随压气机压比的增大而增大。田志涛等[12]对氦氙混合气体离心机进行分析,成功设计出单级压比为2.3、流量为1.6 kg/s的氦氙混合离心压气机。李智等[13]从热力学角度对空间反应堆布雷顿系统进行优化分析,该研究分别对比功和效率进行优化设计,比功优化模式在减小系统体积、质量方面具有优势; 但对于压气机级数,比功优化模式下对压气机的级数要求高于效率优化模式。张昊春等[14]对以CO2为工质的布雷顿循环空间核动力系统进行研究,增大压比虽然会造成回热效果变差,但会提高循环效率。
目前空间闭式布雷顿循环设计中,多数仍采用单级压气机的回热循环结构,压气机压比的提高将增加压气机的负荷,增加对压气机的性能要求。本文针对闭式布雷顿循环系统,通过增加压气机的级数建立多级压缩布雷顿循环模型改善系统的效率,降低对压气机的性能要求,使其更适应于比功优化模式。根据该热力学模型,研究系统参数对循环热效率等热力学性能的影响和变化规律,并进行优化以获得循环最优性能。
早期使用空气和氮气作为闭式布雷顿循环工质存在诸多问题,比如氧化和高温下的脆化问题,以及热交换效率低和流动阻力大等问题。而氦气,一种惰性气体,虽然能够解决这些问题,但其压缩难度带来了新挑战,研究发现,氦气和氙气的混合物在流动换热方面表现出更优秀的性能[15],惰性气体的物性如表1所示。氦气浓度的变化会影响工质的比热容、导热系数、动力黏度和普朗特数等热物理参数。氦气含量减少时将远离压气机的喘振线,减少氦气组分将减轻喘振对压缩机寿命和管道组件本身的影响[16]。此外,其他氦气的混合气体工质如超临界N2O-He等也在进行适应于布雷顿循环的研究[17-18]。
表1 常见惰性气体物性[19]
![表1 常见惰性气体物性[19]](2024年04期/pic149.jpg)
多数研究将混合气体视为理想气体进行处理计算,以分析气体混合工质在朗肯循环、布雷顿循环、斯特林循环等过程中的热力学性质。但对于大分子所组成的混合气体来说应将其视为非理想性气体,已获得准确的物理参数。非理性混合气体的准确模型将对热力学循环分析优化等研究起到重要的作用。
Chapman-Enskog方法能够较为准确地对稀疏的二元混合气体进行热物性预测,但由于闭式布雷顿循环中,系统气体工质的温度变化从300 K至1 400 K,并且系统压力从0.1 MPa变化至20 MPa。在该状态下,Chapman-Enskog理论不再适用。Tournier和EI-Genk等采用第二维里系数和第三维里系数来表示氦氙混合气体的非理想气体状态方程以确定物质之间的势能[20]。
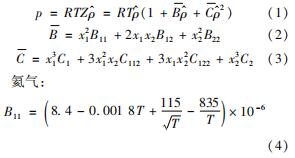
氙气:
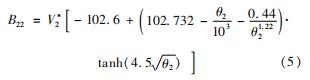
混合气体系数:
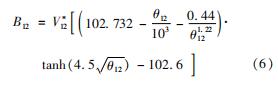
式中:θ1为气体的温度除以其临界温度; θ12为混合气体的温度除以其临界温度。
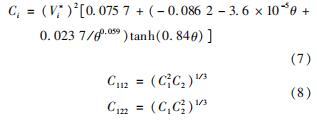
根据上述基于EI-Genk提出的混合惰性气体的非理想气体物性的计算方法,编写物性计算程序,并选用2 MPa的固定压强,400 K和1 200 K温度节点对不同摩尔质量的氦氙混合气体进行物性计算。计算结果如图1所示,其与标准数据[21]较高的吻合度,证明了计算程序的准确性。
图1 不同组分氦氙混合工质物性
Fig.1 Physical properties of different components of helium-xenon mixed working fluids
混合气体在1 200 K时,定压比热容和比热比与标准数据具有较好的吻合度,但在温度为400 K时出现一定偏差,根据计算可得误差最大值分别为0.7%和0.46%,计算过程中忽略该误差,认为计算模型与标准数据符合完好。
氦氙混合气体的定压比热容随着混合气体摩尔质量的增加而降低,当混合气体的摩尔质量小于40 g/mol时,混合工质的定压比热容随其摩尔质量变化较为明显,并且此时温度对混合工质定压比热容的影响较小。当混合气体的摩尔质量大于40 g/mol,温度为400 K时混合气体的定压比热容略高,此外在该范围内混合气体的定压比热容变化较为平缓。
根据计算结果可以看出,当摩尔质量小于20 g/mol时,随着混合气体摩尔质量的增加,普朗特数减小; 当混合气体的摩尔质量为20～60 g/mol时,普朗特数变化较为平缓,48.55 g/mol时普朗特数有最小值0.205 5; 当混合气体的摩尔质量大于60 g/mol时,普朗特数随混合气体摩尔质量的增加而增加。根据Tournier和EI-Genk提出的混合惰性气体的非理想气体物性的计算方法所得二元混合气体的定压比热容、比热比、普朗特数和导热系数与标准数据具有较好的吻合。
王志伟[19]进行了对纯氦、15 g/mol的氦氙混合气体和40 g/mol的氦氙混合气体的分析,结果显示40 g/mol的氦氙混合气体对叶轮机械的气动负荷影响最小,并且其传热系数与纯氦气体相同。并且根据EI-Genk等[22]研究结论,对于空间核动力系统应用,分子量小于等于40～45 g/mol的氦氙混合气体有利于装置的小型化。因此,选用氦氙混合气体的摩尔质量为40 g/mol。
针对后续多级压缩布雷顿循环热力学计算过程固定氦氙混合气体的摩尔质量为40 g/mol,温度变化范围为400～1 200 K,压力节点选取2.5、2.0、1.5、1.0、0.5 MPa进行计算,结果如图2所示。
图2 40 g/mol氦氙混合气体物性随温度变化
Fig.2 Physical properties of 40 g/mol helium-xenon mixed gas with different temperatures
40g/mol氦氙混合气体的定压比热容的随温度的增加而减少,当温度大于800 K时,其变化较为平缓。并且在该范围内,不同压力下混合气体的定压比热容相差较小,变化范围约为519～519.75 J/(kg·K)。比热比在不同压力节点中,温度变化在400～1 200 K时其变化并不明显,近似为1.67。
布雷顿循环的功率转换范围很广,是多个国家开发大功率空间核动力的重要研究方向之一。理想的布雷顿循环包括4个工作过程:膨胀机中的绝热膨胀、热交换器中的定压放热、压气机中的绝热压缩和加热器中的定压加热。提升循环效率的关键方式是降低压气机所产生的压缩功,可通过降低压气机入口温度、分级压缩、中间冷却和分流混流等方式,因此对于第二级压气机的入口添加间冷器来降低压缩功,工质通过间冷器后温度进行近似处理,其与冷源出口温度即第一级压气机入口温度相等。
采用分级压缩的方式,其总体压比与单级压气机相同,因此对于透平机并未产生较大影响,其主要影响为压气机的压缩功和压气机的性能要求的降低,循环采用离心式压气机进行分析计算。Gallo等[4]对空间反应堆布雷顿单元进行分析计算,根据计算结果绘制出40 g/mol氦氙混合气体为工质的压气机性能参数的变化,如图3所示。当混合工质流量为2.4 kg/s时,压比为1.28时压气机的额定转速为4.0×104 r/min,压比为1.66时压气机的额定转速增加到5.5×104 r/min,在相同的工质流量下,压比越大压气机的额定转速越大。
![图3 40 g/mol摩尔氦氙混合工质时压气机的性能参数[4]<br/>Fig.3 Performance parameters of a compressor at 40 g/mol helium-xenon mixed working fluid[4]](2024年04期/pic152.jpg)
图3 40 g/mol摩尔氦氙混合工质时压气机的性能参数[4]
Fig.3 Performance parameters of a compressor at 40 g/mol helium-xenon mixed working fluid[4]
压气机的入口和出口的速度三角形如图4所示,其中v1为进口的绝对速度; w1为进口的相对速度; u1为进口的周向速度; v2为出口的绝对速度; w2为出口的相对速度; u2为出口的周向速度。
压气机进口处速度参数分别为
图4 压气机速度三角形
Fig.4 Velocity triangles of compressor
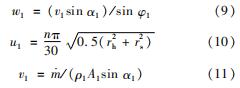
压气机出口处速度参数分别为
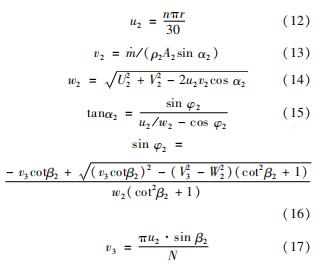
根据维里系数对理想气体状态方程的修正可得混合气体在节点处的密度为
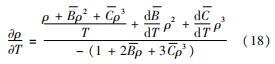
压气机进口和出口工质物性参数可近似根据式(19)计算,根据Bruno等设计的压气机参数可知,当混合工质流量为2.4 kg/s时,压比为1.28,额定转速为40 kr/min时效率为81.5%; 压比为1.66,额定转速为5.5×104 r/min时效率为83.4%。
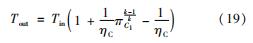
压气机负荷可根据欧拉方程解得,即
wc=v2cos α2u2-v1cos α1u1(20)
压气机具体设计参数如表2所示,根据上述数学模型和压气机设计参数对Bruno等所设计的压气机在压比为1.28和压比为1.66两个数据节点进行压气机负荷计算。
表2 40 g/mol氦氙混合气体的压气机设计参数[4]
Tab.2 Design parameters for a 40 g/mol helium-xenon gas mixture[4]
![表2 40 g/mol氦氙混合气体的压气机设计参数[4]<br/>Tab.2 Design parameters for a 40 g/mol helium-xenon gas mixture[4]](2024年04期/pic154.jpg)
计算结果表明,压比较低的压气机工质出口的绝对速度为153.15 m/s,压气机的负荷为17.362 kW; 压比较高的压气机工质出口的绝对速度为188.58 m/s,压气机的负荷为36.97 kW。因此,压比的降低可以有效降低压气机的负荷和压气机出口处工质的绝对速度。
图5为多级压缩布雷顿循环系统。1→2过程氦氙混合工质在涡轮处膨胀做功; 2→3过程涡轮出口具有较好品质参数的气体工质在回热器中对冷端气体进行回热过程; 3→4过程回热后通过冷源降温以降低压缩机进口温度; 气体工质进入压缩机,通过4→5过程的第一级压缩机、5→6过程的间冷器和6→7过程的第二级压气机; 7→8过程通过回热器冷端的气体后通过反应堆部分进行加热膨胀重复上述循环过程。
图5 多级压缩布雷顿循环模型
Fig.5 Multi-stage compression Brayton cycle model
相较于单级压缩回热式布雷顿循环,多级压缩仅在压气机部位增加级数,其余部件并未发生改变。单级和多级压缩布雷顿循环模型部分节点关键参数如表3所示。
表3 循环关键参数
Tab.3 Key parameters of cycle
涡轮出口参数为
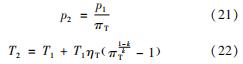
冷源散热器为
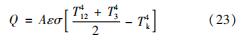
式中:A为面积; ε为发射率; σ为黑体辐射系数; Tk为宇宙背景温度。
热端回热过程为
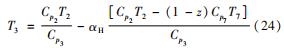
多级压缩过程为
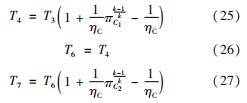
冷端回热过程为
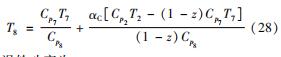
涡轮功率为
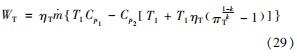
发电功率为
WE=ηEWT(30)
压气机耗功为
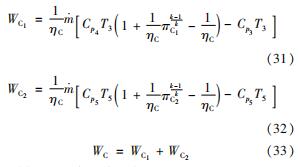
循环过程中吸热量为
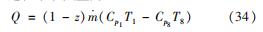
净效率为
ηth=(WT-WC)/Q(35)
布雷顿单元由压气机、膨胀机和发电机这3部分组成,其质量可通过式(36)进行计算,其中经验常数为1.8[18, 24]。
布雷顿单元质量模型[25]为
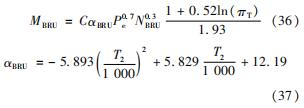
根据游尔胜等[25]关于布雷顿空间核能系统的质量估算模型的计算,布雷顿单元质量占总质量的26.4%。
根据氦氙物性模型和布雷顿循环模型,循环最高温为1 200 K,循环最低温度为400 K,压气机出口压强为2 MPa,分析间冷器引入对循环热力学性能的影响,如表4所示。第一级压气机和第二级压气机之间间冷器的引入,虽然对工质的热能未能有效利用,降低了冷端回热器出口的温度,进而提高了工质通过反应堆处的吸热量,但由于其有效降低压气机入口温度的同时,降低了系统的压气机所产生的压缩功,其对压缩功的影响程度高于系统的吸热量,进而提高了系统的热效率。根据计算结果可知,间冷器的引入对系统热效率的提升起到积极作用,因此多级压缩布雷顿循环模型在压气机之间可引入间冷器进一步提高系统性能。
表4 间冷器对循环性能参数影响
Tab.4 Effect of intercooler on cycle performance parameters
同样根据上述参数进行计算,对比多级压缩和单级压缩对循环性能的影响,计算结果如表5所示。增加压气机的级数有效地提高了系统的净效率,但由于压气机的增加导致循环的比质量提升,此外压气机的增加有效降低了对单一压气机的性能要求,在相同的性能要求下降低了对压气机的负荷,有效提高了压气机的可靠性和使用寿命,对于长时间的深空探测任务提供有利的保障。
表5 循环性能参数对比
Tab.5 Comparison of cycle performance parameters
不确定性参数广泛存在于实际工程问题中,因而需要正确且有效地评估不确定性参数对模型的影响程度。通常上述分析过程被称为敏感性分析,在敏感性分析中,大部分文献采用的分析方法是基于导数分析,其方法在节约计算时间上是有效的,仅仅只需要在运行模型几次即可推导出导数矩阵得出结果。马同玲等[11]依据导数分析的方法,对闭式布雷顿循环发电系统的热力过程及其参数影响进行敏感性分析。但该方法是有缺陷的,基于导数方法的参数影响研究仅仅在计算导数的这一点是有效的,不能涵盖其输入空间。该导数方法对于线性系统来说是具有一定的准确性,在一点上的偏离程度能够用一阶导数表示,但对于非线性系统来说却不再适用。
Sobol敏感性分析方法是由俄罗斯学者在1993年首次提出的全局敏感性分析的方法[26]。该方法采用基于方差分解的方式,将函数模型分解为单个参数以及参数之间的组合,从而计算单个参数和参数集的方差对目标值方差的影响,对于非线性和非单调函数模型能够快速地计算出各个输入参数对响应值的影响,其影响程度可由一阶影响因子和总效应指数获得。
Sobol-Sequence方法:对含有N个自变量数的目标函数,选用M个采样样本数。随机生成M行2N列的样本矩阵。将矩阵的N列设为矩阵A,后N列设为矩阵B。根据矩阵A和B进行构造矩阵ABi,利用矩阵B中的第i列替换矩阵A中的第i列。得到A、B、ABi矩阵,通过式(38)～式(39)进行计算一阶影响因子和总效应指数。
一阶影响因子为
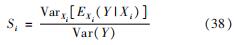
总效应指数为
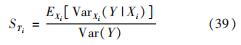
其中:
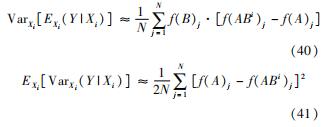
式(40)～式(41)对应函数f=(x1,x2,…,xn),有
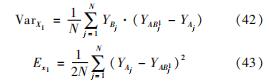
依据上述Sobol Sequence方法,编写程序对多级压缩布雷顿循环中的参数进行敏感性分析计算。各参数具体的变化范围如表6所示。
表6 循环关键参数在设计点附近变化范围
Tab.6 Variation range of the key parameters of the cycle near the design point
对于系统的热效率如图6所示,其一阶影响因子和总效应指数所呈现的结果近似相等。在该变化范围内,循环膨胀机和压气机的效率对系统热效率起到主要影响作用,在相同的波动范围内,压气机效率的影响程度略高于膨胀机效率的影响; 在相同的压比变化范围,第一级压气机压比对热效率的影响大于第二级压气机的影响。循环回热度对系统性能的影响较小,近似为零。
图6 热效率的一阶影响因子和总效应指数
Fig.6 First-order influencing factor and total effect index of thermal efficiency
对于系统的比质量如图7所示,总效应指数与一阶影响因子结果并不相同。在比质量的一阶影响因子中,占据主导地位的因素为膨胀机入口温度和第一级压气机压比,并且在相同的波动范围膨胀机效率对比质量的影响程度大于压气机效率的影响。当结合参数集之间的相互作用考虑对系统性能参数方差的影响,压气机效率和膨胀机效率占主导地位,在相同的压比变化范围内,第一级压气机压比影响程度大于第二级压气机压比的影响,循环回热度的影响近似为零。
图7 比质量的一阶影响因子和总效应指数
Fig.7 First-order impact factor and total effect index of specific quality
通过对循环热效率和系统比质量的计算可以获得不同参数对循环性能的影响程度,总效应指数相较于一阶影响因子考虑参数集的影响后,对于非线性的复杂模型更有效。其可对多级压缩布雷顿循环系统的优化起到重要的指导作用,考虑不同参数的实际变化范围,以总效应指数和一阶影响因子作为对比依据,可选出更具优化潜能的参数,提高优化效率。
通过总效应指数和一阶影响因子的计算可以了解不同参数对于系统性能的影响程度,对于复杂的非线性模型,总效应指数更好地考虑到参数集之间的相互影响,相较于一阶影响因子更精确地表明了不同参数对输出值方差的影响程度。全局的敏感性分析的计算可直接得出对目标值更具影响的参数但总效应指数只能反映其影响程度,并不能明确表示其变化趋势,因此为更直观地观察参数具体的影响趋势进行如下热力学分析。
固定其他参数,第一级压气机压比变化范围为1.1～2.6,选取4个循环最低温温度节点400 K、415 K、430 K和445 K,计算系统热效率和比质量随第一级压气机压比变化,结果如图8和图9所示。
图8 系统BUR单元质量和比质量随压气机1压比变化
Fig.8 The mass and specific mass of the BUR unit of the system varies with the pressure ratio of the first stage compressor
布雷顿单元质量随着压比的增加先增加到最大值后开始下降,在压比增加的最初阶段,布雷顿单元质量增加导致系统比质量的增加。当布雷顿单元质量开始下降时,由于压比的增加提高了压气机的耗功,导致系统净输出功的降低,且净输出功的降低程度远大于布雷顿单元质量下降的程度,因此该阶段系统的比质量依旧增加。因此系统的比质量随着第一级压气机压比的增加而增加。
图9 系统热效率随压气机1压比变化
Fig.9 The thermal efficiency of the system varies with the pressure ratio of the first stage compressor
随着一级压气机的压比增加,系统的净热效率逐渐增加。其增加趋势在压比较低时比较迅速,当压比π1=1.24时,不同循环最低温度的情况下均出现效率的最大值,后随着压比的增加而降低。压比的增大在增加压气机耗功的同时提高了膨胀比使膨胀机的输出功率和系统净输出功率增大,从而提高了循环热效率。当压比相对较小时,压力接近临界压力,压缩过程的功耗较小,热效率增长较快。此外,在相同的第一级压比的条件下,循环最低温度越低循环的净效率越高。
循环的最低温为400 K时,当压比π1=1.24时循环热效率最高为22.6%,压比超过1.24时,压缩过程中的功率消耗占涡轮机输出功率的比例增大,热效率降低。此外当压比较高时,压气机的出口压力较大,会对系统造成较为严重的问题,如密封问题,削弱材料的极限抗拉强度,使系统运行不稳定。
固定其他参数,第二级压气机压比变化范围为1.1～2.6,选取4个第一级压气机压比节点1.22、1.42、1.62和1.82,计算系统热效率和比质量随第二级压气机压比变化,结果如图 10和图 11所示。
图 10 系统BUR单元质量和比质量随压气机2压比变化
Fig.10 The mass and specific mass of the BUR unit of the system varies with the pressure ratio of the second stage compressor
图 11 系统热效率随压气机2压比变化
Fig.11 The thermal efficiency of the system varies with the pressure ratio of the second-stage compressor
与第一级压气机压比变化趋势相同,系统的热效率均随着压比的增加先增加后降低,但第一级压比的大小将对第二级压气机压比产生影响,第一级压比越小系统达到效率最大值时第二级压气机压比越大。随着第一级压气机压比的提升,系统达到效率最大值所对应的第二级压气机压比π1=分别为1.41、1.31、1.26和1.21。对于系统的布雷顿单元质量和比质量,变化趋势和第一级压气机压比π1相同,系统的布雷顿单元质量达到最大值时所对应的第二级压气机压比随着第一级压气机压比的提升而增加。
系统叶轮机械的功率对系统热效率的比质量的影响如图 12和图 13所示。系统的效率随膨胀机效率和压气机效率的增加而线性增加,系统比质量随膨胀机效率和压气机效率的增加而降低。当叶轮机械的效率大于85%时,叶轮机械效率的增加对系统比质量降低的效果并不明显。
图 12 系统比质量随膨胀机效率和压气机效率变化
Fig.12 The specific mass of the system varies with expander efficiency and compressor efficiency
图 13 系统热效率随膨胀机效率和压气机效率变化
Fig.13 The thermal efficiency of the system varies with the expander efficiency and the compressor efficiency
当系统的循环最高温在1 100～1 400 K内变化时,多级压缩布雷顿循环系统的净效率和比质量相对于循环最高温的变化如图 14所示,并选取不同的绝热系数节点。循环最高温的增加提高了膨胀机进口温度,导致循环的膨胀功增加,因此系统的净热效率随循环最低温的升高而升高。随着膨胀功的增加,系统布雷顿单元质量增加,且增加程度大于循环净功的增加,因此循环的比质量随着膨胀机入口温度的增加而降低。
图 14 系统热效率和比质量随绝热系数变化
Fig.14 The thermal efficiency of the system varies with the expander efficiency and the compressor efficiency
由于物性计算时,氦氙混合工质的比热比变化范围较小,计算过程选择0.40、0.41、0.42和0.43这4个绝热系数节点进行比较,其对系统净热效率的影响并不明显,当循环最高温大于1 350 K时,不同绝热系数的循环净效率近似相等,在循环最高温变化范围内绝热系数的变化对系统比质量的影响近似可以忽略。
根据上述分析可以发现在这种多级压缩布雷顿循环中,压气机的压比等参数对系统的特性影响重大。每个关键参数对系统的效率和比质量有不同的影响,且在实现最大效率和比质量时,对应的压比不能同时达到最大值。为了在给定范围内实现最佳效率和比质量,需要使用优化算法进行优化,已获得不同情况下的最优解。
在敏感性分析当中,虽然压气机效率和膨胀机效率对循环整体性能具有较高影响,但由于其和循环性能的关系近似正相关,压比对循环性能的影响虽然相较于叶轮机械较小,但是由于第一级和第二级压比的相互影响,因此选用其作为约束条件。
采用多目标粒子群算法,引入Pareto最优原则,将个体进行分层排序,基于它们之间的相互支配关系,这种方法的引入极大地提升了算法在多目标优化问题中的性能[27]。计算过程中对循环第一级和第二级压气机压比进行约束,压比的变化范围为1.2～2.6,目标函数为循环系统的热效率和比质量,并在计算过程中改变多目标粒子群算法中的变异参数,获得两组数据曲线如图 15所示。
图 15 系统热效率和比质量的Pareto前沿曲线
Fig.15 Pareto frontier curves of system thermal efficiency and specific mass
通过多目标粒子群算法的计算对上述参数进行分析,获得了针对于比质量和净效率Pareto最优解,如表7所示。对于不同的最优解所对应参数不同,当其他参数固定时,在该情况下效率获得最大值接近23%。在实际应用过程中可以针对不同的任务需要对不同参数进行选取,已获得最满足当前需要的最佳设计参数。
表7 双目标优化Pareto最优解集
Tab.7 Dual-objective optimization of Pareto optimal solution set
本文在原有回热式布雷顿循环的基础上,通过增加压气机级数构建了多级压缩布雷顿循环模型,并研究了不同关键参数下系统的效率和比质量,从热力学角度进行多目标优化,得到如下结论。
1)通过氦氙物性模型和多级压缩布雷顿循环数学模型的计算,在相同的参数条件下多级压缩布雷顿循环热效率为22.33%,优于单级压气机的布雷顿循环17.75%的热效率。增加压气机的级数有效地提高了系统的净效率,但由于压气机的增加导致循环的比质量提升,此外压气机的增加有效地降低了对单一压气机的性能要求,在相同的性能要求下降低了对压气机的负荷,有效地提高了压气机的可靠性和使用寿命,对于长时间的深空探测任务提供有利的保障。
2)根据Sobol敏感性分析方法,得到对多级压缩布雷顿循环更具优化潜能的参数,如叶轮机械效率、膨胀机和压气机入口温度、压气机压比等参数。循环的最低温为400 K时,当压比π1为1.24时循环热效率最高为22.6%,并且第一级压比越小系统达到效率最大值时第二级压气机压比越大。随着第一级压气机压比的提升,系统达到效率最大值所对应的第二级压气机压比分别为1.41、1.31、1.26和1.21。布雷顿单元质量随着压比的增加先增加到最大值后开始下降。当布雷顿单元质量开始下降时,由于压比的增加提高了压气机的耗功,导致系统净输出功的降低,且净输出功的降低程度远大于布雷顿单元质量下降的程度,因此该阶段系统的比质量依旧增加。绝热系数对系统的热效率和比质量的影响较小近似可以忽略。
3)通过多目标粒子群算法进行多目标优化,获得了针对比质量和净效率的Pareto最优解。仅限制压气机压比的情况下,效率最大值接近23%。在实际应用过程中可以针对不同的任务需要对不同参数进行选取,已获得最满足当前需要的最佳设计参数。
