驱动单元转子系统采用拉杆组合式结构。气体箔片轴承技术是转子系统的核心技术,也是系统的核心组成部分。径向气箔轴承由顶箔、波箔和轴承外圈组成。止推气箔轴承由平箔、波箔和轴承底板组成。
4.1 径向气箔轴承静动特性
径向气箔轴承的性能主要取决于顶箔和波箔的接触变形。本文基于有限单元法,对顶箔弹性变形采用不同单元类型进行表达,结合有限差分求解压力控制的雷诺方程和气膜厚度方程,再积分求解承载力和偏位角,通过轴承静特性的计算结果对比,选取最准确的模型获取轴承的动特性。对于等温条件下的理想气体Reynolds方程推导,进行如下假设:
1)忽略气体惯性力的作用。
2)间隙内的流动为层流。
3)忽略气膜法向的流动。
4)介质为牛顿流体,符合牛顿黏性定律。
经推导,得到无量纲Reynolds方程为
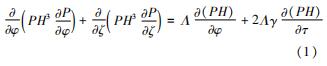
其中
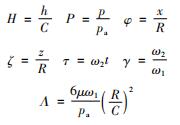
式中:x为周向坐标; z为轴向坐标; p为气膜压力; h为气膜厚度; μ为气体动力黏度; R为转子半径; ω1为转子角速度; t为运转时间; C为半径间隙; pa为轴承环境压力; ω2为转子涡动角速度; φ为偏位角; Λ为轴承数。
图6描述了结构为一端固定一端自由的整周式气箔轴承运动参数和结构参数,图中Ft和Fn为气膜分力。表3所示为布雷顿系统径向气箔轴承参数。
图6 气箔轴承运动和结构参数
Fig.6 Structure and motion parameters of gas foil bearing
表3 气箔轴承参数
Tab.3 Parameters of gas foil bearing
在气箔轴承计算模型中,对顶箔变形分别采用欧拉梁模型和厚板模型进行表达,使用有限差分法求解压力控制的Reynolds方程,通过MATLAB构建流固耦合模型进行计算。
图7所示为轴承的承载力一定时,不同顶箔模型计算得到的顶箔变形。从图中可知,厚板模型沿轴向变形较为明显,而欧拉梁模型则沿轴向无变形。这是由于具有节点五自由度的厚板单元考虑了剪切变形的影响,剪切力产生了剪切变形且附加的挠度不同。
图7 顶箔变形
Fig.7 Deformation of top foil
图8为偏心率相同(即e/C相同)时,两种模型下计算得到的轴承承载力和偏位角变化情况。随着转速升高,两种模型的偏位角变化基本一致,且表现出随转速升高逐渐降低的趋势,承载力则随转速升高而增大。但两种模型承载力的差异性逐渐变大,这是由于箔片沿轴向变形改变了气膜厚度和气膜压力的分布,引起承载力发生变化。厚板模型真实表现了气膜压力和厚度沿轴向的分布情况,因此,该模型得到的轴承动态刚度和阻尼系数更加准确。
图8 静态特性对比
Fig.8 Comparison of static characteristic
采用厚板模型,在静态特性计算基础上使用小扰动法得到气膜压力微分量与位移、速度的关系,应用有限差分法进行求解,得到轴承的动态特性系数。
升速过程等同于转子扰动频率逐渐增大,如图9所示,轴承刚度直接项Kxx和Kyy同时先减小再增大,在额定工况下轴承刚度直接项的各向异性最大。刚度交叉项Kyx的绝对值随扰动频率增大而减小并且趋于0,而交叉项Kxy逐渐增大,在额定工况与交叉项Kyx约反对称。阻尼直接项与交叉项随扰动频率增加逐渐趋于定值。
图9 升速过程转子扰动对动态系数的影响
Fig.9 Effect of rotor disturbance on dynamic coefficient during raising speed
4.2 临界转速与线性轴心轨迹计算
对转子系统进行动力学分析时将转子结构按刚度和质量等效,建立相应的计算模型。采用 Timoshenko 梁理论和有限单元法进行转子系统的临界转速计算。图 10所示为额定工况时转子系统的坎贝尔图,表4是由坎贝尔图得到的系统前三阶临界转速,可知工作转速距离三阶安全裕度约74.8%,安全裕度较大。
图 10 坎贝尔图
Fig.10 Campbell diagram
表4 系统前三阶临界转速
Tab.4 The first three critical speeds of the system
由于气箔轴承刚度和阻尼的变化,图 11描述了驱动单元升速过程转子系统临界转速变化情况。为使转子系统可靠运转,工作转速n需满足以下条件[20]:ncr2≤0.7n且ncr3≥1.4n。观察图 11可知,满足上述条件的最低工作转速为13 090 r/min,该转速为闭式布雷顿系统驱动单元最低起飞转速。系统工作时,由电机带动转子系统起飞,闭式系统达到最低起飞转速并稳定运行后,电机转为发电运行状态,系统缓慢升速至43 000 r/min,达到额定运转工况,由此,定义最低起飞转速为自持转速。
图 11 系统临界转速变化情况
Fig.11 Variation of system critical speed variation
图 12描述了转子系统的前三阶振型。一阶表现为俯仰刚体振型,转子系统两端异相回转(相位差180°),转子应变能为0.267%; 二阶表现为平动刚体振型,转子应变能为1.65%; 三阶振型为弯曲振型,转子应变能为96.3%。前两阶为刚体振型,振动应变能主要集中在轴承处,第三阶应变能主要集中在轴内。
图 12 转子系统的前三阶振型
Fig.12 The first three vibration modes of the rotor system
图 13描述了压气机端轴承和涡轮端轴承处转子的线性轴心轨迹。驱动单元达到自持转速后压气机端轴承处和涡轮端轴承处轴心轨迹表现均为椭圆,在达到额定转速后近似为圆,其原因为转子系统起飞后随转速升高,主刚度项逐渐增大,且表现出明显的各向异性,尽管额定工况时交叉刚度项接近于反对称,但主刚度项的各向异性更有利于转子稳定。
图 13 线性轴心轨迹
Fig.13 Steady-state rotor orbit