基金项目:国家自然科学基金(U23B6009,12272050)
作者简介:王 博(1996—),男,博士,研究领域为射流雾化的实验与数值模拟。
通信作者:陈晓东(1982—),男,博士,副教授,研究领域为多相流动力学、航空宇航推进。
1.北京理工大学 医学技术学院,北京 100081; 2.北京理工大学 宇航学院,北京 100081
1.School of Medical Technology, Beijing Institute of Technology, Beijing 100081, China; 2.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
impinging jet atomization; proper orthogonal decomposition; liquid film breakup; impact wave
DOI: 10.3969/j.issn.1672-9374.2024.06.006
撞击射流雾化是利用液体射流的碰撞将液体由射流转化为一个薄液膜,之后液膜本身具有的不稳定性会不断发展,最终使得液膜破碎分解成为离散的小液滴,实现了液体的雾化[1]。在撞击射流喷嘴中,最简单且最常见的结构是两个相同的液体射流以锐角碰撞,通常被称为互击式喷嘴。该结构因其结构简单、成本低、可维护性好以及良好的雾化性能和燃烧效率,被广泛应用于液体燃料火箭发动机当中。例如,在美国的阿波罗登月项目中,土星五号运载火箭第一级的F-1发动机在主燃烧室和气体发生器中都使用了撞击射流式喷嘴[2]。因而,对于液体火箭发动机,撞击射流雾化是一种非常有效的雾化和混合方法,阐释并解析撞击射流雾化的动态过程和作用机制将有助于优化撞击射流喷嘴的设计[1]。
液膜的破碎主要是由两个具有空气动力和水动力起源的大尺度波决定的[3]。空气动力波是由于气液界面的剪切,导致一个相对平坦的液膜在下游区域破碎,而水动力波(称为撞击波)是由于射流的撞击由撞击点产生的波使得液膜剧烈波动破碎[4]。空气动力波和水动力波的发生取决于射流速度、射流撞击角和流动特性(层流或湍流)。空气动力波和水动力波的存在,导致撞击射流雾化的动态演化过程中产生了复杂的射流和液膜的界面破裂行为[5]。对于速度相对较低的层流撞击射流雾化,使用空气动力波的机制可较为准确地描述液膜的破碎,而对于高速或湍流射流则需要引入撞击波的机制来描述这种情况下的撞击射流雾化过程[6-8]。在大多数使用撞击式喷嘴的液体火箭发动机燃烧室中,撞击波主导了雾化过程,因而对于撞击波机制的理解就尤为重要[1]。
针对射流撞击的典型情况,通过高速摄影实验可以记录射流撞击的动态过程,进一步分析包括射流和液膜的形态特征和不同参数的变化规律。随着数值模拟算法的进步,可以获得高精度的界面流动数值模拟[9-12]。在此基础上,进一步建立了各种模型和理论来分析撞击射流的动力学机制[6, 13-15]。但是由于气液界面流动的复杂性,包括气动波和撞击波的耦合作用,不同参数下动力学特征的区别仍有待于进一步研究。
针对复杂的界面流动问题,本征正交分解方法可以有效地识别撞击射流中的主导空间特征,同时可以给出对应模态的时间序列信息,便于分析撞击射流雾化的时空变化[16-17]。此外,通过高速摄影可以获取大量具有高时间分辨率和空间分辨率的实验数据,为使用模态分析技术研究雾化问题提供了条件[18]。本征正交分解在雾化相关的研究中已经有了一定的基础。Arienti等[19]应用本征正交分解方法,研究了横向气流作用下射流雾化过程中的相干结构。其结果表明,在射流分解成大块液体的条件下,可以观察到特定的正交模式的叠加。Chen等[20]采用本征正交分解方法对喷油器喷雾的研究表明,正交分解得到的模态和时间系数清楚地识别了喷雾特性的变化。Dighe等[21]使用本征正交分解方法研究了声场扰动状态下的撞击射流雾化。研究结果表明,当撞击射流是层流时,主要的模态频率等于外部声激发频率,证实了本征正交分解方法解析了雾化过程与声扰动的耦合。
本文通过两个方向的高速摄影获得了撞击射流雾化的动态过程,阐述了不同速度下撞击射流的基本流动模式,使用本征正交分解方法处理图像序列,分析了不同速度下撞击射流的空间和时间特征。该研究通过动态图像序列,提取得到不同速度参数下撞击射流雾化的空间波动特征和频率特征信息,有助于液体火箭发动机雾化结构设计和运行参数的优化,具有一定的工程意义。
图1为实验系统示意图,流体在流量泵的驱动下从注射器推出,经过内径为2 mm的硬质PE管,最后从两个呈一定角度的不锈钢针头喷出,形成两股对撞射流,进一步产生雾化现象。其中硬质PE管通过固定可以减少系统的扰动,不锈钢针头使用内表面粗糙度较小的针头,减小射流的外部扰动。流体驱动使用高精度流量泵(Pump 11 Pico Plus Elite Dual),其优点在于射流速度调节方便,且流量控制精度较高。
实验使用两台高速相机(pco.dimax HS1)从两个方向同步进行拍摄,可以同时对应捕捉液膜的正面和侧面的波动破碎现象,立体地观察撞击射流的空间动态变化过程。为了获得清晰的射流撞击动态过程,采用背光照明对瞬态喷雾过程进行成像,使用了高功率无频闪 LED光源(Model U-100T)进行照明。相机分辨率为1 000像素×562像素,帧率为9 792 帧/s,为了提高成像效果,设置合适的进光量,曝光时间设置为10 μs。
图2给出了实验装置的图片。如图所示,整个实验系统被安装在光学平台上,保证整个实验系统最终光学成像的精度,两个金属针头作为撞击射流的喷口,呈60°夹角被安装在金属框架上,围绕金属框架布置了两台高速相机和两个LED光源,LED光源外部安装了匀光罩,为拍摄提供强度尽量均匀的背景光。实验使用的材料为去离子水,密度为985.2 kg/m3,表面张力为69.66 mN/m,动力黏性系数为1.085 mPa·s。
本征正交分解属于数据驱动的流场模态分解方法,是将原始空间与时间数据分解为空间上的多阶模态(称为本征模态)和各阶模态对应的时间演化系数,各阶模态在空间上相互正交,模态的阶数按照能量的大小由高到低降序排列,能量由本征模态对应的特征值给出。POD方法已经成为一个有效的方法,用来分析液体雾化过程的图像序列。具体对于撞击射流雾化过程而言,POD方法可以针对复杂的气液界面流动过程,识别一个给定正交基函数的统计集合,以获取喷雾过程中的主要空间特征和时间特征,有助于充分认识和解析雾化的内在原理,建立合理的喷雾模型和针对喷雾的控制决策。
下面介绍基于流体高速摄影图像序列的POD方法。通过高速摄影获得一个图像序列,即得到N个实验图像组成的数据集,每个图像均被视为N维空间中的一个向量,图像的强度Ii为向量的大小,具体表现为每个像素点的灰度值。图像序列Ii(ξ,t)可以表示为模态及其相应的时间系数的线性组合,即
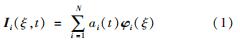
式中:ξ和t分别代表位置变量和时间变量; ai(t)为对应模态的时间系数; φi(ξ)为空间模态或正交特征向量,其在空间中相互正交,表示整个时间序列的空间特征,且
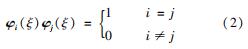
每个POD模态φi(ξ)对于整个图像序列的贡献依据对应模态特征值的大小,特征值以递减的方式排列(λ1>λ2>λ3>…),确定各阶模态的贡献次序。
POD 的处理方法通常有直接POD方法、快照POD方法和基于SVD(奇异值分解)的POD方法。针对大型数据矩阵通常采用后两种方法,快照POD方法和基于SVD的POD方法在实质上是等价的,而基于SVD的方法对图像或是数据序列的舍入误差具有鲁棒性。
针对本实验研究使用POD提取空间模态和时间系数的具体方法,依据矩阵的SVD分解。首先获得不同工况下的实验图像数据,本研究中一组图像数据含有3 000张图片。对于一组图像数据,将单个时刻的数据转换为一个列向量q(ξ),然后叠加不同时刻的数据向量成为一个数据矩阵,即
Y={q(ξ,t1),q(ξ,t2),…,q(ξ,tN)} (3)
使用SVD将式(3)中的数据矩阵Y分解为
Y=USVT (4)
式中:U和V均为正交矩阵; S为对角矩阵。不同的空间模态φi(ξ)可以从矩阵V中读取。时间系数矩阵An为
An=U·Sn (5)
对时间系数矩阵进行傅里叶变换可以给出对应模态的频域信息。模态能量为
Di=S2i (6)
各个模态的能量占比为
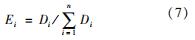
以上的POD方法均在MATLAB里通过自编的代码实现。
基于第1节所描述的撞击射流实验系统,固定撞击角为60°,射流直径为0.26 mm,调节流量泵流量q为15~40 mL/min,对应射流速度uj为4.71~12.56 m/s。撞击射流基本流动模式的变化受到雷诺数和韦伯数的影响,本文中共进行了6个工况的实验,从工况1到工况6射流速度逐渐增加,对应的流动参数在表1中给出。
图3给出了通过两个方向高速摄影得到的5个工况下典型实验图像。根据实验图像展现的流动形态,展开对撞击射流基本流动模式的讨论。图3(a)给出了不同工况下正面拍摄的实验图像。对工况1,两股射流撞击形成一个封闭的液膜,在液膜边缘形成了凸起,这些凸起运动汇集到液膜的下游,最后封闭液膜下方形成一系列断裂的液滴。对于工况2,射流速度增加之后,液膜铺展面积增大,液膜的长宽显著增加。液膜边缘的凸起在汇集的过程中变成指状的液丝,这些液丝在向下运动的过程中断裂成为液滴。工况3表现为破碎的液膜模式,可以发现射流速度相比工况2增加之后,液膜铺展面积进一步增加,可以观察到更多指状液丝的断裂,但是大面积的液膜在空气中运动的过程中无法保持其完整性,液膜下部表面破碎。
工况5为撞击波破碎模式,由撞击点产生了强烈的撞击波,撞击波由撞击点向外径向传播,使得液膜发生剧烈的扰动,液膜沿着波动方向快速地破碎,成为弧状液丝,液丝由于毛细力的作用断裂成为液滴。工况4介于工况3和工况5之间,由于撞击点引发的液膜剧烈扰动,相比工况3的情况出现了更多的指状液丝,液膜下部更早地破碎,与向下运动的指状液丝合并断裂成为液滴,同时液膜从撞击点开始出现的波动表现出了撞击波的模式。
图3(b)为不同工况下侧面拍摄的实验图像,工况1和工况2从侧视图展现了稳定的断裂状态,在工况3的条件下,侧方的扰动开始逐渐增强。在工况4和工况5中,从侧视图可以看出明显的摆动。工况6为撞击波破碎模式下雾化更为完全的工况,从实验图像中可以看到大量的液滴产生,并且粒径更小。
从以上对于流动模式的分析中可以看出,撞击射流雾化过程是在不同的流动参数下表现为一个高度不稳定和动态变化的过程。因此通过一组图片序列识别出涵盖整个时间变化过程的空间特征,将有助于进一步了解其中液膜的波动过程,找出隐藏在时间变化过程中的空间特征,有助于了解相近的工况下射流撞击动态特征的差别。
图4给出了工况5下正面模态分解结果。对于正面拍摄的实验图像,为了POD分析的区域集中于液膜波动破碎的区域,1 000像素×562像素裁剪成为600像素×400像素的区域。对于本文中每一组POD结果,1阶模态有1个颜色标尺,其余高阶模态共用1个颜色标尺。基于2.1节对基本流动模式的分析,工况5对应撞击波的破碎模式。首先显示了一个典型的用于POD处理的实验图像,1阶模态给出了主要的图像波动强度,这里的1阶模态即为平均模态。2阶模态和3阶模态给出了一个在空间中正负交替的空间特征,在模态图像上表示为弧状的等高线,以区分模态特征图像中的正负值区域,显示在这一模态下的空间波动特征。由撞击点产生的撞击波沿撞击平面呈径向传播,波动形状近似椭圆弧状,说明通过基于POD的时间序列分析,2阶模态和3阶模态可以识别撞击波的空间波动特征。从模态图像中还可以发现,在空间的波动随着与撞击点距离加大,有逐渐放大的趋势。在后续的高阶模态,5阶模态展现了更多的交替正负波动特征,10阶模态的图像中则表现了更为复杂的波动干涉特征,100阶模态的图像中已经不能看出整体的空间波动特征,正负值区域呈现零散分布,最后给出的1 000阶模态趋近于数据处理的噪声。
图5给出了工况6下正面模态分解结果,对应于雾化更为完全的撞击波破碎模式。可以发现,模态图像中空间正负分布区域更加集中。
图6给出了工况4下正面模态分解结果。工况4为完全的撞击波破碎模式和液膜破碎模式的混合状态,破碎的液膜在空间大幅度摆动,同时又兼具撞击波的波动。对比工况5和工况4的1阶模态可知,相比工况5撞击波的快速雾化模式,工况4由于液膜破碎,在液膜侧面出现更明显的液丝生长现象,这导致1阶模态整体波动贡献区域分散。2阶模态和3阶模态中大范围的空间正负值变化描述了液膜在空间的摆动过程。4阶模态和5阶模态的空间正负值区域逐渐减小,逐渐显示出正负交替的空间波动特征,这表明其由液膜破碎模式过渡到撞击波的模式。10阶模态则明显表现出了连续正负交替的撞击波模式。以上结果表明POD 的分析对应于工况4,从一个动态图像序列中区分出了液膜摆动破碎模式和撞击波模式的特征。
各阶模态能量由奇异值的平方给出,其大小反映了对应的模态对整个雾化状态的影响和贡献。图7给出了工况5和工况4不同阶数下单个模态的能量,可以发现对于这两个工况,1阶模态占据了大部分能量。这里需要指出的是对于1阶模态,其表现的特征被视为平均模态,其本征模态的特征值比其他模态要大很多,即1阶模态占据了大部分的能量,但是不意味着其他高阶模态对整个撞击射流的贡献低。
对于这一点,Kumar等[22]针对实验结果的POD分析指出,第一模态的特征贡献与选择进行POD分析的原始图像的像素面积成正比,POD应用面积越大,高阶模态的贡献越小。因而更高阶模态对于整个撞击系统的重要性不能完全取决于特征值大小的贡献。除此之外,这些图像本质上对应于三维现象的二维投影。这也可能导致较高模态的特征值较低。
对于图7 中给出的单个模态的能量,除去1阶模态之外,对比2阶模态,工况4表现的能量要高于工况5,即对于工况4,2阶模态代表的大幅度的液膜空间摆动特征对工况4的系统有显著的贡献。图6中给出的典型实验图像和2阶模态图像可以对应说明这一点。对于工况4,3阶模态能量则进一步降低,在后续的模态中,逐步过渡到空间正负交错的撞击波模式。对于工况5,可以发现其2阶和3阶模态对应的能量贡献基本一致,因而可以识别出撞击射流雾化中的完全撞击波模式,在1阶模态之后,可以识别出一组(两个)模态,其特征为在空间中正负交替,对应整个系统中的能量相同,它们对撞击波的模式有显著贡献。
图8给出了工况5和工况4不同阶数累计模态能量,可以发现工况5下在1阶模态的初始能量以及后续的累计模态能量都要高于工况4。这是由于在完全撞击波的模态下,在1阶模态之后,后续的高阶模态都呈现空间交错的模式,直到完全雾化的状态,作用机制明确,模态的能量集中,模态能量快速累积。而工况4下,表现为从液膜破碎到撞击波模式的过渡,通过图6中工况4的POD结果可以明显看出,在过渡状态,单模态的能量较为分散,因而模态能量累积较慢。
依据工况5下2阶模态和3阶模态的时间系数,根据傅里叶变化给出其频域特征信息,之后进一步通过高斯滤波去掉系统识别的杂波扰动,最后给出的频率特征分布信息如图9所示。2阶模态的频率在4.4 kHz左右达到峰值,3阶模态在4 kHz左右达到峰值。
图 10给出了工况5下侧面动态变化,在10.99 m/s的高速射流撞击下,撞击点水动力波波动强烈。撞击波由撞击点向下传递的过程中,振动的幅度不断放大,从侧视图上液片出现了大幅度地摆动。在侧视的动态特征变化中可以发现,液膜在撞击波的作用下表现出了复杂的空间和时间波动特征行为,并没有表现出直观的规律性特征,如在0.5 ms时刻液膜出现了大幅度地折叠,在1.0 ms时刻整个液膜向图像右侧摆动,而在2.5 ms时刻整个液膜则向图像左侧大幅度摆动。
图 11给出了对应工况5下侧面的POD分解结果,典型图像给出了一个用于分解的图像,1 000像素×562像素裁剪成为400像素×210像素的区域。1阶模态给出了侧视的平均流动,整个图像序列的平均流动区域由撞击点向下区域逐渐扩张,这反映了液膜在撞击波作用下波动破碎区域向外发散的过程。2阶模态和3阶模态表现为空间上交错的撞击波模式。仔细观察2阶模态和3阶模态在空间中的分布特征发现,正负值区域相互对应,即2阶模态正值的区域在3阶模态对应位置为负值,在纵向位置上有一定错位。其余高阶模态的特征区域主要表现为液膜在空间中更为复杂的波动行为,4阶模态图像中在下部一侧为正值,一侧为负值,展现了空间特征代表了液膜向一侧摆动的空间特征。5阶模态给出了更为复杂的连续波动,并且其空间波动特征区域更小,小尺寸的区域反映了液膜在空间中更为剧烈和波动幅度更大的行为,如图 10中0.5 ms时刻在空间中折叠的液膜。
图 12给出了对应工况3下侧面的POD分解结果。工况3流动模式为破碎的液膜模式,因而在图 12给出的用于分解的典型图像中可以看到一个完整的液膜区域,该工况下1阶模态图像,即平均模态为同样完整的液膜区域,与工况5相比,1阶模态图像的区域显著减小。对于工况3,破碎的液膜模式对应的高阶模态给出了条状的正负波动区域,长条状的特征区域延伸很长,这表明了在这个图像序列中表现为液膜在破碎过程中分离的液膜向左右两侧的摆动过程。
图 13给出了对应工况1下侧面的POD分解结果,对应的流动模式为从封闭的液膜断裂成一系列的液滴,在典型图像中可以看到侧视的凸起和不稳定的液丝,下一步的趋势要断裂成为液滴。1阶模态的特征接近工况3的工况,在下部平均流动的区域有一定扩张,这是液膜下方波动的液丝。从高阶模态的特征可以看出,侧面在液膜的一系列凸起在模态特征中识别为正负交错的连续空间波动特征,而在下游有凸起合并为液膜则被识别为团状的特征区域。
下面对工况5撞击波机制做进一步地阐释。为了明确工况5下2阶模态和3阶模态在时域上的变化特征,提取了2阶模态和3阶模态的时间系数,进一步进行时域上的平滑滤波,得到了工况5下2阶模态和3阶模态的时间系数变化,如图 14所示。可以发现2阶和3阶模态的时间系数呈现近似相反的变化趋势,2阶模态系数从0时刻开始增长,而3阶模态的时间系数从0时刻开始减小,在2阶模态的时间系数达到一个极大值后,3阶模态的时间系数达到一个极小值,此后的基本变化趋势按照此规律交替往复。在空间上呈现对称特征的2阶模态和3阶模态在时域变化上对工况5下的撞击射流系统表现为相对的贡献,这使得工况5下的撞击波呈现周期性的变化。
图 15(a)和图 15(b)分别给出了工况5下2阶模态和3阶模态的频率,依据时域上的时间系数,根据傅里叶变化给出其频域特征,通过高斯滤波去掉系统识别的杂波扰动,最后给出频率特征分布信息。可以发现工况5下2阶模态和3阶模态幅值均在2 kHz左右达到峰值,这表示2阶和3阶模态具有一致的频域特征,从侧视特征来说,2阶和3阶模态对于工况5下撞击波的波动频率贡献是一致的。
值得注意的是,对于工况5通过正面拍摄和侧面拍摄的图像序列的POD处理,给出的频率特征并不相同。对比图9给出的正视图像2阶和3阶模态的频率信息,可以发现在工况5下,正视图2阶和3阶模态特征频率为侧视图中2阶和3阶模态模态特征频率的2倍。
为了解释这一现象,进一步对比了正视和侧视的模态图像。图 16给出了工况5下正面与侧面的2阶模态图像对比,将正面和侧面获得的2阶模态图像依据比例放缩到相同的尺寸,并且将正视和侧视的撞击点平齐。从对比图像可以看出,正视模态图像中2个正负空间波动特征对应侧视图中的1个正负空间波动特征,图中3条黑色虚线划分的区域表明了这一现象。这是由于在正视图像中撞击波空间波动特征中,波峰和波谷在图像中均被识别为峰值,而在侧视图像中,侧视的波动可以区分波峰和波动的特征,识别为一个空间波动,因而在正视图像中识别的特征频率是侧视图像对应频率的2倍。
图 16 工况5下正面与侧面的2阶模态对比
Fig.16 Comparison of the 2nd order mode between the front and the side at case 5
这里指出,这一结论仅对应于撞击波破碎模式,是由于不同方向高速摄影图像中对于撞击波的波动特征的识别不同导致的,对于其他非单一撞击波破碎模式的工况并不适用,包括撞击波-液膜破碎混合模式。
在正视图像序列的POD结果中,高阶模态特征频率的1/2即为该阶模态特征对应的波动频率。这一结论对于高速撞击射流喷雾,特别是密集喷雾的动态图像序列分析有显著价值。在密集的喷雾中,侧视图像包含了大量的雾化液滴,从成像上很难识别液膜的波动,这样通过正视图形模态特征频率的1/2,就可以得出对应模态特征液膜波动的频率。
本文通过高速摄影,使用本征正交分解方法,研究了撞击射流动态变化过程中的空间和时间特征,得到的主要结论如下。
1)通过不同流速下撞击射流的实验结果,阐明了不同工况下的基本流动模式。
2)正视图像序列的模态分解结果区分了撞击波模式和撞击波-液膜破碎混合模式的空间特征,撞击波模式各模态能量更高。
3)侧视图像序列的模态分解结果依次给出了侧视撞击波特征、液膜破碎特征和液膜上液滴断裂特征,在撞击波模式下一组相对高阶模态的时间系数具有反向变化的趋势,正视图模态特征频率为侧视图对应频率的2倍。
综上,本文将基于奇异值分解的本征正交分解方法应用于不同工况下撞击射流雾化的图像序列测试分析,提取空间中的波动特征和频域上对应的频率特征信息,有助于加深对于撞击射流雾化内在机制的理解,获得的相关特征信息有助于优化液体火箭发动机雾化结构设计和运行参数。