作者简介:李欣(1987—),男,博士,工程师,研究领域为空间运输系统,火箭发动机
(1. 北京宇航系统工程研究所, 北京 100076;2. 北京航空航天大学 宇航学院, 北京 100191;3. 中国运载火箭技术研究院, 北京 100076)
(1. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China;2. School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;3. China Academy of Launch Vehicle Technology, Beijing 100076, China)
variable-pitch inducer; cavitation performance; synchronous rotating cavitation; visualization
备注
作者简介:李欣(1987—),男,博士,工程师,研究领域为空间运输系统,火箭发动机
为了研究变螺距诱导轮的气蚀性能,通过试验观察了变螺距诱导轮的气蚀发展变化情况,分析了其内部的压力脉动现象。结果 表明:诱导轮内的气穴随着入口压力降低,会呈现不同的气穴形态;气穴发展受流量影响,流量越大,气穴发展速度越快;诱导轮内发生了同步旋转气蚀,同步旋转气蚀也受流量影响,流量越大,同步旋转气蚀越强。
In order to study cavitation performance of the variable-pitch inducer, the cavitation development and variation of the variable-pitch inducer were observed, and the pressure pulsation phenomenon in the inducer was investigated. The results show that the different cavitation shapes appear in cavitation in the inducer with inlet pressure decreasing, flow rate has an effect on cavitation development, which means that the cavitation develops faster at higher flow rate, synchronous rotating cavitation appears in the inducer, and the higher the flow rate is, the more serious the synchronous rotating cavitation becomes.
引言
诱导轮是安装在离心泵前的轴流泵,它的作用是为离心泵增压,避免离心泵发生气蚀。在火箭动力系统中,为了减轻贮箱重量,诱导轮入口压力通常较低,受工况变化以及一些干扰因素的影响,可能会产生严重的气蚀,导致诱导轮流道被堵塞,从而使泵的扬程迅速下降。在某些工况下,还会发生气蚀不稳定现象,如旋转气蚀[1-3]、气蚀喘振等[4],引起轴振动,进而对轴承和密封等零部件的可靠性造成威胁,影响泵的重复使用。
国外通过试验和数值仿真对气蚀不稳定现象开展了大量研究。2005年,Fuji等通过试验发现,在诱导轮入口增加喷射流,当喷射流量为总流量的10%,并且射流方向与旋转方向一致时能够有效抑制气蚀不稳定现象[5]。2006年,Hosangadi等使用CHUNCH软件比较了诱导轮在液氢和水中的性能,发现热力学效应的存在能够改善诱导轮的气蚀性能[6]。2008年,Kim等研究了在诱导轮上游安装环形挡板对气蚀喘振的影响,发现其对气蚀喘振有很好的抑制作用,但是对诱导轮的抽吸性能和压升影响不大,特别是在低流量下[7]。2011年,Iga等采用二维平面叶栅模型对三叶片诱导轮气蚀喘振现象进行了数值模拟分析,根据流场及喘振的特点,他们将气蚀喘振分为三类:第一类喘振由小的旋涡气蚀和大尺度的脉动组成,第二类喘振由具有射流结构的层状气蚀组成,第三类喘振由伴随有脉动特性的次同步旋转气蚀组成[8]。2012年,韩国的Lee等研究了一个两叶片两级式诱导轮的气蚀性能,发现两级式诱导轮与传统的单级式诱导轮相比对气蚀喘振和不对称气蚀等气蚀不稳定现象有较好的抑制作用[9]。通过数值模拟和实验研究相结合的方法,发现两级式诱导轮能抑制气蚀不稳定的原因是第一级诱导轮的存在使得第二级诱导轮叶片前缘的气穴形状发生了改变。2014年,Pace等针对在CPRTF做过试验的三叶片诱导轮,研究了几何条件对气蚀流动不稳定的影响[10]。根据上面的研究可以发现,国外主要研究气蚀不稳定现象的产生机理及抑制方法,但是并没有形成统一的设计准则。
近几年,国内围绕气蚀不稳定现象也开展了一些研究。2009年,陈晖等通过数值模拟诱导轮二维叶栅中的非定常流动,研究了旋转气蚀,并对其机理进行了分析[11]。2013年,唐飞等利用CFD方法分析了阶梯壳体和叶片打孔对诱导轮气蚀性能的影响[12]。2014年,叶汉玉等通过数值模拟捕捉到了旋转气蚀现象,发现气穴尺寸变化与攻角存在一定的关系[13]。2015年,Li等搭建了诱导轮气蚀性能试验台,研究了叶尖间隙对诱导轮气蚀性能的影响。通过增大叶尖间隙,有效抑制了同步旋转气蚀[14]。
本文以一个变螺距诱导轮为研究对象,通过可视化试验研究了气穴在不同流量下的发展变化规律,同时采用FFT(Fast Fourier Transformation)方法对诱导轮的脉动压力进行了分析。
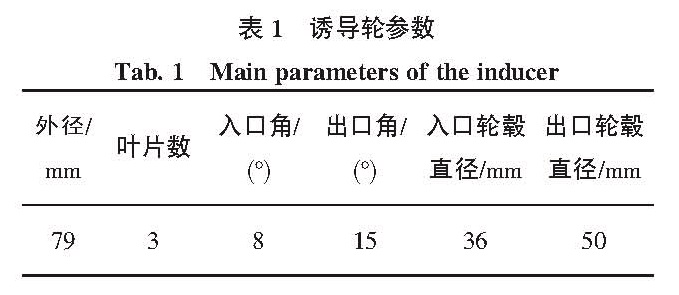
1 研究对象
2 试验方法
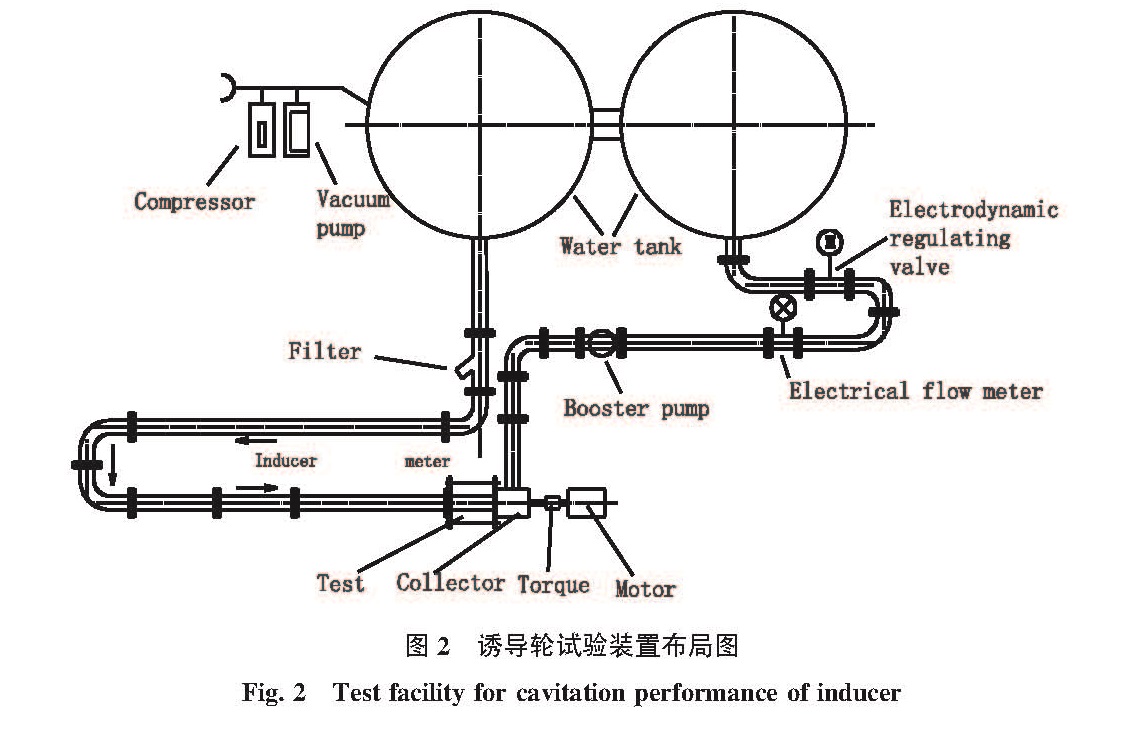
诱导轮试验装置布局如图2。整个试验台为闭式试验系统,采用水作为试验工质。试验时,采用真空泵和压气机来调节诱导轮入口压力。试验诱导轮由变频电机驱动,最大转速可达6 000 rpm。诱导轮流量通过电动调节阀进行控制。在诱导轮和调节阀之间装有辅助泵,当流量不足时,通过辅助泵来克服管路流阻损失,提高系统流量。
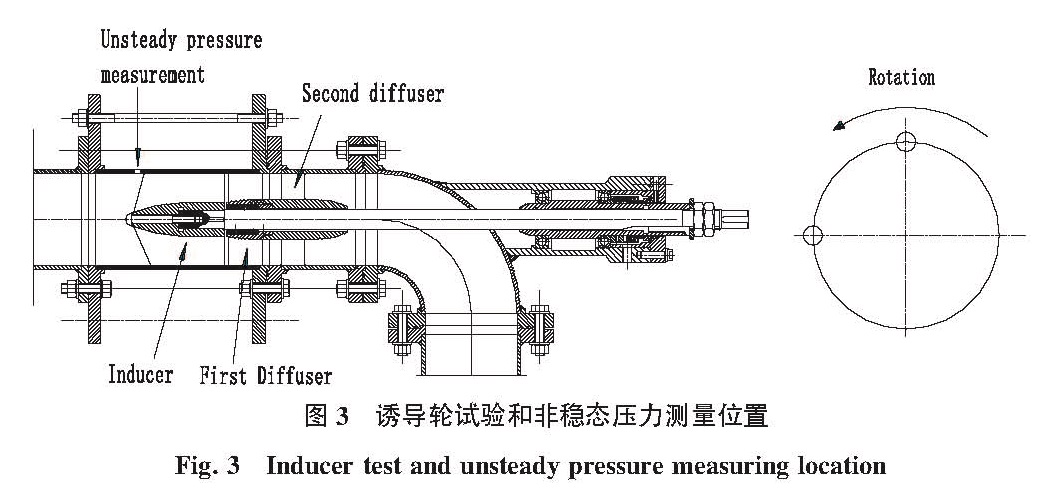
为了观察诱导轮内部流动状态,采用有机玻璃加工诱导轮透明壳体。两个溅射薄膜压力传感器(型号:CYB-20S;量程:-0.1~0.7 MPa,精度:0.5%)分别安装在诱导轮入口和出口,用来测量诱导轮入口压力和出口压力。另有两个同类型的压力传感器(型号:CYB-20S;量程:-0.1~1 MPa,精度:0.5%)安装在透明壳体上用来测量压力脉动。为了不影响流场,传感器的头部与壳体齐平安装。两个传感器沿旋转方向间隔90度,轴向位置在诱导轮叶片前缘附近,因为由气蚀不稳定引起的压力脉动在叶片前缘附近最明显。试验数据采样频率设为1 600 Hz,并且持续4 s。试验时流量通过电磁流量计测量。
3 试验结果与分析
4 结论
通过试验研究了变螺距诱导轮的气蚀性能,包括气蚀发展变化规律和气蚀不稳定现象,得到以下结论:
1)随着气蚀数降低,诱导轮内的气蚀流动在发展过程中会出现不同的形态,包括轮缘漩涡气穴、叶面气穴和回流涡气穴等,其中叶面气穴是造成诱导轮流道喉部堵塞的主要原因。
2)流量会对诱导轮气蚀流动产生影响,流量越大,初生气蚀数越小,但是气穴发展更快,临界气蚀数比小流量下大。
3)同步旋转气蚀受流量影响,流量越大,同步旋转气蚀越强,1.1Qd工况下同步旋转气蚀引起的压力脉动幅值为0.8Qd工况下的1.62倍。
诱导轮的流量、入口压力和扬程分别用无量纲数流量系数、气蚀数和扬程系数表示。

式中:Φ为流量系数;σ为气蚀数;Ψ为扬程系数;Ω为转速,rad/s;rT为诱导轮叶尖直径,m;Q为体积流量,m3/s;pv为介质的饱和蒸汽压,Pa;p1为诱导轮入口静压,Pa;ρ为介质密度,kg/m3;p2为诱导轮出口静压,Pa。
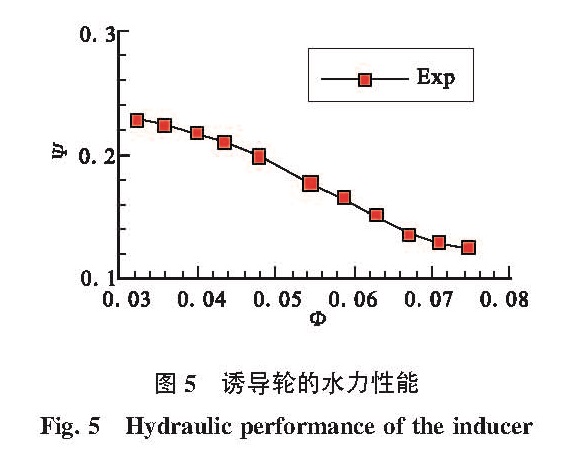
3.1 水力性能试验结果诱导轮的水力性能试验结果见图5,图中横坐标为流量系数Φ,纵坐标为扬程系数Ψ。可以看出,随着流量增加,诱导轮扬程逐渐降低,并且扬程随流量基本呈线性变化。由于在整条曲线上不存在斜率是正值的流量区域,故诱导轮不会发生旋转失速,同时可以认为该诱导轮在试验的流量区域能够稳定工作[15]。
3.2 气蚀性能试验结果图6是两级诱导轮的气蚀性能曲线。从图中可以明显看出,在诱导轮扬程发生10%陡降前,诱导轮扬程成阶梯下降,且不同工况下其扬程下降量不同。在设计流量Qd下,阶梯处扬程下降量为2.3%,0.8Qd和1.1Qd流量工况下扬程下降量分别为1.8%和4.9%。在国外文献中也出现过这种阶梯式下降的气蚀性能曲线,在台阶处都发生了气蚀不稳定现象[16-17]。
随着流量减小,诱导轮的扬程逐渐升高,气蚀性能也存在差异。把诱导轮扬程发生10%陡降时的气蚀数定义为临界气蚀数,在不同的流量下,诱导轮的临界气蚀数σ10%不相等。在设计流量Qd和1.1Qd工况下临界气蚀数σ10%分别为0.038 9和0.055 4,而0.8Qd工况下,当气蚀数降低到试验的最小值0.034 1时,扬程下降了9.1%,未达到临界状态,即随着流量增大,诱导轮的气蚀性能逐渐变差。因为小流量下,诱导轮回流更强,改变了诱导轮入口的流动情况,从而改善了诱导轮的气蚀性能,但是回流增强也会增大流动损失,导致诱导轮的效率下降。
3.2.1 诱导轮气蚀流动可视化结果分析通过可视化试验,观察了诱导轮内部的气蚀流动发展变化情况。设计流量Qd下气蚀流动随气蚀数变化情况见图7。当气蚀数σ=0.422 1时,诱导轮开始产生气穴。气穴首先出现在诱导轮叶片吸力面前缘与轮缘交界处,此处圆周速度最大,静压最低,同时由于压力面和吸力面存在压差,在叶尖间隙处会产生轮缘漩涡,导致该处最容易产生气穴。此时的气穴呈细长的漩涡状,称作轮缘漩涡气穴[15],见图7(a)。随着气蚀数减小,即入口压力的降低,气穴区域逐渐增大。在气蚀数从0.422 1减小到0.136 6的过程中,轮缘漩涡气穴逐渐变粗变长,见图7(b)至图7(d)。由于叶尖间隙处存在回流,故气穴在回流作用下,与叶片始终保持一定的角度。当气蚀数降低到0.085 4时,轮缘漩涡气穴继续增大,并且开始附着在叶片上,此时的气穴称为叶面气穴,如图7(e)。由于气穴区域受离心力的影响,主要集中在叶片吸力面轮缘附近,并没有对主流造成影响,故诱导轮的扬程并没有降低。当气蚀数继续减小到0.034 1时,此时的气穴已经发展成为片状的叶面气穴,并且开始堵塞流道喉部,见图8(f),于是导致诱导轮扬程下降。
同一气蚀数下,气穴区域是不稳定的,气穴形状时刻在发生变化,见图8。此时气穴虽然没有导致扬程降低,但是因为气穴形态的变化,也会引起振动等不稳定现象。
图7 设计流量Qd气蚀流动随气蚀数发展变化情况
Fig.7 Variation of cavitation flow in inducer with different cavitation numbers at design flow Qd图8 设计流量Qd下σ=0.136 6时不同时刻气穴形态
Fig.8 Cavitation shapes at different moment and at design flow Qd,as σ=0.136 61.1Qd和0.8Qd工况下气蚀流动随气蚀数变化情况与设计流量Qd下类似,气穴在不同流量的发展过程大致如下:首先在诱导轮吸力面前缘和轮缘交界处出现轮缘漩涡气穴,随着气蚀数减小,气穴发展为叶面气穴,并且在主流和回流交界处生成回流涡气穴,随后内部多种气穴共同发展,最终叶面气穴堵塞流道喉部,导致扬程下降。
诱导轮的流量会对气蚀流动的发展产生影响,不同流量下诱导轮的初生气蚀数见表2。可见,随着流量增大,初生气蚀数逐渐减小,但是从图6看出,临界气蚀数却随着流量增大而增大。由此可知,不同流量下,气穴的成长速度不一样。在大流量工况下,气蚀从初生到堵塞流道的气蚀数变化范围比小流量工况小,即大流量工况下,气穴成长的速度较快。
试验中还观察到,在气蚀数降低到临界气蚀数之前,诱导轮压力面也出现了气蚀,见图9。这是因为诱导轮是变轮毂诱导轮,从入口到出口,轮毂直径逐渐增大,使得流道面积逐渐减小。当诱导轮在1.1Qd工况下工作时,攻角比设计流量Qd下小,又因为回流和轮毂形状的共同作用,故在诱导轮入口局部区域出现负攻角,导致压力面发生气蚀。
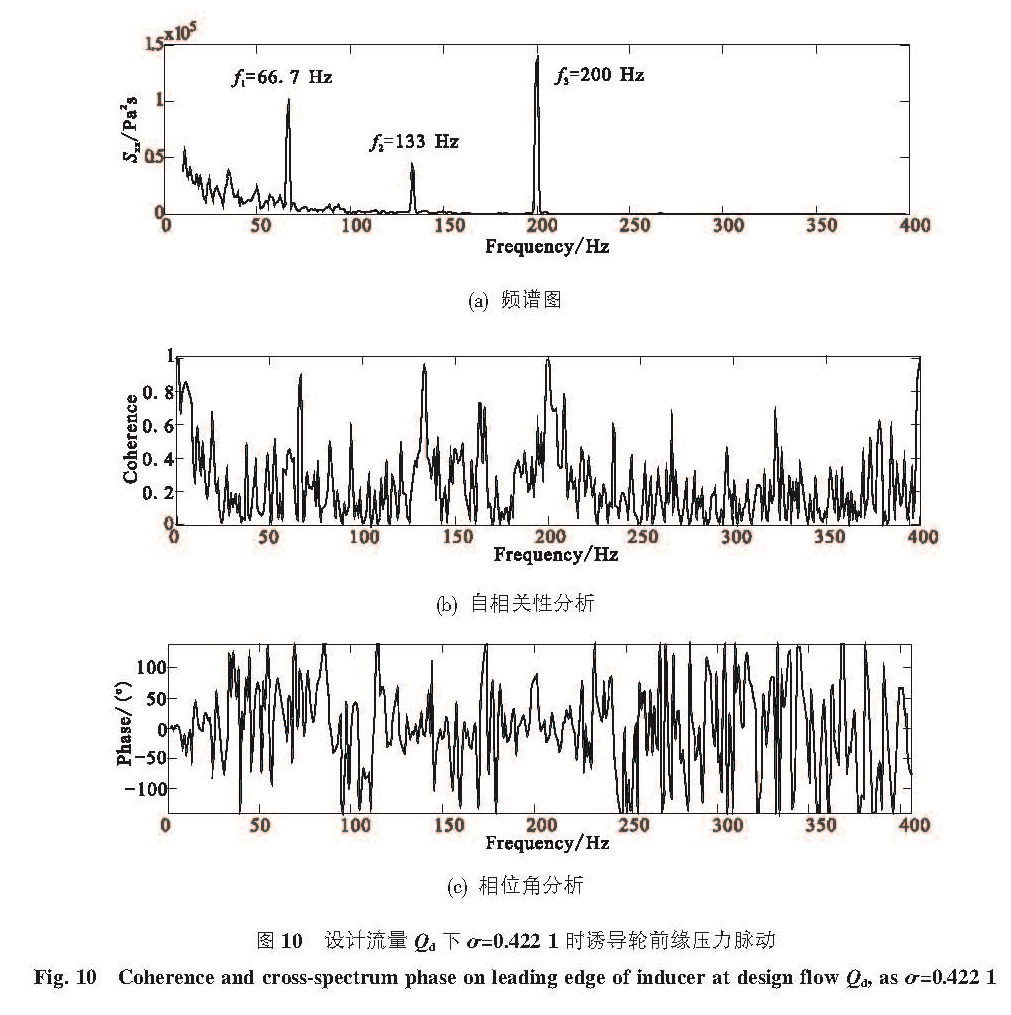
3.2.2 诱导轮气蚀不稳定现象研究设计流量Qd下,气蚀数σ=0.422 1时诱导轮前缘压力脉动见图 10,存在频率f1=66.7 Hz,f2=133 Hz和f3=200 Hz的压力脉动。因为诱导轮刚开始气蚀,故此时的压力脉动并不是因为气蚀引起的。对信号进行自相关性分析和相位角分析,结果见图 10(b)和10(c),三个峰值的压力脉动的相关性都大于0.9,f1和f2的相位角差均为0°,f3的相位角差为90°,而诱导轮的转频fN=66.7 Hz,由此可知,f1为轴转动引起的压力脉动,f3为叶片转动引起的压力脉动。而频率f2=f3-f1,满足后面的关系式[17],可知为轴转动与叶片转动的耦合作用引起的。
φ(f)=aφ(f3)-bφ(f1)
式中a和b为整数。
图 10 设计流量Qd下σ=0.422 1 时诱导轮前缘压力脉动
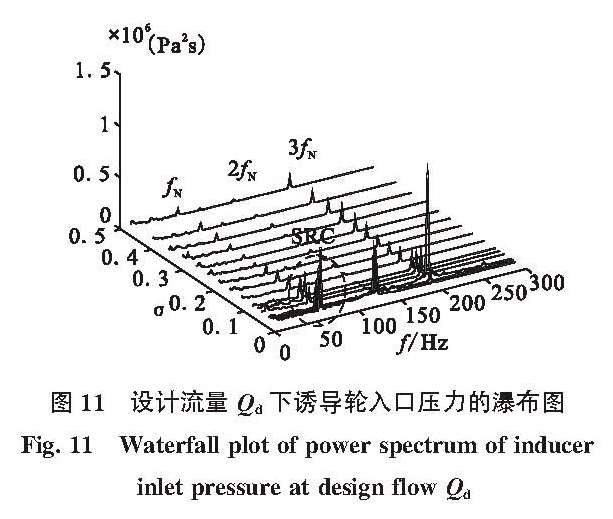
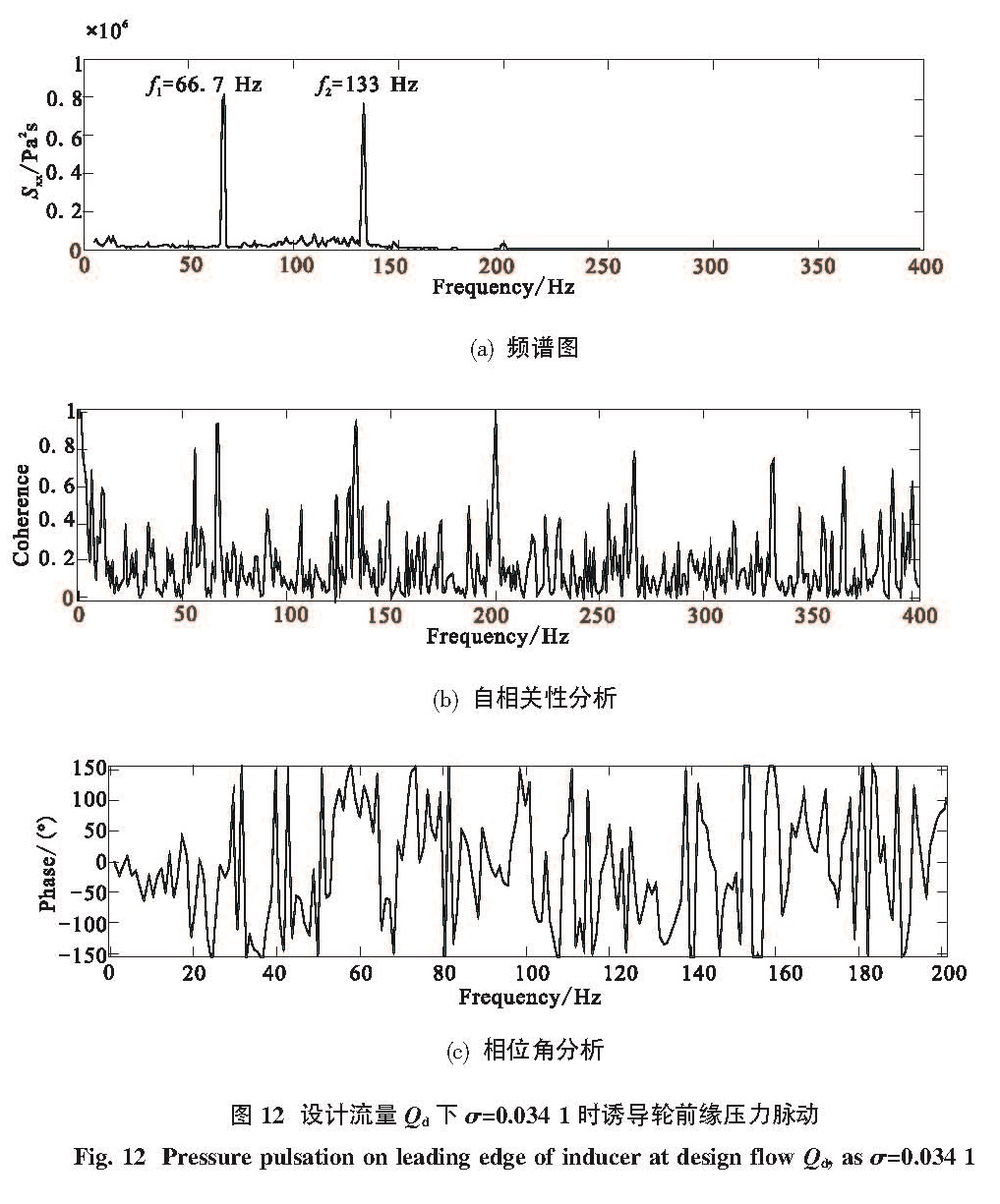
Fig.10 Coherence and cross-spectrum phase on leading edge of inducer at design flow Qd, as σ=0.422 1图 11是设计流量Qd下诱导轮前缘压力脉动的瀑布图。图中坐标分别是压力的功率谱密度、气蚀数和频率。在试验中主要存在三种压力脉动,其频率分别为fN,2fN和3fN。从图中看出,当气蚀数σ=0.1时,叶频引起的压力脉动开始增大,这是因为压力测点附近开始发生气蚀,导致压力脉动增强,随着气蚀数减小,气蚀范围增大,脉动幅值也不断增大,当增大到最大值时,由于压力测点附近全部气蚀,此时测点周围的压力都是饱和蒸汽压,导致该压力脉动迅速减小。轴频引起的压力脉动fN随着气蚀数减小也在增大。当σ=0.034 1时,压力脉动达到最大值。该工况下诱导轮前缘的压力脉动见图 12。此时频率等于转频fN的幅值的功率谱密度增大了一个数量级,相位角差约为-90°,可知旋转单元体数目为1,脉动沿径向传播,因此该峰值是由于诱导轮内部发生同步旋转气蚀现象引起的。
图 11 设计流量 Qd下诱导轮入口压力的瀑布图
Fig.11 Waterfall plot of power spectrum of inducer inlet pressure at design flow Qd图 12 设计流量Qd 下σ=0.034 1 时诱导轮前缘压力脉动
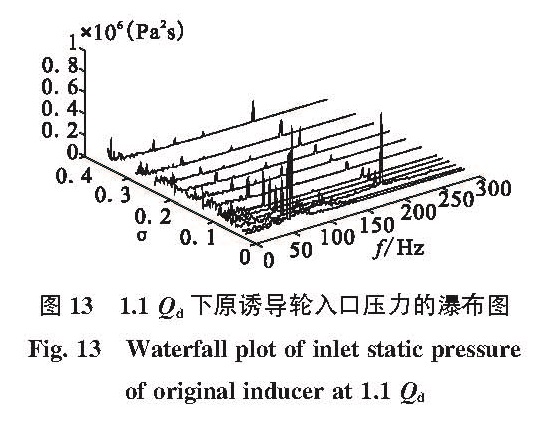
Fig.12 Pressure pulsation on leading edge of inducer at design flow Qd, as σ=0.034 1图 13和图 14是1.1Qd和0.8Qd工况下诱导轮前缘压力脉动的瀑布图。从图中可以看出,这两种流量下诱导轮也发生了同步旋转气蚀。
图 13 1.1 Qd下原诱导轮入口压力的瀑布图
Fig.13 Waterfall plot of inlet static pressure of original inducer at 1.1 Qd图 14 0.8 Qd下原诱导轮入口压力的瀑布图
Fig.14 Waterfall plot of inlet static pressure of original inducer at 0.8 Qd不同流量下,同步旋转气蚀引起的压力脉动的最大幅值见表3。从表中可以看出,随着流量增大,同步旋转气蚀引起压力脉动的最大幅值也显著增大,1.1Qd工况下的最大幅值是0.8Qd工况下的1.62倍,说明大流量下的同步旋转气蚀更应该引起重视。
- [1]TSUJIMOTO Y, KAMIJO K, YOSHIDA Y. A theoretical analysis of rotating cavitation in inducers[J]. Journal of fluids engineering, 1993, 115: 135-141.
- [2]TSUJIMOTO Y, YOSHIDA Y, MAEKAWA Y, et al. Observations of oscillating cavitation of an inducer[J]. Journal of fluid engineering, 1997, 119: 775-781.
- [3]HASHIMOTO T, YAMADA H, FUNATSU S, et al. Rotating cavitation in three and four-bladed inducers: AIAA-1997- 3026[R]. Reston: AIAA, 1997.
- [4]FURUKAWA A, ISHIZAKA K, WATANABE S. Flow measurement in helical inducer and estimate of fluctuating blade force in cavitation surge phenomena[J]. JSME international journal, 2002, 45(3): 672-677.
- [5]FUJI A, MIZUNO S, HORIGUCHI H, et al. Suppression of cavitation instabilities by jet injection at inducer inlet [C]//2005 ASME Fluids Engineering Division Summer Meeting and Exhibition. Houston, TX, USA: ASME, 2005.
- [6]HOSANGADI A, AHUJA V, UNGEWITTER R J, et al. Numerical study of a flat plate inducer comparison of performance in liquid hydrogen and water[C]//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Sacramento, California: [s.n.], 2006: 111-118.
- [7]KIM J, ISHIZAKA K, ISHIZAKI M, et al. Suppression effect of upstream installed ring-shaped obstacle plate on cavitation surge in pump inducers[J]. Journal of fluid science and technology, 2008, 3(1): 1-10.
- [8] IGA Y, Hashizume K, YOSHIDA Y. Numerical Analysis of Three Types of Cavitation Surge in Cascade[J]. Journal of fluids engineering. 2011. 133: 071102-1-071102-13
- [9] LEE K, CHOI J, KANG S. Study on the suppression of cavitation instabilityin a two-stage inducer[J]. Journal of propulsion and power, 2012, 28(5): 946-954.
- [10] PACE G, VALENTINI D, PASINI A, et al. Geometry effects on flow instabilities of different three-bladed inducers[J]. Journal of fluids engineering, 2015, 137:041304-1-041304-12.
- [11] 陈晖, 李斌, 张恩昭, 等. 液体火箭发动机高转速诱导轮旋转气蚀[J]. 推进技术, 2009, 30(4): 390-395.
- [12] 唐飞, 李家文, 李永, 等. 提高液体火箭发动机诱导轮汽蚀性能的研究[J]. 火箭推进, 2013, 39(3): 44-49,57. TANG Fei, LI Jiawen, LI Yong, et al. Study on improving cavitation performance of inducer for liquid rocket engine[J]. Journal of rocket propulsion, 2013, 39(3): 44-49, 57.
- [13] 叶汉玉, 李家文, 李欣. 诱导轮旋转汽蚀数值模拟[J]. 火箭推进, 2014, 40(4): 43-49. YE Hanyu, LI Jiawen, LI Xin. Numerical simulations of rotating cavitation in inducer[J]. Journal of rocket propulsion,2014, 40(4): 43-49.
- [14] LI X, LI J,WANG J, et al. Study on cavitation instabilities in a three-bladed inducer[J]. Journal of propulsion and power, 2015, 31(4): 1051-1056.
- [15] BRENNEN C E. Hydrodynamic of pumps [M]. England:Cambridge University Press, 1994.
- [16] LEE K, YOO J, KANG S. Experiments on cavitation instability of a two-bladed turbopump inducer[J]. Journal of maechanical science and technology, 2009(23): 2350-2356.
- [17] TORRE L, PASINI A, CERVONE A, et al. Effect of tip clearance on the performance of a three-bladed axial inducer[J]. Journal of propulsion and power, 2011, 27(4): 890-898.